W tej sekcji omówiono reguły wnioskowania, które można zastosować w celu uzyskania dowodu — łańcucha wniosków prowadzących do pożądanego celu. Najbardziej znana reguła nazywa się Modus Ponens (łac. tryb, który potwierdza) i jest zapisana:
α⇒β , α / β
Notacja oznacza, że ilekroć podane są jakiekolwiek zdania postaci α ⇒ β i α są dane, to zdanie β można wywnioskować. Na przykład, jeśli (WumpusAhead ∧ WumpusAlive) ⇒ Shoot i (WumpusAhead ∧WumpusAlive) można wywnioskować Shoot. Inną przydatną regułą wnioskowania jest I-Eliminacja, która mówi, że z koniunkcji można wywnioskować dowolną z koniunkcji:
α Λ β / α
Na przykład z(WumpusAhead ∧WumpusAlive) , WumpusAlive można wywnioskować. Rozważając możliwe wartości prawdy α i β, można łatwo wykazać raz na zawsze, że Modus Ponens i And-Elimination są słuszne. Reguły te mogą być następnie stosowane w dowolnych konkretnych przypadkach, w których mają zastosowanie, generując solidne wnioskowania bez konieczności wyliczania modeli. Wszystkie logiczne równoważności mogą być użyte jako reguły wnioskowania. Na przykład równoważność dwuwarunkowej eliminacji daje dwie reguły wnioskowania
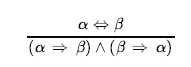
i
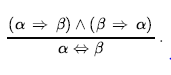
Nie wszystkie reguły wnioskowania działają w obu kierunkach. Na przykład nie możemy uruchomić Modus Ponens w przeciwnym kierunku, aby uzyskać α ⇒ β i α z β. Zobaczmy, jak te reguły wnioskowania i równoważności można wykorzystać w świecie wumpusa. Zaczynamy od bazy wiedzy zawierającej R1 poprzez R5 i pokazujemy jak udowodnić ¬P1,2, czyli nie ma dołu w [1,2]:
- Zastosuj dwuwarunkową eliminację R2, aby uzyskać
![]()
- Zastosuj I –Eeliminację R6, aby uzyskać
![]()
- Logiczna równoważność dla przeciwstawnych daje
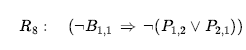
- Zastosuj Modus Ponens za pomocą R8 i percept R4 (tj. ¬B1,2 ), aby uzyskać
![]()
- Zastosuj regułę De Morgana, podając wniosek
![]()
Oznacza to, że ani [1,2] ani [2,1] nie zawiera dołu.
Każdy z algorytmów wyszukiwania w Rozdziale 3 może być użyty do znalezienia sekwencji kroków, która stanowi dowód taki jak ten. Wystarczy zdefiniować problem dowodowy w następujący sposób:
STAN POCZĄTKOWY: początkowa baza wiedzy.
AKCJE: zestaw akcji składa się ze wszystkich reguł wnioskowania zastosowanych do wszystkich zdań, które pasują do górnej połowy reguły wnioskowania.
WYNIK: wynikiem działania jest dodanie zdania w dolnej połowie reguły wnioskowania.
CEL: cel to stan, który zawiera zdanie, które próbujemy wędrować.
Poszukiwanie dowodów jest więc alternatywą dla wyliczania modeli. W wielu praktycznych przypadkach znalezienie dowodu może być bardziej efektywne, ponieważ dowód może zignorować nieistotne twierdzenia, bez względu na to, ile ich jest. Na przykład dowód przed chwilą prowadzący do ¬P1,2 Λ ¬P2,1 nie wspomina o zdaniach B2,1, P1,1, P2,2 lub P3,1. Można je zignorować, ponieważ zdanie celu, P1,2 , pojawia się tylko w zdaniu R2 ; pojawiają się tylko w R4 i R2 tak więc R1, R3 i R5 nie mają wpływu na dowód. To samo miałoby miejsce, nawet gdybyśmy dodali milion zdań do bazy wiedzy; z drugiej strony prosty algorytm tabeli prawdy zostałby przytłoczony wykładniczą eksplozją modeli. Ostatnią właściwością systemów logicznych jest monotoniczność, która mówi, że zbiór zdań pociągających za sobą może się powiększać tylko w miarę dodawania informacji do bazy wiedzy. Dla dowolnych zdań α i β,
![]()
Załóżmy na przykład, że baza wiedzy zawiera dodatkowe twierdzenie β stwierdzające, że na świecie jest dokładnie osiem dołów. Ta wiedza może pomóc agentowi wyciągnąć dodatkowe wnioski, ale nie może unieważnić żadnego wniosku, który został już wywnioskowany przez α – takiego jak wniosek, że nie ma dołków w [1,2]. Monotoniczność oznacza, że reguły wnioskowania mogą być stosowane zawsze, gdy w bazie wiedzy zostaną znalezione odpowiednie przesłanki – wniosek z reguły musi nastąpić niezależnie od tego, co jeszcze znajduje się w bazie wiedzy.