Ta sekcja podsumowuje podstawowe koncepcje logicznej reprezentacji i rozumowania. Te piękne idee są niezależne od jakiejkolwiek szczególnej formy logiki. Dlatego odkładamy szczegóły techniczne tych form do następnej sekcji, używając zamiast tego znanego przykładu zwykłej arytmetyki. W sekcji 7.1 powiedzieliśmy, że bazy wiedzy składają się ze zdań. Zdania te są wyrażane zgodnie ze składnią języka reprezentacji, który określa wszystkie poprawnie sformułowane zdania. Pojęcie składni jest wystarczająco jasne w zwykłej arytmetyce: „x + t = 4” to zdanie dobrze uformowane, podczas gdy „x4y + =” nie. Logika musi również określać semantykę lub znaczenie zdań. Semantyka określa prawdziwość każdego zdania w odniesieniu do każdego możliwego świata. Na przykład semantyka arytmetyki określa, że zdanie „x + y = 4 ” jest prawdziwe w świecie, w którym x wynosi 2, a y wynosi 2, ale fałszywe w świecie, w którym x wynosi 1, a y wynosi 1. W standardowej logice każde zdanie musi być prawdziwe lub fałszywe w każdym możliwym świecie – nie ma „pomiędzy”. Kiedy musimy być precyzyjni, zamiast „świata możliwego” używamy terminu model. Podczas gdy możliwe światy mogą być traktowane jako (potencjalnie) rzeczywiste środowiska, w których podmiot może się znajdować lub nie, modele są matematycznymi abstrakcjami, z których każda ma ustaloną wartość prawdy (prawda lub fałsz) dla każdego odpowiedniego zdania. Nieformalnie możemy myśleć o świecie możliwym jako na przykład, gdy mężczyźni i kobiety siedzą przy stole grając w brydża, a zdanie x + y = 4 jest prawdziwe, gdy w sumie są cztery osoby. Formalnie możliwe modele są po prostu wszystkimi możliwymi przypisaniami nieujemnych liczb całkowitych do zmiennych x i y. Każde takie przypisanie określa prawdziwość każdego zdania arytmetycznego, którego zmiennymi są x i y . Jeśli zdanie α jest prawdziwe w modelu m , mówimy , że m spełnia alfa lub czasami m jest modelem α . Używamy notacji M(α) do oznaczenia zbioru wszystkich modeli . Teraz, gdy mamy pojęcie prawdy, jesteśmy gotowi porozmawiać o logicznym rozumowaniu. Wiąże się to z relacją logicznego wynikania między zdaniami – ideą, że zdanie logicznie wynika z innego zdania. W notacji matematycznej piszemy
α |= β
oznaczać, że zdanie α pociąga za sobą zdanie β . Formalna definicja implikacji jest następująca: wtedy i tylko wtedy, gdy w każdym modelu, w którym α jest prawdziwa, β jest również prawdziwa. Używając właśnie wprowadzonej notacji, możemy zapisać
![]()
(Zwróć uwagę na kierunek tutaj ⊆: jeśli , to alfa jest silniejszym stwierdzeniem niż beta: wyklucza więcej możliwych światów.) Relacja wynikania jest znana z arytmetyki; cieszy nas pomysł, że zdanie x = 0 pociąga za sobą zdanie xy = 0 . Oczywiście w każdym modelu, w którym x wynosi zero, jest tak, że xy wynosi zero (niezależnie od wartości y ). Możemy zastosować ten sam rodzaj analizy do przykładu rozumowania wumpus-world podanego w poprzedniej sekcji. Rozważ sytuację na rysunku (b): agent wykrył nic w [1,1] i powiew w [2,1]. Te spostrzeżenia, w połączeniu z wiedzą agenta o regułach świata wumpusa, tworzą KB. Agenta interesuje, czy sąsiednie kwadraty [1,2], [2,2] i [3,1] zawierają doły. Każdy z trzech kwadratów może, ale nie musi, zawierać dołek, więc (pomijając na razie inne aspekty świata) mamy 23 = 8 możliwych modeli. Te osiem modeli pokazano na rysunku
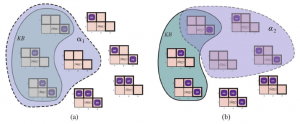
KB można traktować jako zbiór zdań lub jako pojedyncze zdanie, które potwierdza wszystkie poszczególne zdania. KB jest fałszywe w modelach, które są sprzeczne z tym, co wie agent – na przykład KB jest fałszywe w każdym modelu, w którym [1,2] zawiera dół, ponieważ nie ma wiatru w [1,1]. W rzeczywistości istnieją tylko trzy modele, w których KB jest prawdziwe, a na rysunku są one otoczone linią ciągłą. Rozważmy teraz dwa możliwe wnioski:
![]()
KB można traktować jako zbiór zdań lub jako pojedyncze zdanie, które potwierdza wszystkie poszczególne zdania. KB jest fałszywe w modelach, które są sprzeczne z tym, co wie agent — na przykład KB jest fałszywe w każdym modelu, w którym [1,2] zawiera dół, ponieważ nie ma wiatru w [1,1]. W rzeczywistości istnieją tylko trzy modele, w których KB jest prawdziwe i są one otoczone linią ciągłą na rysunku 7.5. Rozważmy teraz dwa możliwe wnioski:
Modele α1 i α2 otoczyliśmy liniami kropkowanymi odpowiednio na rysunkach (a) i (b). Po inspekcji widzimy, co następuje:
w każdym modelu, w którym KB jest prawdziwe, α1 też jest prawdziwe.
Stąd KB |= α1: nie ma dołu w [1,2]. Możemy też to zobaczyć w niektórych modelach, w których KB jest prawdziwe, α2 jest fałszywe.
Stąd KB nie pociąga za sobą α2: agent nie może stwierdzić, że w [2,2] nie ma dołu. (Nie może też stwierdzić, że w [2,2] jest dół).
Powyższy przykład nie tylko ilustruje wynikanie, ale także pokazuje, w jaki sposób definicja wynikania może być zastosowana do wyprowadzania wniosków – to znaczy do wnioskowania logicznego. Algorytm wnioskowania przedstawiony na rysunku 7.5 nazywa się sprawdzaniem modelu, ponieważ wylicza wszystkie możliwe modele do sprawdzenia, czy jest prawdziwe we wszystkich modelach, w których KB jest prawdziwe, to znaczy, że M(KB) ⊆ M(α)
W zrozumieniu wnioskowania i wnioskowania pomocne może być myślenie o zbiorze wszystkich konsekwencji KB jako stogu siana i jako igle. Entailment jest jak igła w stogu siana; wnioskowanie jest jak znalezienie go. To rozróżnienie jest zawarte w pewnym formalnym zapisie: jeśli algorytm wnioskowania może pochodzić z KB , zapiszemy
![]()
co jest wymawiane jako „ α pochodzi od KB przez i ” lub „ i pochodzi od α od KB”. Algorytm wnioskowania, który wyprowadza tylko zaciągnięte zdania, nazywa się zachowaniem dźwięku lub prawdy. Zdrowość jest wysoce pożądaną właściwością. Niewłaściwa procedura wnioskowania zasadniczo wymyśla rzeczy w miarę postępu — zapowiada odkrycie nieistniejących igieł. Łatwo zauważyć, że sprawdzanie modelu, jeśli ma zastosowanie, jest rozsądną procedurą.
Pożądana jest również właściwość zupełności: algorytm wnioskowania jest kompletny, jeśli może wyprowadzić dowolne zdanie, które jest z nim związane. W przypadku prawdziwych stogów siana, których rozmiar jest skończony, wydaje się oczywiste, że systematyczne badanie zawsze może zdecydować, czy igła znajduje się w stogu siana. Jednak dla wielu baz wiedzy stóg konsekwencji jest nieskończony, a kompletność staje się ważną kwestią. Na szczęście istnieją kompletne procedury wnioskowania dla logik, które są wystarczająco ekspresyjne, aby obsłużyć wiele baz wiedzy. Opisaliśmy proces rozumowania, którego wnioski gwarantują prawdziwość w każdym świecie, w którym przesłanki są prawdziwe; w szczególności, jeśli KB jest prawdziwe w świecie rzeczywistym, to każde zdanie wyprowadzone z KB za pomocą procedury wnioskowania dźwiękowego jest również prawdziwe w świecie rzeczywistym. Tak więc, podczas gdy proces wnioskowania działa na „składni” – wewnętrznych konfiguracjach fizycznych, takich jak bity w rejestrach lub wzory elektrycznych impulsów w mózgu – proces ten odpowiada relacji w świecie rzeczywistym, w której pewien aspekt świata rzeczywistego ma miejsce z racji inne aspekty realnego świata. Tę zależność między światem a reprezentacją ilustruje rysunek
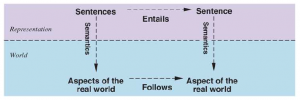
Ostatnią kwestią do rozważenia jest uziemienie – związek między logicznymi procesami rozumowania a rzeczywistym środowiskiem, w którym istnieje agent. W szczególności, skąd wiemy, że KB jest prawdziwe w prawdziwym świecie? (W końcu KB to po prostu „składnia” w głowie agenta.) Jest to pytanie filozoficzne, o którym napisano wiele, wiele książek. Prostą odpowiedzią jest to, że czujniki agenta tworzą połączenie. Na przykład nasz agent ze świata wumpusa ma czujnik zapachu. Program agenta tworzy odpowiednie zdanie za każdym razem, gdy pojawia się zapach. Wtedy, ilekroć to zdanie znajduje się w bazie wiedzy, jest prawdziwe w prawdziwym świecie. Tak więc znaczenie i prawdziwość zdań percepcyjnych są definiowane przez procesy odczuwania i konstruowania zdań, które je wytwarzają. A co z resztą wiedzy agenta, na przykład z przekonaniem, że wumpusy powodują zapachy na sąsiednich placach? Nie jest to bezpośrednia reprezentacja pojedynczego spostrzeżenia, ale ogólna zasada – wywodząca się być może z doświadczenia percepcyjnego, ale nie tożsama ze stwierdzeniem tego doświadczenia. Takie ogólne zasady są tworzone przez proces konstruowania zdań zwany uczeniem. Uczenie się jest omylne. Może się zdarzyć, że wumpusy powodują nieprzyjemne zapachy, z wyjątkiem 29 lutego w latach przestępnych, kiedy to biorą kąpiel. Dlatego KB , może nie być prawdziwe w prawdziwym świecie, ale przy dobrych procedurach uczenia się jest powód do optymizmu.