Miesiąc: listopad 2021

Przejdźmy teraz do składni logiki pierwszego rzędu. Niecierpliwy czytelnik może uzyskać pełny opis z gramatyki formalnej na rysunku

Podstawowymi elementami składniowymi logiki pierwszego rzędu są symbole reprezentujące obiekty, relacje i funkcje. Symbole występują zatem w trzech rodzajach: symbole stałe, które oznaczają przedmioty; symbole predykatów, które oznaczają relacje; i symbole funkcyjne, które oznaczają funkcje. Przyjmujemy konwencję, że te symbole zaczynają się od wielkich liter. Na przykład możemy użyć stałych symboli Richard i John; symbole predykatu Brother, OnHead, Person, King i Crown; oraz symbol funkcji LewaNoga. Podobnie jak w przypadku symboli propozycji, wybór nazw zależy wyłącznie od użytkownika. Każdy predykat i symbol funkcji ma arity, która ustala liczbę argumentów. Każdy model musi dostarczyć informacji wymaganych do ustalenia, czy dane zdanie jest prawdziwe czy fałszywe. Tak więc, oprócz swoich obiektów, relacji i funkcji, każdy model zawiera interpretację, która dokładnie określa, do których obiektów, relacji i funkcji odnoszą się symbole stałej, predykatu i funkcji. Jedna z możliwych interpretacji dla naszego przykładu – którą logik nazwałby interpretacją zamierzoną – jest następująca:

* Ryszard odnosi się do Ryszarda Lwie Serce, a Jan do złego króla Jana.

* Brat odnosi się do relacji braterskiej – czyli zbioru krotek obiektów; OnHead to relacja, która utrzymuje się między koroną a królem Janem; Osoba, Król i Korona to relacje jednoargumentowe, które identyfikują osoby, królów i korony.

* LeftLeg odnosi się do funkcji „lewej nogi” zdefiniowanej w równaniu.

Oczywiście istnieje wiele innych możliwych interpretacji. Na przykład jedna z interpretacji odwzorowuje Ryszarda na koronę, a Jana na lewą nogę króla Jana. W modelu jest pięć obiektów, więc istnieje 25 możliwych interpretacji tylko dla stałych symboli Richard i John. Zauważ, że nie wszystkie obiekty muszą mieć nazwę – na przykład zamierzona interpretacja nie nazywa korony ani nóg. Możliwe jest również, że obiekt ma kilka nazw; istnieje interpretacja, w której zarówno Ryszard, jak i Jan odnoszą się do korony. Jeśli uważasz, że ta możliwość jest myląca, pamiętaj, że w logice zdań całkiem możliwe jest posiadanie modelu, w którym zarówno Cloudy, jak i Sunny są prawdziwe; zadaniem bazy wiedzy jest wykluczenie modeli, które są niezgodne z naszą wiedzą. Podsumowując, model w logice pierwszego rzędu składa się ze zbioru obiektów i interpretacji, która odwzorowuje stałe symbole na obiekty, symbole funkcyjne na funkcje na tych obiektach i symbole predykatów na relacje. Podobnie jak w przypadku logiki zdań, implikacja, słuszność itd. są definiowane w kategoriach wszystkich możliwych modeli. Aby zorientować się, jak wygląda zestaw wszystkich możliwych modeli, zobacz Rysunek. Pokazuje, że modele różnią się liczbą obiektów, które zawierają – od jednego do nieskończoności – oraz sposobem, w jaki symbole stałe mapują się na obiekty.

Ponieważ liczba modeli pierwszego rzędu jest nieograniczona, nie możemy sprawdzić implikacji przez wyliczenie ich wszystkich (tak jak zrobiliśmy to w przypadku logiki zdań). Nawet jeśli liczba obiektów jest ograniczona, liczba kombinacji może być bardzo duża. W przykładzie na rysunku 8.4 istnieje 137 506 194 466 modeli z sześcioma lub mniej obiektami.

Wcześniej mówiliśmy, że modele języka logicznego są strukturami formalnymi, które konstytuują rozważane światy możliwe. Każdy model łączy słownik zdań logicznych z elementami świata możliwego, dzięki czemu można ustalić prawdziwość dowolnego zdania. W ten sposób modele logiki zdań łączą symbole zdań z predefiniowanymi wartościami prawdy. Modele logiki pierwszego rzędu są znacznie ciekawsze. Po pierwsze, mają w sobie przedmioty! Dziedziną modelu jest zbiór obiektów lub elementów domeny, które zawiera. Domena musi być niepusta – każdy możliwy świat musi zawierać przynajmniej jeden obiekt. Matematycznie rzecz biorąc, nie ma znaczenia, jakie są te obiekty – liczy się tylko to, ile jest ich w każdym konkretnym modelu – ale dla celów pedagogicznych użyjemy konkretnego przykładu. Rysunek przedstawia model z pięcioma obiektami: Ryszard Lwie Serce, król Anglii od 1189 do 1199; jego młodszy brat, zły król Jan, który rządził od 1199 do 1215 roku; lewe nogi Richarda i Johna; i koronę.

Obiekty w modelu mogą być powiązane na różne sposoby. Na rysunku Richard i John są braćmi. Formalnie rzecz biorąc, relacja to po prostu zbiór krotek obiektów, które są ze sobą powiązane. (Krótka jest zbiorem obiektów ułożonych w ustalonym porządku i jest zapisana w nawiasach ostrych otaczających obiekty.) Zatem relacja braterstwa w tym modelu jest zbiorem

{⟨Richard the Lionheart, King John⟩, ⟨King John, Richard the Lionheart⟩}

(Tu nazwaliśmy obiekty w języku angielskim, ale jeśli chcesz, możesz w myślach zastąpić je obrazkami.) Korona znajduje się na głowie króla Jana, więc relacja „na głowie” zawiera tylko jedną krotkę, 〈korona , króla Jana. Relacje „brat” i „na głowie” są relacjami binarnymi – to znaczy łączą pary obiektów. Model zawiera również jednoargumentowe relacje lub właściwości: właściwość „osoby” jest prawdziwa zarówno w przypadku Richarda, jak i Johna; własność „króla” dotyczy tylko Jana (przypuszczalnie dlatego, że Ryszard nie żyje w tym momencie); a właściwość „korony” dotyczy tylko korony. Pewne rodzaje relacji najlepiej traktować jako funkcje, ponieważ dany obiekt musi być w ten sposób powiązany z dokładnie jednym obiektem. Na przykład każda osoba ma jedną lewą nogę, więc model ma jednoargumentową funkcję „lewa noga” – mapowanie z jednoelementowej krotki na obiekt – która obejmuje następujące mapowania:

Ściśle mówiąc, modele w logice pierwszego rzędu wymagają funkcji całkowitych, to znaczy, że każda krotka wejściowa musi mieć wartość. Zatem korona musi mieć lewą nogę, podobnie jak każda z lewych nóg. Istnieje techniczne rozwiązanie tego niezręcznego problemu, polegające na dodatkowym „niewidzialnym” obiekcie, jakim jest lewa noga wszystkiego, co nie ma lewej nogi, łącznie z nim samym. Na szczęście tak długo, jak nie czyni się twierdzeń o lewych nogach rzeczy, które nie mają lewych nóg, te szczegóły techniczne nie mają znaczenia. Do tej pory opisaliśmy elementy, które wypełniają modele dla logiki pierwszego rzędu. Inną istotną częścią modelu jest powiązanie tych elementów ze słownictwem zdań logicznych, które wyjaśnimy dalej.

Rozpoczniemy tę część od dokładniejszego określenia, w jaki sposób możliwe światy logiki pierwszego rzędu odzwierciedlają ontologiczne zaangażowanie w przedmioty i relacje. Następnie wprowadzamy różne elementy języka, wyjaśniając ich semantykę w miarę postępów. Główne kwestie dotyczą tego, w jaki sposób język ułatwia zwięzłe reprezentacje i jak jego semantyka prowadzi do solidnych procedur rozumowania.

Możemy przyjąć fundament logiki zdaniowej – deklaratywnej, kompozycyjnej semantyki niezależnej od kontekstu i jednoznacznej – i zbudować na tym fundamencie bardziej ekspresyjną logikę, zapożyczając idee reprezentacyjne z języka naturalnego, unikając jego wad. Kiedy patrzymy na składnię języka naturalnego, najbardziej oczywistymi elementami są rzeczowniki i wyrażenia rzeczownikowe, które odnoszą się do przedmiotów (kwadraty, doły, wumpuses) oraz czasowniki i frazy czasownikowe wraz z przymiotnikami i przysłówkami, które odnoszą się do relacji między przedmiotami (jest przewiewny, sąsiaduje z pędami). Niektóre z tych relacji są funkcjami – relacjami, w których istnieje tylko jedna „wartość” dla danego „dane wejściowego”. Łatwo jest zacząć wymieniać przykłady obiektów, relacji i funkcji:

* Przedmioty: ludzie, domy, liczby, teorie, Ronald McDonald, kolory, gry w baseball, wojny, wieki…

* Relacje: mogą to być relacje jednoargumentowe lub właściwości, takie jak czerwony, okrągły, fałszywy, pierwszy, wielopiętrowy … lub bardziej ogólne relacje -arne, takie jak brat, większy niż, wewnątrz, część, ma kolor, wystąpił po, posiada, wchodzi pomiędzy, …

* Funkcje: ojciec, najlepszy przyjaciel, trzecia runda, jeszcze jedna, początek …

Rzeczywiście, prawie każde stwierdzenie może być traktowane jako odnoszące się do przedmiotów i właściwości lub relacji. Oto kilka przykładów:

* „Jeden plus dwa równa się trzy”. Przedmioty: jeden, dwa, trzy, jeden plus dwa; Relacja: równa się; Funkcja: plus. („Jeden plus dwa” to nazwa obiektu otrzymywana przez zastosowanie funkcji „plus” do obiektów „jeden” i „dwa”. „Trzy” to inna nazwa tego obiektu.)

* „Kwadraty sąsiadujące z wumpusem śmierdzą”. Obiekty: wumpusy, kwadraty; Właściwość: śmierdząca; Relacja: sąsiedztwo.

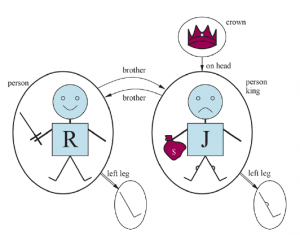
* „Zły król Jan rządził Anglią w 1200 roku”. Obiekty: Jan, Anglia, 1200; Relacja: rządził podczas; Właściwości: zło, król.

Język logiki pierwszego rzędu, którego składnię i semantykę zdefiniujemy w następnym podrozdziale, zbudowany jest wokół obiektów i relacji. Było to ważne dla matematyki, filozofii i sztucznej inteligencji właśnie dlatego, że te dziedziny – a nawet większość codziennej ludzkiej egzystencji – można pożytecznie traktować jako zajmujące się przedmiotami i relacjami między nimi. Logika pierwszego rzędu może również wyrażać fakty dotyczące niektórych lub wszystkich obiektów we wszechświecie. Umożliwia to reprezentowanie ogólnych praw lub zasad, takich jak stwierdzenie „Kwadraty sąsiadujące z wumpusem są śmierdzące”. Podstawowa różnica między logiką zdaniową a logiką pierwszego rzędu leży w ontologicznym zobowiązaniu każdego języka — to znaczy w tym, co on zakłada na temat natury rzeczywistości. Matematycznie to zobowiązanie wyraża się w naturze modeli formalnych, w odniesieniu do których określa się prawdziwość zdań. Na przykład logika zdań zakłada, że ​​istnieją fakty, które albo obowiązują w świecie, albo nie. Każdy fakt może być w jednym z dwóch stanów – prawda lub fałsz – i każdy model przypisuje prawdę lub fałsz każdemu symbolowi zdania . Logika pierwszego rzędu zakłada więcej; mianowicie, że świat składa się z przedmiotów, które mają między sobą pewne relacje, które utrzymują się lub nie.  Modele formalne są odpowiednio bardziej skomplikowane niż te dla logiki zdań. To ontologiczne zobowiązanie jest wielką siłą logiki (zarówno propozycjonalnej, jak i pierwszego rzędu), ponieważ pozwala nam zacząć od prawdziwych stwierdzeń i wywnioskować inne prawdziwe. Jest szczególnie skuteczny w dziedzinach, w których każde twierdzenie ma wyraźne granice, takich jak matematyka lub świat wumpusów, gdzie kwadrat albo ma wgłębienie, albo nie; nie ma możliwości kwadratu z niejasnym wcięciem przypominającym wgłębienie. Ale w prawdziwym świecie wiele propozycji ma niejasne granice: Czy Wiedeń jest dużym miastem? Czy ta restauracja służy pysznym jedzeniem? Czy ta osoba jest wysoka? To zależy, kogo zapytasz, a ich odpowiedź może być „w pewnym sensie”. Jedną z odpowiedzi jest udoskonalenie reprezentacji: jeśli prymitywna linia dzieląca miasta na „duże” i „niewielkie” pozostawia zbyt wiele informacji dla danej aplikacji, można zwiększyć liczbę kategorii rozmiaru lub użyć symbolu funkcji populacji. Inne proponowane rozwiązanie pochodzi z logiki rozmytej, która zakłada ontologiczne zobowiązanie, że zdania mają stopień prawdziwości od 0 do 1. Na przykład zdanie „Wiedeń to duże miasto” może być prawdziwe w stopniu 0,8 w logice rozmytej, podczas gdy „Paryż to duże miasto” może mieć wartość 0,9. Odpowiada to lepiej naszej intuicyjnej koncepcji świata, ale utrudnia wnioskowanie: zamiast jednej reguły do ​​ustalenia prawdziwości A Λ B , logika rozmyta potrzebuje różnych reguł w zależności od dziedziny. Inną możliwością, opisaną , jest przypisanie każdej koncepcji do punktu w przestrzeni wielowymiarowej, a następnie zmierzenie odległości między pojęciem „duże miasto” a pojęciem „Wiedeń” lub „Paryż”. Różne logiki specjalnego przeznaczenia czynią jeszcze dalsze zobowiązania ontologiczne; na przykład logika temporalna zakłada, że fakty zachodzą w określonych czasach i że te czasy (które mogą być punktami lub odstępami) są uporządkowane. Zatem logiki specjalnego przeznaczenia nadają pewnym rodzajom obiektów (i aksjomatów na ich temat) status „pierwszej klasy” w logice, zamiast po prostu definiować je w bazie wiedzy. Logika wyższego rzędu postrzega relacje i funkcje, do których odwołuje się logika pierwszego rzędu, jako same w sobie obiekty. Pozwala to na wysuwanie twierdzeń o wszystkich relacjach – na przykład można by chcieć zdefiniować, co to znaczy, że relacja jest przechodnia. W przeciwieństwie do większości logik specjalnego przeznaczenia, logika wyższego rzędu jest ściślej bardziej ekspresyjna niż logika pierwszego rzędu, w tym sensie, że niektóre zdania logiki wyższego rzędu nie mogą być wyrażone przez dowolną skończoną liczbę zdań logicznych pierwszego rzędu. Logikę można też scharakteryzować przez jej epistemologiczne zobowiązania – możliwe stany wiedzy, na które pozwala w odniesieniu do każdego faktu. Zarówno w logice zdaniowej, jak i pierwszego rzędu, zdanie reprezentuje fakt, a podmiot albo wierzy, że zdanie jest prawdziwe, wierzy, że jest fałszywe, albo nie ma opinii. Logiki te mają zatem trzy możliwe stany wiedzy o każdym zdaniu. Z drugiej strony systemy wykorzystujące teorię prawdopodobieństwa mogą mieć dowolny stopień przekonania lub subiektywnego prawdopodobieństwa, od 0 (całkowite niewiara) do 1 (całkowite przekonanie). Ważne jest, aby nie mylić stopnia wiary w teorię prawdopodobieństwa ze stopniem prawdziwości logiki rozmytej. Rzeczywiście, niektóre systemy rozmyte dopuszczają niepewność (stopień wiary) co do stopni prawdy. Na przykład, probabilistyczny agent świata wumpusa może sądzić, że wumpus jest w [1,3] z prawdopodobieństwem 0,75 i w [2, 3] z prawdopodobieństwem 0,25 (chociaż wumpus jest zdecydowanie w jednym konkretnym kwadracie).

Języki naturalne (takie jak angielski czy hiszpański) są rzeczywiście bardzo ekspresyjne. Udało nam się napisać prawie całą książkę w języku naturalnym, z rzadkimi tylko przeskokami do innych języków (głównie matematyki i diagramów). Językoznawstwo i filozofia języka mają długą tradycję, która postrzega język naturalny jako deklaratywny język reprezentacji wiedzy. Gdybyśmy mogli odkryć zasady języka naturalnego, moglibyśmy ich użyć w systemach reprezentacji i rozumowania i uzyskać korzyści z miliardów stron które zostały napisane w języku naturalnym. Współczesny pogląd na język naturalny polega na tym, że służy on jako środek komunikacji, a nie czysta reprezentacja. Kiedy mówca wskazuje i mówi: „Spójrz!” słuchacz dowiaduje się, że, powiedzmy, Superman wreszcie pojawił się nad dachami. Nie chcielibyśmy jednak powiedzieć, że zdanie „Spójrz!” reprezentuje ten fakt. Znaczenie zdania zależy raczej zarówno od samego zdania, jak i od kontekstu, w jakim zdanie zostało wypowiedziane. Najwyraźniej nie można było zapisać zdania takiego jak „Spójrz!” w bazie wiedzy i oczekiwać odzyskania jego znaczenia bez przechowywania reprezentacji kontekstu — co rodzi pytanie, w jaki sposób można przedstawić sam kontekst. Języki naturalne również cierpią z powodu niejednoznaczności, co jest problemem dla języka reprezentacji. Jak ujął to Pinker (1995): „Kiedy ludzie myślą o wiośnie, z pewnością nie są zdezorientowani, czy myślą o porze roku, czy o czymś, co się dzieje – a jeśli jedno słowo może odpowiadać dwóm myślom, myśli nie mogą być słowa.” Słynna hipoteza Sapira – Whorfa. Whorfa głosi, że na nasze rozumienie świata silny wpływ ma język, którym mówimy. Z pewnością prawdą jest, że różne wspólnoty językowe w różny sposób dzielą świat. Francuzi mają dwa słowa „chaise” i „fauteuil”, na określenie koncepcji, którą anglojęzyczni określają jednym: „krzesło”. Ale osoby mówiące po angielsku mogą łatwo rozpoznać kategorię fauteuil i nadać jej nazwę – z grubsza „fotel z otwartymi ramionami” – więc czy język naprawdę robi różnicę? Whorf opierał się głównie na intuicji i spekulacjach, a jego idee zostały w dużej mierze odrzucone, ale w międzyczasie mamy rzeczywiste dane z badań antropologicznych, psychologicznych i neurologicznych. Na przykład, czy pamiętasz, które z poniższych dwóch fraz stanowiło początek sekcji ?

„W tej sekcji omawiamy naturę języków reprezentacji . . ”.

„Ta sekcja obejmuje temat języków reprezentacji wiedzy . . ”.

Wanner przeprowadził podobny eksperyment i stwierdził, że badani dokonywali właściwego wyboru na poziomie losowym – w około 50% przypadków – ale pamiętali treść tego, co czytali z dokładnością lepszą niż 90%. Sugeruje to, że ludzie interpretują słowa, które czytają i tworzą wewnętrzną reprezentację niewerbalną, a dokładne słowa nie mają konsekwencji. Bardziej interesujący jest przypadek, w którym pojęcie jest całkowicie nieobecne w języku. Osoby posługujące się australijskim językiem aborygeńskim Guugu Yimithirr nie mają słów na określenie kierunków względnych (lub egocentrycznych), takich jak przód, tył, prawo lub lewo. Zamiast tego używają bezwzględnych wskazówek, mówiąc na przykład ekwiwalent „boli mnie północne ramię”. Ta różnica w języku ma wpływ na zachowanie: osoby mówiące w języku Guugu Yimithirr są lepsze w nawigacji w otwartym terenie, podczas gdy osoby mówiące po angielsku lepiej radzą sobie z umieszczaniem widełek po prawej stronie tablicy. Język wydaje się również wpływać na myślenie poprzez pozornie arbitralne cechy gramatyczne, takie jak rodzaj rzeczowników. Na przykład „most” to rodzaj męski w języku hiszpańskim i żeński w języku niemieckim. Boroditsky (2003) poprosił badanych o wybranie angielskich przymiotników opisujących zdjęcie konkretnego mostu. Hiszpanie wybrali duże, niebezpieczne, mocne i wysokie, podczas gdy niemieccy wybrali piękne, eleganckie, delikatne i smukłe.

Słowa mogą służyć jako punkty zaczepienia, które wpływają na to, jak postrzegamy świat. Loftus i Palmer pokazali badanym eksperymentalnym film o wypadku samochodowym. Osoby, którym zadano pytanie: „Jak szybko jechały samochody, gdy się ze sobą kontaktowały? ” zgłosiło średnią 32 mil na godzinę, podczas gdy osoby, którym zadano pytanie ze słowem „rozbity” zamiast „skontaktowano”, zgłosiły 41 mil na godzinę dla tych samych samochodów w tym samym filmie. Ogólnie rzecz biorąc, istnieją wymierne, ale niewielkie różnice w przetwarzaniu poznawczym przez osoby mówiące różnymi językami, ale nie ma przekonujących dowodów na to, że prowadzi to do poważnych różnic w światopoglądzie. W logicznym systemie rozumowania, który wykorzystuje spójną postać normalną (CNF), widzimy, że Formy językowe „¬(A ∨ B) ” i „¬A ∧ ¬B” są takie same, ponieważ możemy zajrzeć do wnętrza systemu i zobaczyć, że te dwa zdania są przechowywane jako ta sama kanoniczna forma CNF. Z ludzkim mózgiem można zrobić coś podobnego. Mitchell i inni umieścili badanych w funkcjonalnej maszynie do obrazowania metodą rezonansu magnetycznego (fMRI), pokazali im słowa takie jak „selery” i zobrazowali ich mózgi. Program uczenia maszynowego wyszkolony na parach (słowo, obraz) był w stanie poprawnie przewidzieć 77% czasu w przypadku zadań wyboru binarnego (np. „seler” lub „samolot”). System może nawet przewidywać na poziomie powyżej szansy słowa, których nigdy wcześniej nie widział na obrazie fMRI (poprzez uwzględnienie obrazów powiązanych słów) oraz ludzi, których nigdy wcześniej nie widział (dowodząc, że fMRI ujawnia pewien poziom wspólnej reprezentacji ludzi ). Tego typu prace są wciąż w powijakach, ale fMRI (i inne technologie obrazowania, takie jak elektrofizjologia wewnątrzczaszkowa (Sahin i in., 2009)) obiecują dostarczyć nam znacznie bardziej konkretnych pomysłów na to, jak wyglądają reprezentacje wiedzy ludzkiej. Z punktu widzenia logiki formalnej reprezentowanie tej samej wiedzy na dwa różne sposoby nie ma absolutnie żadnego znaczenia; te same fakty można wyprowadzić z obu reprezentacji. W praktyce jednak jedno przedstawienie może wymagać mniejszej liczby kroków, aby wyciągnąć wniosek, co oznacza, że ​​osoba prowadząca rozumowanie mająca ograniczone zasoby może dojść do wniosku przy użyciu jednej reprezentacji, ale nie drugiej. W przypadku zadań niededukcyjnych, takich jak uczenie się na podstawie doświadczenia, wyniki są z konieczności zależne od formy użytych reprezentacji. Później pokażemy, że kiedy program nauczania bierze pod uwagę dwie możliwe teorie świata, z których obie są zgodne ze wszystkimi danymi, najczęstszym sposobem na zerwanie więzi jest wybranie najbardziej zwięzłej teorii — a to zależy od języka używane do reprezentowania teorii. Tak więc wpływ języka na myślenie jest nieunikniony dla każdego podmiotu, który się uczy.

W tej sekcji omówimy naturę języków reprezentacji. Języki programowania (takie jak C++, Java czy Python) to największa klasa powszechnie używanych języków formalnych. Struktury danych w programach mogą służyć do reprezentowania faktów; na przykład program może użyć tablicy 4 x 4 do reprezentowania zawartości świata wumpus. Tak więc instrukcja języka programowania World[2,2] ← Pit to dość naturalny sposób na stwierdzenie, że tam to zagłębienie w kwadracie [2,2]. Zestawienie ciągu takich stwierdzeń wystarczy do przeprowadzenia symulacji świata wumpusów. To, czego brakuje w językach programowania, to ogólny mechanizm wyprowadzania faktów z innych faktów; każda aktualizacja struktury danych jest wykonywana przez procedurę specyficzną dla domeny, której szczegóły są wyprowadzane przez programistę z jego własnej wiedzy o domenie. Takiemu podejściu proceduralnemu można przeciwstawić deklaratywną naturę logiki zdań, w której wiedza i wnioskowanie są oddzielone, a wnioskowanie jest całkowicie niezależne od dziedziny. Bazy danych SQL wykorzystują mieszankę wiedzy deklaratywnej i proceduralnej.

Drugą wadą struktur danych w programach (i bazach danych) jest brak łatwego sposobu powiedzenia, na przykład „W [2,2] lub [3,1] jest dziura” lub „Jeśli wumpus jest w [1,1] to nie ma go w [2,2].” Programy mogą przechowywać pojedynczą wartość dla każdej zmiennej, a niektóre systemy pozwalają, aby wartość była „nieznana”, ale brakuje im wyrazistości wymaganej do bezpośredniego przetwarzania częściowych informacji.

Logika zdań jest językiem deklaratywnym, ponieważ jej semantyka opiera się na relacji prawdziwości między zdaniami a możliwymi światami. Ma również wystarczającą siłę wyrazu, aby radzić sobie z częściowymi informacjami, używając alternatywy i negacji. Logika zdań ma trzecią właściwość pożądaną w językach reprezentacji, a mianowicie kompozycyjność. W języku kompozycyjnym znaczenie zdania jest funkcją znaczenia jego części. Na przykład znaczenie „S1,4 Λ S1,2 ” jest powiązane ze znaczeniami „S1,4” i „S1,2 ”. Byłoby bardzo dziwne, gdyby „S1,4 ” oznaczało, że w kwadracie jest smród [1,4] a „S1,2 ” oznacza, że ​​smród w kwadracie [1,2], ale „S1,4 Λ S1,2 ” oznaczało, że Francja i Polska zremisowały 1:1 w zeszłotygodniowym meczu eliminacyjnym hokeja na lodzie.

Jednak logice zdań, jako reprezentacji na czynniki, brakuje wyrazistej mocy, by zwięźle opisać środowisko z wieloma obiektami. Na przykład byliśmy zmuszeni napisać osobną zasadę dotyczącą bryz i dołów dla każdego kwadratu, na przykład

W języku angielskim wydaje się dość łatwe, aby raz na zawsze powiedzieć: „Kwadraty przylegające do dołów są przewiewne”. Składnia i semantyka języka angielskiego umożliwiają zwięzłe opisanie środowiska: język angielski, podobnie jak logika pierwszego rzędu, jest reprezentacją strukturalną.

Wprowadziliśmy agentów opartych na wiedzy i pokazaliśmy, jak zdefiniować logikę, dzięki której tacy agenci mogą wnioskować o świecie. Główne punkty są następujące:

* Inteligentni agenci potrzebują wiedzy o świecie, aby podejmować dobre decyzje.

* Wiedza jest zawarta w agentach w formie zdań w języku reprezentacji wiedzy, które są przechowywane w bazie wiedzy.

* Agent oparty na wiedzy składa się z bazy wiedzy i mechanizmu wnioskowania. Działa, przechowując zdania o świecie w swojej bazie wiedzy, używając mechanizmu wnioskowania do wywnioskowania nowych zdań i używając tych zdań, aby zdecydować, jakie działanie podjąć.

* Język reprezentacji jest zdefiniowany przez swoją składnię, która określa strukturę zdań i jego semantykę, która określa prawdziwość każdego zdania w każdym możliwym świecie lub modelu.

* Relacja wynikania między zdaniami jest kluczowa dla naszego rozumienia rozumowania. Zdanie α pociąga za sobą kolejne zdanie β, jeśli β jest prawdziwe we wszystkich światach, w których α jest prawdziwe. Równoważne definicje obejmują ważność zdania α => β oraz niespełnialność zdania α Λ ¬β.

* Wnioskowanie to proces wyprowadzania nowych zdań ze starych. Algorytmy wnioskowania dźwiękowego wyprowadzają tylko zdania, które są implikowane; kompletne algorytmy wyprowadzają wszystkie zdania, które są z nimi związane.

* Logika zdań to prosty język składający się z symboli zdań i spójników logicznych. Może obsługiwać twierdzenia, o których wiadomo, że są prawdziwe, fałszywe lub zupełnie nieznane.

* Zbiór możliwych modeli, przy ustalonym słowniku zdań, jest skończony, więc wyciągnięcie można sprawdzić, wyliczając modele. Wydajne algorytmy wnioskowania sprawdzające model dla logiki zdań obejmują metody śledzenia wstecznego i wyszukiwania lokalnego i często mogą szybko rozwiązywać duże problemy.

* Reguły wnioskowania to wzorce wnioskowania dźwiękowego, które można wykorzystać do znalezienia dowodów. Reguła rozstrzygania daje kompletny algorytm wnioskowania dla baz wiedzy, które są wyrażone w spójnych postaciach normalnych. Łańcuchy do przodu i łańcuchy wsteczne są bardzo naturalnymi algorytmami rozumowania dla baz wiedzy w formie Horn.

* Do znalezienia rozwiązań można użyć lokalnych metod wyszukiwania, takich jak WALKSAT. Takie algorytmy są dobre, ale niekompletne.

* Estymacja stanów logicznych polega na utrzymywaniu logicznego zdania opisującego zbiór możliwych stanów zgodnych z historią obserwacji. Każdy krok aktualizacji wymaga wnioskowania przy użyciu przejściowego modelu środowiska, który jest zbudowany z aksjomatów stanów następczych, które określają, w jaki sposób zmienia się każdy płynny.

* Decyzje w ramach agenta logicznego mogą być podejmowane przez rozwiązywanie SAT: znalezienie możliwych modeli określających przyszłe sekwencje działań, które osiągną cel. To podejście działa tylko w środowiskach w pełni obserwowalnych lub bezczujnikowych.

* Logika zdań nie skaluje się do środowisk o nieograniczonej wielkości, ponieważ brakuje jej siły wyrazu, by zwięźle radzić sobie z czasem, przestrzenią i uniwersalnymi wzorcami relacji między obiektami.

W tej sekcji pokazujemy, jak tworzyć plany za pomocą logicznego wnioskowania. Podstawowa idea jest bardzo prosta:

1. Skonstruuj zdanie, które zawiera
2. Init0 , kolekcja twierdzeń o stanie początkowym;
3. Transition¹ … Transition^t , aksjomaty stanu następcy dla wszystkich możliwych działań w każdym czasie do pewnego maksymalnego czasu t;
4. twierdzenie, że cel został osiągnięty w czasie t : HaeGoldt Λ ClimbeOutt
5. Przedstaw całe zdanie osobie rozwiązującej SAT. Jeśli solver znajdzie satysfakcjonujący model, cel jest osiągalny; jeśli zdanie jest niezadowalające, problem jest nie do rozwiązania.
6. Zakładając, że model został znaleziony, wyodrębnij z modelu te zmienne, które reprezentują działania i są przypisane true. Razem reprezentują plan osiągnięcia celów.

Procedura planowania propozycji, SATPLAN, jest pokazana na rysunku . Realizuje podstawową ideę właśnie podaną, z jednym zwrotem akcji. Ponieważ agent nie wie, ile kroków musi wykonać, aby osiągnąć cel, algorytm próbuje każdą możliwą liczbę kroków t, aż do pewnej maksymalnej możliwej długości planu T_max. W ten sposób gwarantuje się znalezienie najkrótszego planu, jeśli taki istnieje. Ze względu na sposób, w jaki SATPLAN szuka rozwiązania, to podejście nie może być stosowane w częściowo obserwowalnym środowisku; SATPLAN po prostu ustawi nieobserwowalne zmienne na wartości potrzebne do stworzenia rozwiązania.

Kluczowym krokiem w korzystaniu z SATPLAN jest budowa bazy wiedzy. Mogłoby się wydawać, po przypadkowym przyjrzeniu się, że aksjomaty świata wumpus w Sekcji 7.7.1 wystarczą dla kroków 1(a) i 1(b) powyżej. Istnieje jednak znacząca różnica między wymaganiami dotyczącymi pociągania (testowane przez ASK) a wymaganiami spełnialności. Rozważmy na przykład lokalizację agenta, początkowo [1,1] i załóżmy, że mało ambitnym celem agenta jest bycie w [2,1] w czasie 1. Początkowa baza wiedzy zawiera L⁰_1,1, a celem jest L¹_2,1 . Używając ASK, możemy udowodnić L¹_2,1, czy Forward⁰ jest potwierdzony, i, co uspokaja, nie możemy udowodnić L^1,_2,1, jeśli, powiedzmy, Shoot⁰ jest potwierdzony zamiast tego. Teraz SATPLAN znajdzie plan [Forward⁰]; jak na razie dobrze. Niestety SATPLAN również znajduje plan [Shoot⁰]. Jak to możliwe? Aby się tego dowiedzieć, sprawdzamy model, który konstruuje SATPLAN: zawiera on przypisanie L⁰_2,1 , czyli agent może być w [2,1] w czasie 1, będąc tam w czasie 0 i strzelając. Ktoś mógłby zapytać: „Czy nie mówiliśmy, że agent jest w [1,1] w czasie 0?” Tak, zrobiliśmy, ale nie powiedzieliśmy agentowi, że nie może być w dwócha miejsca na raz! Bo implikacja L⁰_2,1jest nieznana i dlatego nie może być użyta w dowodzie; z drugiej strony spełnialność L⁰_2,1 jest nieznana i dlatego może być ustawiona na dowolną wartość, która pomaga w urzeczywistnieniu celu. SATPLAN jest dobrym narzędziem do debugowania baz wiedzy, ponieważ ujawnia miejsca, w których brakuje wiedzy. W tym konkretnym przypadku możemy naprawić bazę wiedzy, stwierdzając, że na każdym kroku czasu agent znajduje się dokładnie w jednym miejscu, używając zbioru zdań podobnych do tych, które są używane do stwierdzenia istnienia dokładnie jednego wumpusa. Alternatywnie możemy potwierdzić ¬L⁰_2,1dla wszystkich lokalizacji innych niż [1,1]; aksjomat stanu następcy dla lokalizacji zajmuje się kolejnymi krokami czasowymi. Te same poprawki działają również w celu upewnienia się, że agent ma jedną i tylko jedną orientację na raz. SATPLAN ma jednak w zanadrzu więcej niespodzianek. Po pierwsze, znajduje modele z niemożliwymi akcjami, takimi jak strzelanie bez strzały. Aby zrozumieć dlaczego, musimy dokładniej przyjrzeć się temu, co aksjomaty stanów następczych (takie jak Równanie (7.3) ) mówią o działaniach, których warunki wstępne nie są spełnione. Aksjomaty właściwie przewidują, że nic się nie stanie, gdy taka akcja zostanie wykonana, ale nie mówią, że akcja nie może być wykonana! Aby uniknąć generowania planów z niedozwolonymi akcjami, musimy dodać aksjomaty warunków wstępnych Aksjomaty warunków wstępnych stwierdzające, że wystąpienie akcji wymaga spełnienia warunków wstępnych. , że

Gwarantuje to, że jeśli plan w dowolnym momencie wybierze akcję Strzelaj, agent musi mieć w tym czasie strzałkę. Drugą niespodzianką SATPLAN jest tworzenie planów z wieloma jednoczesnymi działaniami. Na przykład może wymyślić model, w którym oba Forward⁰ i  Shoot⁰ są prawdziwe, co jest niedozwolone. Aby wyeliminować ten problem, wprowadzamy aksjomaty wykluczenia akcji: dla każdej pary akcji A^t_i i A^t_j dodajemy aksjomat

Można zauważyć, że chodzenie do przodu i strzelanie w tym samym czasie nie jest takie trudne, podczas gdy, powiedzmy, jednoczesne strzelanie i chwytanie jest raczej niepraktyczne. Nakładając aksjomaty wykluczenia działań tylko na pary działań, które naprawdę wzajemnie ze sobą kolidują, możemy zezwolić na plany obejmujące wiele jednoczesnych działań – a ponieważ SATPLAN znajduje najkrótszy plan prawny, możemy być pewni, że skorzysta z tej możliwości . Podsumowując, SATPLAN znajduje modele dla zdania zawierającego stan początkowy, cel, aksjomaty stanu następcy, aksjomaty warunków wstępnych i aksjomaty wykluczenia działania. Można wykazać, że ten zbiór aksjomatów jest wystarczający w tym sensie, że nie ma już żadnych fałszywych „rozwiązań”. Każdy model spełniający zdanie zdaniowe będzie poprawnym planem dla pierwotnego problemu. Nowoczesna technologia rozwiązywania SAT sprawia, że ​​podejście jest całkiem praktyczne. Na przykład solver w stylu DPLL nie ma trudności z wygenerowaniem rozwiązania dla instancji wumpus world.

W tej sekcji opisano deklaratywne podejście do konstrukcji agenta: agent działa poprzez połączenie asercji zdań w bazie wiedzy i wnioskowania logicznego. To podejście ma pewne słabości ukryte w wyrażeniach, takich jak „za każdy czas” i „dla każdego kwadratu [x,y] ”. Dla każdego praktycznego agenta te frazy muszą być zaimplementowane przez kod, który automatycznie generuje instancje ogólnego schematu zdań w celu wstawienia do bazy wiedzy. W wumpusowym świecie o rozsądnych rozmiarach — porównywalnym z niewielką grą komputerową — możemy potrzebować planszy 100 x 100 i 1000 kroków czasowych, prowadzących do baz wiedzy z dziesiątkami lub setkami milionów zdań. Nie tylko staje się to raczej niepraktyczne, ale także ilustruje głębszy problem: wiemy coś o świecie wumpusów – mianowicie, że „fizyka” działa w ten sam sposób we wszystkich kwadratach i krokach czasowych – czego nie możemy wyrazić bezpośrednio w język logiki zdań. Aby rozwiązać ten problem, potrzebujemy bardziej wyrazistego języka, w którym wyrażenia typu „za każdy czas” i „za każdy kwadrat [x,y]” można zapisać w naturalny sposób. Takim językiem jest logika pierwszego rzędu, opisana w rozdziale 8; W logice pierwszego rzędu świat Wumpusa o dowolnej wielkości i czasie trwania można opisać za pomocą około dziesięciu zdań logicznych, a nie dziesięciu milionów czy dziesięciu bilionów.

Program agenta działa całkiem dobrze, ale ma jedną główną słabość: w miarę upływu czasu koszty obliczeniowe związane z wywołaniami ASK rosną i rosną. Dzieje się tak głównie dlatego, że wymagane wnioskowania muszą cofać się coraz dalej w czasie i obejmować coraz więcej symboli zdaniowych. Oczywiście jest to nie do utrzymania – nie możemy mieć agenta, którego czas przetwarzania każdego spostrzeżenia rośnie proporcjonalnie do długości jego życia! To, czego naprawdę potrzebujemy, to stały czas aktualizacji – to znaczy niezależny od t . Oczywistą odpowiedzią jest zapisanie lub buforowanie wyników wnioskowania, aby proces wnioskowania w następnym kroku mógł opierać się, historię perceptów i wszystkie ich rozgałęzienia można zastąpić stanem przekonań – to jest pewną reprezentacją zbioru wszystkich możliwych aktualnych stanów świata. Proces aktualizowania stanu przekonań w miarę pojawiania się nowych percepcji nazywa się estymacją stanu. Podczas gdy stan przekonań był wyraźną listą stanów, tutaj możemy użyć zdania logicznego zawierającego symbole zdań związane z bieżącym krokiem czasowym, a także symbole atemporalne. Na przykład zdanie logiczne

reprezentuje zbiór wszystkich stanów w czasie 1, w którym wumpus żyje, agent znajduje się w [2,1], ten kwadrat jest przewiewny, a w [3,1] lub [2,2] jest dziura , lub obu. Utrzymanie dokładnego stanu przekonań jako logicznej formuły okazuje się nie być łatwe. Jeśli istnieją symbole płynne dla czasu t, to możliwe są 2ⁿ stany – to znaczy przyporządkowanie tym symbolom wartości logicznych. Otóż ​​zbiór stanów przekonań jest zbiorem mocy (zbiorem wszystkich podzbiorów) zbioru stanów fizycznych. Istnieją 2ⁿ stany fizyczne, stąd  2ⁿ stany wiary. Nawet gdybyśmy użyli możliwie najbardziej zwartego kodowania formuł logicznych, z każdym stanem przekonań reprezentowanym przez unikalną liczbę binarną, potrzebowalibyśmy liczb z log₂(2²ⁿ) = 2ⁿ bitami do oznaczenia aktualnego stanu przekonań. Oznacza to, że dokładne oszacowanie stanu może wymagać formuł logicznych, których rozmiar jest wykładniczy w liczbie symboli. Jednym z bardzo powszechnych i naturalnych schematów przybliżonego szacowania stanu jest reprezentowanie stanów przekonań jako koniunkcji literałów, czyli formuł 1-CNF. Aby to zrobić, program agenta po prostu próbuje udowodnić X^t i ¬X^t dla każdego symbolu X^t (jak również dla każdego symbolu atemporalnego, którego wartość prawdy nie jest jeszcze znana), biorąc pod uwagę stan wiary w t-1 . Połączenie możliwych do udowodnienia literałów staje się nowym stanem przekonań, a poprzedni stan przekonań zostaje odrzucony. Ważne jest, aby zrozumieć, że ten schemat może z czasem utracić pewne informacje. Na przykład, gdyby zdanie w równaniu było prawdziwym stanem przekonań, to ani P_3,1 ani P_2,2 nie byłyby indywidualnie udowodnione i żadne z nich nie pojawiłoby się w stanie przekonania 1-CNF. Z drugiej strony, ponieważ każdy literał w stanie przekonań 1-CNF jest udowodniony na podstawie poprzedniego stanu przekonań, a początkowy stan przekonań jest prawdziwym twierdzeniem, wiemy, że cały stan wiary 1-CNF musi być prawdziwy. Zatem zbiór możliwych stanów reprezentowanych przez stan przekonania 1-CNF obejmuje wszystkie stany, które są faktycznie możliwe przy pełnej historii percepcji. Jak pokazano na rysunku 7.21, stan przekonania 1-CNF działa jako prosta zewnętrzna otoczka lub konserwatywne przybliżenie wokół dokładnego stanu przekonania. Uważamy, że idea konserwatywnych przybliżeń do skomplikowanych zestawów jest powracającym motywem w wielu obszarach sztucznej inteligencji.

Zdolność do wywnioskowania różnych aspektów stanu świata można dość prosto połączyć z regułami warunku-działania , aby stworzyć agenta hybrydowego dla świata wumpusa. Rysunek pokazuje jeden z możliwych sposobów na zrobienie tego. Program agenta utrzymuje i aktualizuje bazę wiedzy oraz aktualny plan. Wstępna baza wiedzy zawiera aksjomaty atemporalne — te, które nie zależą od , takie jak aksjomat odnoszący przewiewność kwadratów do obecności dołów. W każdym kroku czasowym dodawane jest nowe zdanie percepcyjne wraz ze wszystkimi aksjomatami, które zależą od , takimi jak aksjomaty stanów następczych. (Następna sekcja wyjaśnia, dlaczego agent nie potrzebuje aksjomatów dla przyszłych kroków czasowych.) Następnie agent używa logicznego wnioskowania, zadając pytania z bazy wiedzy, aby ustalić, które kwadraty są bezpieczne, a które jeszcze nie zostały odwiedzone.

Główna część programu agenta konstruuje plan w oparciu o malejący priorytet celów. Po pierwsze, jeśli pojawi się blask, program konstruuje plan zdobycia złota, podążania drogą powrotną do początkowej lokalizacji i wyjścia z jaskini. W przeciwnym razie, jeśli nie ma aktualnego planu, program planuje trasę do najbliższego bezpiecznego placu, którego jeszcze nie odwiedził, upewniając się, że trasa przebiega tylko przez bezpieczne place. Planowanie trasy odbywa się za pomocą wyszukiwania A*, a nie za pomocą ASK. Jeśli nie ma bezpiecznych pól do zbadania, następnym krokiem – jeśli agent nadal ma strzałę – jest próba utworzenia bezpiecznego pola, strzelając w jedną z możliwych lokalizacji wumpusa. Określa się je, pytając gdzie w ASK(KB, ¬W_x,y) jest fałsz – to znaczy, gdzie nie wiadomo, czy nie ma wumpusa. Funkcja PLAN-SHOT (nie pokazana) wykorzystuje PLAN-ROUTE do zaplanowania sekwencji działań, które ułożą się w tym ujęciu. Jeśli to się nie powiedzie, program szuka kwadratu do zbadania, który nie jest niebezpieczny do udowodnienia — to znaczy kwadrat, dla którego ASK(KB, ¬OK^t_x,y)  zwraca wartość false. Jeśli nie ma takiego placu, misja jest niemożliwa i agent wycofuje się do [1,1] i wychodzi z jaskini.