Miesiąc: październik 2021

Ograniczenia preferencji często mogą być zakodowane jako koszty w poszczególnych przypisaniach zmiennych – na przykład przypisanie popołudniowego przedziału dla Prof. R kosztuje 2 punkty w stosunku do ogólnej funkcji celu, podczas gdy poranny przedział kosztuje 1. Dzięki temu sformułowaniu można rozwiązać CSP z preferencjami z optymalizacyjnymi metodami wyszukiwania, opartymi na ścieżce lub lokalnym. Taki problem nazywamy problemem ograniczonej optymalizacji lub COP. Programy liniowe to jedna klasa COP.

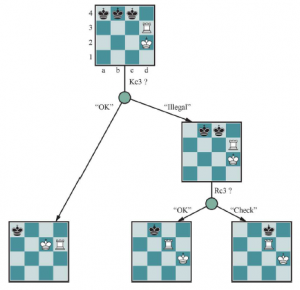
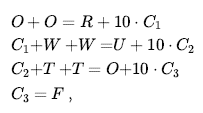Najprostszy rodzaj CSP obejmuje zmienne, które mają dyskretne, skończone domeny. Problemy z kolorowaniem map i planowanie z ograniczeniami czasowymi są tego rodzaju. Problem 8 hetmanów (rysunek 4.3 ) można również postrzegać jako CSP o skończonej dziedzinie, w którym zmienne Q1,…,Qs odpowiadają królowym w kolumnach od 1 do 8, a dziedzina każdej zmiennej określa możliwy wiersz liczby dla hetmana w tej kolumnie, D1={1,2,3,4,5,6,7,8} . Ograniczenia mówią, że żadne dwie hetmany nie mogą znajdować się w tym samym rzędzie lub po przekątnej. Dyskretna domena może być nieskończona, na przykład zbiór liczb całkowitych lub łańcuchów. (Gdybyśmy nie określili ostatecznego terminu problemu planowania zadań, byłaby nieskończona liczba czasów rozpoczęcia dla każdej zmiennej.) W przypadku nieskończonych dziedzin musimy użyć niejawnych ograniczeń, takich jak T1 + d1 ≤ T2, zamiast jawnych krotek wartości. Specjalne algorytmy rozwiązań (których nie omawiamy tutaj) istnieją dla więzów liniowych na zmiennych całkowitych — to znaczy takich, jak to właśnie podane, w którym każda zmienna występuje tylko w postaci liniowej. Można wykazać, że nie istnieje żaden algorytm rozwiązywania ogólnych nieliniowych ograniczeń na zmienne całkowite – problem jest nierozstrzygalny

Problemy z satysfakcją z ograniczeń z domenami ciągłymi są powszechne w świecie rzeczywistym i są szeroko badane w dziedzinie badań operacyjnych. Na przykład planowanie eksperymentów na Kosmicznym Teleskopie Hubble’a wymaga bardzo precyzyjnego czasu obserwacji; początek i koniec każdej obserwacji i manewru są zmiennymi o wartości ciągłej, które muszą być zgodne z różnymi ograniczeniami astronomicznymi, pierwszeństwa i mocy. Najbardziej znaną kategorią CSP w dziedzinie ciągłej jest problem programowania liniowego, gdzie ograniczenia muszą być liniowymi równościami lub nierównościami. Zadania programowania liniowego mogą być rozwiązywane wielomianem czasu w liczbie zmiennych. Badano również problemy z różnymi typami ograniczeń i funkcjami celu — programowanie kwadratowe, programowanie stożkowe drugiego rzędu i tak dalej. Problemy te stanowią ważny obszar matematyki stosowanej. Oprócz badania typów zmiennych, które mogą pojawiać się w CSP, warto przyjrzeć się typom ograniczeń. Najprostszym typem jest ograniczenie jednoargumentowe, które ogranicza wartość pojedynczej zmiennej. Na przykład w problemie kolorowania mapy może być tak, że mieszkańcy Australii Południowej nie będą tolerować koloru zielonego; możemy to wyrazić za pomocą jednoargumentowego ograniczenia . <(SA),SA  ≠ green.(Początkowa specyfikacja dziedziny zmiennej może być również postrzegana jako jednoargumentowe ograniczenie). Ograniczenie binarne dotyczy dwóch zmiennych. Na przykład  SA ≠ NSW jest ograniczeniem binarnym. Binarny CSP to taki, który ma tylko jednoargumentowe i binarne ograniczenia; może być reprezentowany jako graf ograniczeń. Możemy również zdefiniować ograniczenia wyższego rzędu. Na przykład ograniczenie trójskładnikowe Beetwen(X,Y,Z) można zdefiniować jako <(X,Y,Z), X < Y < Z lub X > Y > Z . Ograniczenie obejmujące dowolną liczbę zmiennych nazywa się ograniczeniem globalnym. (Nazwa jest tradycyjna, ale myląca, ponieważ globalne ograniczenie nie musi obejmować wszystkich zmiennych w problemie). Jednym z najczęstszych globalnych ograniczeń jest All di f f , które mówi, że wszystkie zmienne objęte ograniczeniem muszą mieć różne wartości. W zadaniach Sudoku wszystkie zmienne w rzędzie, kolumnie lub polu 3 x 3 muszą spełniać warunek All diff

Innym przykładem są łamigłówki kryptarytmetyczne (a). Każda litera w łamigłówce (a) byłoby to reprezentowane jako globalne ograniczenie All diff(F,T,U,W,R,O) . Ograniczenia dodawania na czterech kolumnach łamigłówki można zapisać jako następujące ograniczenia n-argumentowe:

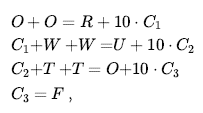
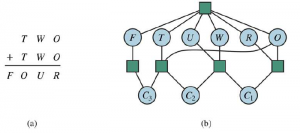
gdzie C₁,C₂ i C₃ są zmiennymi pomocniczymi reprezentującymi cyfrę przeniesioną do kolumny dziesiątek, setek lub tysięcy. Te ograniczenia można przedstawić na hipergrafie ograniczeń, takim jak ten pokazany na rysunku 6.2(b). Hipergraf składa się ze zwykłych węzłów (kół na rysunku) i hiperwęzłów (kwadratów), które reprezentują ograniczenia -arne — ograniczenia obejmujące n zmiennych.

Alternatywnie NARY prosi o udowodnienie, że każde ograniczenie domeny skończonej można zredukować do zestawu ograniczeń binarnych, jeśli wprowadzi się wystarczającą liczbę zmiennych pomocniczych. Oznacza to, że możemy przekształcić dowolny CSP w taki, który ma tylko ograniczenia binarne — co z pewnością upraszcza życie projektanta algorytmu. Innym sposobem konwersji -arnego CSP na binarny jest transformacja grafu dualnego: utwórz nowy graf, w którym będzie jedna zmienna dla każdego ograniczenia w oryginalnym grafie i jedno ograniczenie binarne dla każdej pary ograniczeń w oryginalnym grafie które dzielą zmienne. Rozważmy na przykład CSP ze zmiennymi X = {X,Y,Z}, każda z dziedziną {1,2,3,4,5} i dwoma ograniczeniami C1 : <(X,Y,Z) ,X + Y=Z> i C2 : <(X,Y),X +1 = Y .Wtedy graf dualny miałby zmienne X = {C1,C2} , gdzie domena C1 zmienna w grafie dualnym jest zbiorem {(xi,yj,zk)} krotek z ograniczenia C1 w pierwotnym problemie i podobnie dziedzina C2 jest zbiorem krotek {(xi,yj)}. Wykres dualny ma ograniczenie binarne <(C1,C2), R1), gdzie R1 jest nową relacją, która definiuje ograniczenie między C1 i C2 ; w tym przypadku byłoby to

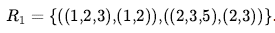
Istnieją jednak dwa powody, dla których możemy preferować globalne ograniczenie, takie jak Alldiff, zamiast zestawu ograniczeń binarnych. Po pierwsze, łatwiej i mniej podatne na błędy jest napisanie opisu problemu za pomocą Alldiff . Po drugie, możliwe jest zaprojektowanie algorytmów wnioskowania specjalnego przeznaczenia dla globalnych ograniczeń, które są bardziej wydajne niż działanie z ograniczeniami pierwotnymi.

Wszystkie opisane przez nas dotychczas ograniczenia były ograniczeniami bezwzględnymi, których naruszenie wyklucza potencjalne rozwiązanie. Wiele rzeczywistych dostawców CSP zawiera ograniczenia preferencji wskazujące, które rozwiązania są preferowane. Na przykład, w uniwersyteckim problemie planowania zajęć istnieją bezwzględne ograniczenia, że ​​żaden profesor nie może uczyć dwóch klas jednocześnie. Ale możemy również dopuścić ograniczenia preferencji: prof. R może preferować nauczanie rano, podczas gdy prof. N woli nauczać po południu. Harmonogram, w którym prof. R naucza o godz. nadal byłoby rozwiązaniem dopuszczalnym (chyba że prof. R jest przewodniczącym wydziału), ale nie optymalnym.

Fabryki mają problem z planowaniem dziennej liczby prac, z zastrzeżeniem różnych ograniczeń. W praktyce wiele z tych problemów rozwiązuje się za pomocą technik CSP. Rozważ problem planowania montażu samochodu. Całe zadanie składa się z zadań, a każde zadanie możemy modelować jako zmienną, gdzie wartością każdej zmiennej jest czas rozpoczęcia zadania wyrażony jako całkowita liczba minut. Ograniczenia mogą zakładać, że jedno zadanie musi wystąpić przed drugim — na przykład przed założeniem kołpaka należy zamontować koło — i że tylko tyle zadań może być wykonywanych jednocześnie. Ograniczenia mogą również określać, że wykonanie zadania zajmuje określoną ilość czasu. Rozważamy niewielką część montażu samochodu, składającego się z 15 zadań: montaż osi (przedniej i tylnej), przymocuj wszystkie cztery koła (prawe i lewe, przednie i tylne), dokręć nakrętki na każdym kole, przymocuj kołpaki i sprawdź końcowy montaż. Zadania możemy przedstawić za pomocą 15 zmiennych:

Następnie przedstawiamy ograniczenia pierwszeństwa między poszczególnymi zadaniami. Ilekroć zadanie T₁ musi nastąpić przed zadaniem T₂ , a zadanie T₁ trwa d₁ do wykonania, dodajemy ograniczenie arytmetyczne postaci

W naszym przykładzie osie muszą być na swoim miejscu przed założeniem kół, a montaż osi zajmuje 10 minut, więc piszemy

Następnie mówimy, że do każdego koła musimy przymocować koło (co zajmuje 1 minutę), następnie dokręcić nakrętki (2 minuty), a na koniec założyć kołpak (1 minuta, ale jeszcze nie przedstawiony):

Załóżmy, że mamy czterech pracowników do montażu kół, ale muszą dzielić jedno narzędzie, które pomaga umieścić oś na miejscu. Potrzebujemy ograniczenia rozłącznego, aby powiedzieć, że Axle_F i Axle_B nie mogą się pokrywać w czasie; albo jeden jest pierwszy, albo drugi:

Wygląda to na bardziej skomplikowane ograniczenie, łączące arytmetykę i logikę. Ale nadal sprowadza się do zestawu par wartości AxleF i AxleB , które  mogą przyjąć. Musimy również zapewnić, że inspekcja jest ostatnia i trwa 3 minuty. Dla każdej zmiennej z wyjątkiem Inspect dodajemy ograniczenie postaci

Na koniec załóżmy, że istnieje potrzeba wykonania całego montażu w 30 minut. Możemy to osiągnąć, ograniczając domenę wszystkich zmiennych:

D_i = {0,1,2,3…30}

Ten konkretny problem jest trywialny do rozwiązania, ale CSP zostały z powodzeniem zastosowane do takich problemów z harmonogramem warsztatów z tysiącami zmiennych.

Załóżmy, że znudziwszy się Rumunią, patrzymy na mapę Australii przedstawiającą każdy z jej stanów i terytoriów (rysunek (a) ). Otrzymujemy zadanie pokolorowania każdego regionu na czerwono, zielono lub niebiesko w taki sposób, aby żadne dwa sąsiadujące regiony nie miały tego samego koloru. Aby sformułować to jako CSP, definiujemy zmienne jako regiony:

X = {WA,NT,Q,NSW,V,SA,T}.

Domeną każdej zmiennej jest zbiór  Ograniczenia wymagają sąsiadujących regionów aby miały wyraźne kolory. Ponieważ istnieje dziewięć miejsc graniczących z regionami, istnieje dziewięć ograniczeń:

Tutaj używamy skrótów; SA ≠ WA jest skrótem do <(SA,WA),SA ≠ WA) , gdzie SA ≠ WA można z kolei w pełni wyliczyć jako

Istnieje wiele możliwych rozwiązań tego problemu, takich jak:

Pomocna może być wizualizacja CSP jako wykresu ograniczeń, jak pokazano na rysunku (b). Węzły grafu odpowiadają zmiennym problemu, a krawędź łączy dowolne dwie zmienne, które uczestniczą w ograniczeniu.

Po co formułować problem jako CSP? Jednym z powodów jest to, że CSP dają naturalną reprezentację szerokiej gamy problemów; często łatwo jest sformułować problem jako CSP. Innym jest to, że lata prac rozwojowych zajęły szybkie i wydajne rozwiązania CSP. Trzecim jest to, że solwer CSP może szybko przyciąć duże połacie przestrzeni poszukiwań, czego nie jest w stanie przeszukiwać atomowej przestrzeni stanów. Na przykład, po wybraniu {SA = blue} w problemie Australii, możemy stwierdzić, że żadna z pięciu sąsiednich zmiennych nie może przyjąć wartości blue . Procedura wyszukiwania, która nie wykorzystuje ograniczeń, musiałaby: rozważ 3⁵ = 243 przypisania dla pięciu sąsiednich zmiennych; z ograniczeniami mamy do rozważenia tylko 2⁵ = 32 zadania, co oznacza redukcję o 87%. W przeszukiwaniu atomowej przestrzeni stanów możemy tylko zapytać: czy ten konkretny stan jest celem? Nie? A co z tym? W przypadku dostawców CSP, gdy dowiemy się, że przypisanie częściowe narusza ograniczenie, możemy natychmiast odrzucić dalsze udoskonalenia przypisania częściowego. Co więcej, możemy zobaczyć, dlaczego przypisanie nie jest rozwiązaniem — widzimy, które zmienne naruszają ograniczenie — dzięki czemu możemy skupić uwagę na zmiennych, które mają znaczenie. W rezultacie wiele problemów, które są trudne do rozwiązania w przypadku przeszukiwania atomowej przestrzeni stanów, można szybko rozwiązać, gdy zostaną sformułowane jako CSP.

Problem spełnienia więzów składa się z trzech komponentów, X,D i C :

X to zbiór zmiennych {X₁…X_n}.

D jest zbiorem domen,{D₁…D_n} , po jednej dla każdej zmiennej.

C to zestaw ograniczeń, które określają dopuszczalne kombinacje wartości.

Dziedzina D składa się ze zbioru dopuszczalnych wartości {v₁…v_n} dla zmiennej X_i. Na przykład zmienna logiczna miałaby domenę {true,false}. Różne zmienne mogą mieć różne domeny o różnych rozmiarach. Każde ograniczenie C składa się z pary <scope, rel>, gdzie scope jest krotką zmiennych uczestniczących w ograniczeniu, a rel jest relacją definiującą wartości, które te zmienne mogą przyjąć. Relacja może być reprezentowana jako jawny zestaw wszystkich krotek wartości, które spełniają ograniczenie, lub jako funkcja, która może obliczyć, czy krotka jest członkiem relacji. Na przykład, jeśli X₁ i X₂ mają domenę {1,2,3}, to ograniczenie mówiące, że X₁ musi być większe niż X₂ można zapisać jako  lub jako

Pokażemy jak traktowanie stanów jako czegoś więcej niż tylko małych czarnych skrzynek prowadzi do nowych metod wyszukiwania i głębszego zrozumienia struktury problemu. Badaliśmy ideę, że problemy można rozwiązać, przeszukując przestrzeń stanów: graf, w którym węzły są stanami, a krawędzie między nimi są działaniami. Widzieliśmy, że heurystyki specyficzne dla domeny mogą oszacować koszt osiągnięcia celu z danego stanu, ale z punktu widzenia algorytmu wyszukiwania każdy stan jest atomowy, czyli niepodzielny – czarna skrzynka bez wewnętrznej struktury. Dla każdego problemu potrzebujemy kodu specyficznego dla domeny, aby opisać przejścia między stanami.

Otwieramy czarną skrzynkę, używając reprezentacji każdego stanu na czynniki: zestawu zmiennych, z których każda ma wartość. Problem rozwiązuje się, gdy każda zmienna ma wartość, która spełnia wszystkie ograniczenia nałożone na zmienną. Tak opisany problem nazywa się problemem spełniania ograniczeń lub CSP. Algorytmy wyszukiwania CSP wykorzystują strukturę stanów i wykorzystują heurystykę ogólną, a nie dziedzinową, aby umożliwić rozwiązywanie złożonych problemów. Główną ideą jest eliminacja dużych części przestrzeni wyszukiwania za jednym razem poprzez identyfikację kombinacji zmiennych/wartości, które naruszają ograniczenia. Dostawcy CSP mają tę dodatkową zaletę, że model działań i przejścia można wywnioskować z opisu problemu.

Przyjrzeliśmy się różnym grom, aby zrozumieć, co oznacza optymalna gra, aby zrozumieć, jak dobrze grać w praktyce i aby wyczuć, jak agent powinien zachowywać się w dowolnym środowisku przeciwnika. Najważniejsze pomysły to:

* Grę można zdefiniować na podstawie stanu początkowego (w jaki sposób jest ustawiona plansza), czynności prawnych w każdym stanie, wyniku każdego działania, testu końcowego (który mówi, kiedy gra się kończy) oraz funkcji użyteczności, która dotyczy stanów końcowych, aby powiedzieć, kto wygrał i jaki jest ostateczny wynik.

* W dwuosobowych, dyskretnych, deterministycznych grach o sumie zerowej, obejmujących turę, z doskonałymi informacjami, algorytm minimax może wybrać optymalne ruchy, wyliczając najpierw głębię drzewa gry.

* Algorytm wyszukiwania alfa-beta oblicza ten sam optymalny ruch, co minimaks, ale osiąga znacznie większą wydajność, eliminując poddrzewa, które nie mają znaczenia.

* Zwykle nie jest możliwe uwzględnienie całego drzewa gry (nawet w przypadku alfa-beta), więc w pewnym momencie musimy przerwać wyszukiwanie i zastosować heurystyczną funkcję oceny, która oszacowuje użyteczność stanu.

* Alternatywa zwana przeszukiwaniem drzewa Monte Carlo (MCTS) ocenia stany nie przez zastosowanie funkcji heurystycznej, ale poprzez rozegranie gry do końca i użycie reguł gry, aby zobaczyć, kto wygrał. Ponieważ ruchy wybrane podczas rozgrywki mogły nie być ruchami optymalnymi, proces jest powtarzany wiele razy, a ocena jest średnią wyników.

* Wiele programów do gier wstępnie oblicza tabele najlepszych ruchów na początku i na końcu gry, aby móc wyszukać ruch zamiast szukać.

* Gry losowe mogą być obsługiwane przez expectiminimax, rozszerzenie algorytmu minimax, który ocenia węzeł losowy, biorąc średnią użyteczność wszystkich jego dzieci, ważoną prawdopodobieństwem każdego dziecka.

* W grach z niedoskonałymi informacjami, takich jak Kriegspiel i poker, optymalna gra wymaga rozumowania na temat obecnego i przyszłego stanu przekonań każdego gracza. Proste przybliżenie można uzyskać, uśredniając wartość akcji dla każdej możliwej konfiguracji brakujących informacji.

* Programy solidnie pokonały mistrzów ludzkich graczy w szachy, warcaby, Othello, Go, pokera i wiele innych gier. Ludzie zachowują przewagę w kilku grach z niedoskonałymi informacjami, takich jak brydż czy Kriegspiel. W grach wideo, takich jak StarCraft i Dota 2, programy konkurują z ludzkimi ekspertami, ale część ich sukcesu może wynikać z ich zdolności do bardzo szybkiego wykonywania wielu czynności.

Ponieważ obliczanie optymalnych decyzji w złożonych grach jest trudne, wszystkie algorytmy muszą dokonywać pewnych założeń i przybliżeń. Wyszukiwanie alfa-beta wykorzystuje funkcję oceny heurystycznej jako przybliżenie, a wyszukiwanie Monte Carlo oblicza przybliżoną średnią z losowego wyboru odtworzeń. Wybór algorytmu zależy po części od cech każdej gry: gdy współczynnik rozgałęzienia jest wysoki lub trudno jest zdefiniować funkcję oceny, preferowane jest przeszukiwanie metodą Monte Carlo. Ale oba algorytmy mają podstawowe ograniczenia. Jednym z ograniczeń wyszukiwania alfa-beta jest jego podatność na błędy w funkcji heurystycznej. Rysunek 5.16 pokazuje dwuwarstwowe drzewo gry, dla którego minimax sugeruje wybranie prawej gałęzi , ponieważ 100 > 99

To jest właściwy ruch, jeśli oceny są dokładnie dokładne. Załóżmy jednak, że ocena każdego węzła zawiera błąd, który jest niezależny od innych węzłów i jest losowo rozłożony z odchyleniem standardowym równym . Wtedy lewa gałąź jest w rzeczywistości lepsza w 71% przypadków, kiedy σ = 5 , i 58% przypadków, kiedy σ = 2  (ponieważ jeden z czterech liści po prawej stronie prawdopodobnie spadnie poniżej 99 w tych przypadkach). Jeżeli błędy w funkcji oceny nie są niezależne, wzrasta prawdopodobieństwo popełnienia błędu. Trudno to zrekompensować, ponieważ nie mamy dobrego modelu zależności między wartościami węzłów rodzeństwa.

Drugim ograniczeniem zarówno alfa-beta, jak i Monte Carlo jest to, że są one zaprojektowane do obliczania (ograniczenia) wartości dozwolonych ruchów. Ale czasami jest jeden ruch, który jest oczywiście najlepszy (na przykład, gdy jest tylko jeden prawidłowy ruch), a w takim przypadku nie ma sensu tracić czasu na obliczenie wartości ruchu – lepiej po prostu wykonać ruszaj się. Lepszy algorytm wyszukiwania wykorzystywałby ideę użyteczności rozwinięcia węzła, wybierając rozwinięcia węzłów o wysokiej użyteczności, to znaczy takie, które prawdopodobnie doprowadzą do odkrycia znacznie lepszego ruchu. Jeśli nie ma rozszerzeń węzłów, których użyteczność jest wyższa niż ich koszt (w ujęciu czasowym), algorytm powinien przerwać wyszukiwanie i wykonać ruch. Działa to nie tylko w przypadku wyraźnych ulubionych sytuacji, ale także w przypadku ruchów symetrycznych, dla których żadna ilość poszukiwań nie pokaże, że jeden ruch jest lepszy od drugiego. Ten rodzaj rozumowania na temat tego, co należy zrobić z obliczeniami, nazywa się metarozumowaniem (rozumowaniem na temat rozumowania). Odnosi się to nie tylko do grania w gry, ale do wszelkiego rodzaju rozumowania. Wszystkie obliczenia są wykonywane w celu podjęcia lepszych decyzji, wszystkie wiążą się z pewnymi kosztami i wszystkie mają pewne prawdopodobieństwo uzyskania pewnej poprawy jakości decyzji. Wyszukiwanie metodą Monte Carlo próbuje przeprowadzić metarozumowanie w celu przydzielenia zasobów do najważniejszych części drzewa, ale nie robi tego w optymalny sposób.

Trzecim ograniczeniem jest to, że zarówno alfa-beta, jak i Monte Carlo wykonują wszystkie swoje rozumowanie na poziomie poszczególnych ruchów. Oczywiście ludzie grają w gry inaczej: mogą rozumować na bardziej abstrakcyjnym poziomie, biorąc pod uwagę cel wyższego poziomu – na przykład schwytanie królowej przeciwnika – i wykorzystując go do selektywnego generowania prawdopodobnych planów. W rozdziale 11 przestudiujemy ten rodzaj planowania, aw rozdziale 11.4 pokażemy, jak planować z hierarchią abstrakcyjnych do konkretnych reprezentacji. Czwartą kwestią jest możliwość włączenia uczenia maszynowego do procesu wyszukiwania gier. Wczesne programy gier opierały się na ludzkiej wiedzy, aby tworzyć funkcje oceny rękodzieła, otwieranie książki, strategie wyszukiwania i triki wydajnościowe. Dopiero zaczynamy dostrzegać programy takie jak ALPHAZERO (Silver i in., 2018), które opierały się na uczeniu maszynowym na podstawie samodzielnej gry, a nie na wiedzy stworzonej przez człowieka związanej z grą.

Gry karciane, takie jak brydż, wist, kiery i poker, cechują się stochastyczną częściową obserwowalnością, w której brakujące informacje są generowane przez losowe rozdanie kart. Na pierwszy rzut oka może się wydawać, że te gry karciane są jak gry w kości: karty są rozdawane losowo i określają ruchy dostępne dla każdego gracza, ale wszystkie „kostki” są rzucane na początku! Mimo że ta analogia okazuje się błędna, sugeruje algorytm: traktuj początek gry jako węzeł szansy z każdą możliwą transakcją jako wynikiem, a następnie użyj formuły EXPECTIMINIMAX, aby wybrać najlepszy ruch. Zauważ, że w tym podejściu jedynym węzłem szansy jest węzeł główny; po tym gra staje się w pełni obserwowalna. Takie podejście jest czasami nazywane uśrednianiem względem jasnowidzenia, ponieważ zakłada, że ​​po zawarciu faktycznego porozumienia gra staje się w pełni obserwowalna dla obu graczy. Pomimo intuicyjnego uroku strategia może sprowadzić na manowce. Rozważ następującą historię:

DZIEŃ 1: Droga A prowadzi do garnka ze złotem; Droga B prowadzi do rozwidlenia. Widać, że lewy widelec prowadzi do dwóch garnków złota, a prawy prowadzi do przejechania przez autobus.

DZIEŃ 2: Droga A prowadzi do garnka złota; Droga B prowadzi do rozwidlenia. Widać, że prawe rozwidlenie prowadzi do dwóch garnków złota, a lewe do najechania autobusem.

DZIEŃ 3: Droga A prowadzi do garnka złota; Droga B prowadzi do rozwidlenia. Powiedziano ci, że jeden widelec prowadzi do dwóch garnków złota, a jeden widelec prowadzi do przejechania przez autobus. Niestety nie wiesz, który widelec jest który.

Uśrednianie względem jasnowidzenia prowadzi do następującego rozumowania: w dniu 1 B jest właściwym wyborem; w dniu 2 B jest właściwym wyborem; w Dniu 3 sytuacja jest taka sama jak w Dniu 1 lub Dniu 2, więc B nadal musi być właściwym wyborem. Teraz możemy zobaczyć, jak zawodzi uśrednianie względem jasnowidzenia: nie uwzględnia ono stanu przekonania, w którym agent znajdzie się po działaniu. Stan wiary w całkowitą ignorancję nie jest pożądany, zwłaszcza gdy jedną z możliwości jest pewna śmierć. Ponieważ zakłada, że ​​każdy przyszły stan będzie automatycznie stanem doskonałej wiedzy, podejście jasnowidzenia nigdy nie wybiera działań, które zbierają informacje (jak pierwszy ruch na rysunku powyżej); nie wybierze też działań, które ukrywają informacje przed przeciwnikiem lub dostarczają informacji partnerowi, ponieważ zakłada, że ​​już zna te informacje; i nigdy nie blefuje w pokerze, ponieważ zakłada, że ​​przeciwnik widzi jego karty. W rozdziale 17 pokazujemy, jak konstruować algorytmy, które wykonują wszystkie te rzeczy dzięki rozwiązaniu prawdziwego, częściowo obserwowalnego problemu decyzyjnego, co skutkuje optymalną strategią równowagi. Pomimo wad, uśrednianie względem jasnowidzenia może być skuteczną strategią, z kilkoma sztuczkami, które sprawią, że będzie działać lepiej. W większości gier karcianych liczba możliwych rozdań jest dość duża. Na przykład w grze w brydża każdy gracz widzi tylko dwa z czterech rozdań; są dwie niewidoczne ręce po 13 kart każda, więc liczba rozdań wynosi 

Rozwiązanie nawet jednego rozdania jest dość trudne, więc rozwiązanie dziesięciu milionów nie wchodzi w rachubę. Jednym ze sposobów radzenia sobie z tą ogromną liczbą jest abstrakcja, czyli traktowanie podobnych rąk jako identycznych. Na przykład bardzo ważne jest, które asy i króle są w rozdaniu, ale to, czy w rozdaniu jest 4 czy 5, nie jest tak ważne i można je oddzielić.

Innym sposobem radzenia sobie z dużą liczbą jest przycinanie do przodu: rozważ tylko małą losową próbkę N transakcji i ponownie oblicz wynik EXPECTIMINIMAX. Nawet dla dość małego N – powiedzmy 100 do 1000 – ta metoda daje dobre przybliżenie. Można go również zastosować do gier deterministycznych, takich jak Kriegspiel, w których próbkujemy możliwe stany gry, a nie możliwe transakcje, o ile mamy jakiś sposób na oszacowanie prawdopodobieństwa każdego stanu. Pomocne może być również wyszukiwanie heurystyczne z odcięciem głębokości zamiast przeszukiwania całego drzewa gry. Do tej pory zakładaliśmy, że każda transakcja jest równie prawdopodobna. Ma to sens w przypadku gier takich jak wista i kiery. Ale w brydżu grę poprzedza faza licytacji, w której każda drużyna wskazuje, ile lew spodziewa się wygrać. Ponieważ gracze licytują na podstawie posiadanych kart, pozostali gracze dowiadują się czegoś o prawdopodobieństwie P(s) każdego rozdania. Wzięcie tego pod uwagę przy podejmowaniu decyzji, jak rozegrać rozdanie, jest trudne z powodów wymienionych w naszym opisie Kriegspiel: gracze mogą licytować w taki sposób, aby zminimalizować informacje przekazywane swoim przeciwnikom. Komputery osiągnęły w pokerze wydajność nadludzką. Program pokerowy Libratus pokonał czterech najlepszych pokerzystów na świecie w 20-dniowym meczu Texas Hold’em bez limitu i zdecydowanie pokonał ich wszystkich. Ponieważ w pokerze jest tak wiele możliwych stanów, Libratus używa abstrakcji, aby zredukować przestrzeń stanów: może uznać, że dwie ręce AAA72 i AAA64 są równoważne (oba są „trzema asami i kilkoma niskimi kartami”) i może rozważyć zakład w wysokości 200 dolarów będzie taki sam jak 201 dolarów. Ale Libratus monitoruje również innych graczy i jeśli wykryje, że wykorzystują abstrakcję, wykona dodatkowe obliczenia w nocy, aby zatkać tę dziurę. Łącznie zużył 25 milionów godzin pracy procesora na superkomputerze, aby odnieść zwycięstwo. Koszty obliczeniowe poniesione przez Libratus (i podobne koszty przez ALPHAZERO i inne systemy) sugerują, że gra o mistrza świata może nie być osiągalna dla naukowców z ograniczonymi budżetami. W pewnym stopniu jest to prawdą: tak jak nie powinieneś oczekiwać, że będziesz w stanie złożyć mistrzowski samochód wyścigowy Formuły 1 z części zamiennych w swoim garażu, zaletą jest dostęp do superkomputerów lub specjalistycznego sprzętu, takiego jak Tensor Processing Units. Jest to szczególnie prawdziwe w przypadku szkolenia systemu, ale szkolenie można również przeprowadzić za pośrednictwem crowdsourcingu. Na przykład system LEELAZERO o otwartym kodzie źródłowym jest reimplementacją ALPHAZERO, która trenuje poprzez samodzielną zabawę na komputerach uczestników-wolontariuszy. Po przeszkoleniu wymagania obliczeniowe dla rzeczywistej gry turniejowej są skromne. ALPHASTAR wygrał gry StarCraft II działające na zwykłym komputerze stacjonarnym z pojedynczym procesorem graficznym, a ALPHAZERO mogło działać w tym trybie.

Zasady Kriegspiel są następujące: każdy biały i czarny widzą planszę zawierającą tylko własne pionki. Sędzia, który widzi wszystkie figury, rozstrzyga mecz i okresowo wydaje komunikaty, które są słyszane przez obu graczy. Po pierwsze, biały proponuje sędziemu posunięcie, które byłoby legalne, gdyby nie było czarnych figur. Jeśli czarne bierki zapobiegną ruchowi, sędzia ogłasza „nielegalne”, a białe proponują ruchy, dopóki nie zostanie znaleziony legalny – dowiadują się więcej o lokalizacji bierek czarnych w tym procesie. Po zaproponowaniu legalnego posunięcia sędzia ogłasza jedną lub więcej z następujących czynności:

„Bicie na polu X”, jeśli doszło do bicia, i „Szach przez D”, jeśli czarny król jest szachowany, gdzie D jest kierunkiem szachu i może być jednym z „skoczek”, „rangi”, „pliku”. ”, „Długa przekątna” lub „Krótka przekątna”. Jeżeli czarne są zamatowane lub patowe, sędzia o tym mówi; w przeciwnym razie kolej na ruch czarnych. Kriegspiel może wydawać się przerażająco niemożliwy, ale ludzie radzą sobie z nim całkiem dobrze i programy komputerowe zaczynają nadrabiać zaległości. Pomaga przywołać pojęcie stanu przekonań – zbiór wszystkich logicznie możliwych stanów tablicy, biorąc pod uwagę pełną historię dotychczasowych percepcji. Początkowo stan wiary białych jest singletonem, ponieważ pionki czarnych jeszcze się nie poruszyły. Po tym, jak biały wykona ruch i czarny odpowie, stan wiary białych zawiera 20 pozycji, ponieważ czarny ma 20 odpowiedzi na każdy ruch otwierający. Śledzenie stanu przekonania w miarę postępu gry jest właśnie problemem estymacji stanu, dla którego krok aktualizacji jest podany w równaniu. Możemy mapować estymację stanu Kriegspiela bezpośrednio na częściowo obserwowalne, niedeterministyczne ramy sekcji, jeśli uważamy przeciwnika za źródło niedeterminizmu; to znaczy, WYNIKI ruchu białych składają się z (przewidywalnego) wyniku własnego ruchu białych i nieprzewidywalnego wyniku podanego przez odpowiedź czarnych. Biorąc pod uwagę obecny stan przekonań, biały może zapytać: „Czy mogę wygrać grę?” W przypadku częściowo obserwowalnej gry zmienia się pojęcie strategii; zamiast określać ruch dla każdego możliwego ruchu, który może wykonać przeciwnik, potrzebujemy ruchu dla każdej możliwej sekwencji perceptu, która może zostać odebrana. Dla Kriegspiel strategia wygrywająca lub gwarantowany mat to taka, która dla każdej możliwej sekwencji percepcji prowadzi do rzeczywistego mata dla każdego możliwego stanu szachownicy w obecnym stanie przekonania, niezależnie od tego, jak porusza się przeciwnik. Przy tej definicji stan wiary przeciwnika jest nieistotny – strategia musi działać, nawet jeśli przeciwnik widzi wszystkie pionki. To znacznie upraszcza obliczenia. Rysunek pokazuje część gwarantowanego mata w końcówce KRK (król i wieża kontra król).

W tym przypadku czarny ma tylko jedną figurę (króla), więc stan wiary białych można pokazać na pojedynczej planszy, zaznaczając każdą możliwą pozycję czarnego króla.

Ogólny algorytm wyszukiwania AND-OR może być zastosowany do przestrzeni stanów przekonań w celu znalezienia gwarantowanych matów. Przyrostowy algorytm stanu przekonania, często znajduje matów w środkowej fazie gry do głębokości 9 – znacznie powyżej umiejętności większości ludzkich graczy. Oprócz gwarantowanych matów Kriegspiel dopuszcza zupełnie nową koncepcję, która nie ma sensu w grach w pełni obserwowalnych: mat probabilistyczny. Take maty nadal muszą pracować w każdym stanie szachownicy w stanie wiary; są probabilistyczne w odniesieniu do losowości ruchów zwycięskiego gracza. Aby uzyskać podstawową ideę, rozważ problem znalezienia samotnego czarnego króla przy użyciu tylko białego króla. Po prostu poruszając się losowo, biały król w końcu wpadnie na czarnego króla, nawet jeśli ten spróbuje uniknąć tego losu, ponieważ czarne nie mogą w nieskończoność odgadywać właściwych ruchów unikowych. W terminologii teorii prawdopodobieństwa wykrycie występuje z prawdopodobieństwem 1. Koniec gry KBNK – król, goniec i skoczek kontra król – wygrywa w tym sensie; Biały przedstawia czarnemu nieskończoną losową sekwencję wyborów, z których jeden czarny odgadnie błędnie i ujawni swoją pozycję, prowadząc do mata. Z drugiej strony końcówka KBBK wygrywa z prawdopodobieństwem 1-e . Białe mogą wymusić zwycięstwo tylko poprzez pozostawienie jednego ze swoich gońców bez ochrony na jeden ruch. Jeśli czarny znajdzie się we właściwym miejscu i zbije gońca (posunięcie, które byłoby nielegalne, gdyby gońce były chronione), gra jest remisowana. Białe mogą zdecydować się na wykonanie ryzykownego ruchu w jakimś losowo wybranym punkcie w środku bardzo długiej sekwencji, redukując w ten sposób do dowolnie małej stałej, ale nie mogą zredukować do zera. Czasami strategia mata działa dla niektórych stanów szachownicy w obecnym stanie przekonań, ale nie dla innych. Próba takiej strategii może się udać, prowadząc do przypadkowego mata – przypadkowego w tym sensie, że białe nie mogą wiedzieć, że będzie to mat – jeśli bierki czarnych znajdą się we właściwych miejscach. (Większość matów w grach między ludźmi ma tę przypadkową naturę.) Pomysł ten w naturalny sposób prowadzi do pytania, jak prawdopodobne jest, że dana strategia wygra, co z kolei prowadzi do pytania, na ile prawdopodobne jest, że każda plansza obecny stan przekonań to prawdziwy stan planszy. Na pierwszy rzut oka można by zasugerować, że wszystkie stany tablicy w obecnym stanie przekonań są jednakowo prawdopodobne — ale to nie może być właściwe. Rozważmy na przykład stan wiary białych po pierwszym ruchu czarnych w grze. Z definicji (zakładając, że czarny gra optymalnie), czarny musiał zagrać optymalny ruch, więc wszystkim stanom planszy wynikającym z suboptymalnych ruchów należy przypisać prawdopodobieństwo zerowe.

Ten argument też nie jest do końca słuszny, ponieważ celem każdego gracza jest nie tylko przeniesienie pionków na odpowiednie pola, ale także zminimalizowanie informacji, jakie ma przeciwnik na temat ich lokalizacji. Granie jakąkolwiek przewidywalną „optymalną” strategią dostarcza przeciwnikowi informacji. W związku z tym optymalna gra w częściowo obserwowalnych grach wymaga chęci grania nieco losowo. (Dlatego inspektorzy higieny restauracji przeprowadzają wyrywkowe wizyty kontrolne.) To oznacza okazjonalne wybieranie ruchów, które mogą wydawać się „wewnętrznie” słabe, ale zyskują na sile dzięki swojej nieprzewidywalności, ponieważ przeciwnik prawdopodobnie nie przygotował przed nimi żadnej obrony.

Z tych rozważań wydaje się, że prawdopodobieństwa związane ze stanami tablicy w obecnym stanie przekonań można obliczyć tylko przy optymalnej strategii randomizowanej; z kolei obliczenie tej strategii wydaje się wymagać znajomości prawdopodobieństw różnych stanów, w których może znajdować się plansza. Ta zagadka może zostać rozwiązana przez przyjęcie teorii gry dotyczącej rozwiązania równowagi, o czym będziemy mówić dalej w rozdziale 17 . Równowaga określa optymalną strategię losową dla każdego gracza. Obliczanie równowagi jest zbyt kosztowne dla Kriegspiela. Obecnie projektowanie efektywnych algorytmów dla ogólnej gry Kriegspiel jest otwartym tematem badawczym. Większość systemów przeprowadza przewidywanie o ograniczonej głębokości we własnej przestrzeni stanów przekonań, ignorując stan przekonań przeciwnika. Funkcje ewaluacyjne przypominają te z obserwowalnej gry, ale zawierają składnik określający wielkość stanu przekonań – mniejsze jest lepsze! Powrócimy do gier częściowo obserwowalnych pod tematem teorii gier