Miesiąc: październik 2021

Widzieliśmy, jak AC-3 może zredukować domeny zmiennych przed rozpoczęciem wyszukiwania. Ale wnioskowanie może być jeszcze silniejsze w trakcie wyszukiwania: za każdym razem, gdy dokonujemy wyboru wartości zmiennej, mamy zupełnie nową możliwość wnioskowania o nowe redukcje domen na sąsiednich zmiennych. Jedną z najprostszych form wnioskowania jest sprawdzanie w przód. Za każdym razem, gdy zmienna X jest przypisana, proces sprawdzania w przód ustala dla niej spójność łukową: dla każdej nieprzypisanej zmiennej Y, która jest połączona z X przez ograniczenie, usuń z domeny Y każdą wartość, która jest niezgodna z wartością wybraną dla X. Rysunek przedstawia postęp wyszukiwania z wycofywaniem w australijskim CSP ze sprawdzaniem w przód.

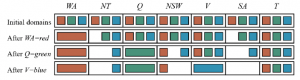
 W tym przykładzie należy zwrócić uwagę na dwie ważne kwestie. Po pierwsze, zauważ, że po przypisaniu WA = czerwony i Q = zielony, domeny NT i SA są zredukowane do jednej wartości; całkowicie wyeliminowaliśmy rozgałęzienia na tych zmiennych poprzez propagowanie informacji z WA i Q. Drugą kwestią, na którą należy zwrócić uwagę, jest to, że po V = blue domena SA jest pusta. Zatem sprawdzanie w przód wykryło, że przypisanie częściowe {WA = czerwony, Q = zielony, V= niebieski} jest niezgodne z ograniczeniami problemu i algorytm natychmiast się cofa.

W przypadku wielu problemów wyszukiwanie będzie skuteczniejsze, jeśli połączymy heurystykę MRV ze sprawdzanie, w przód. Rozważ rysunek  po przypisaniu {WA= red}. Intuicyjnie wydaje się, że to przypisanie ogranicza sąsiadów NT i SA , więc powinniśmy teraz zająć się tymi zmiennymi, a wtedy wszystkie inne zmienne będą się układać. To jest dokładnie to, co dzieje się z MRV: NT i SA mają dwie wartości, więc jedna z nich jest wybierana jako pierwsza, potem druga, a następnie Q, NSW i V w kolejności. Wreszcie T nadal ma trzy wartości i każda z nich działa. Możemy postrzegać sprawdzanie w przód jako skuteczny sposób na przyrostowe obliczanie informacji, których heurystyka MRV potrzebuje do wykonania swojej pracy.

Chociaż sprawdzanie w przód wykrywa wiele niespójności, nie wykrywa ich wszystkich. Problem polega na tym, że nie wybiega wystarczająco daleko w przyszłość. Rozważmy na przykład Q = zielony rząd na Rysunku 6.7 . Uczyniliśmy łuki WA i Q spójnymi, ale zostawiliśmy zarówno NT, jak i SA z kolorem niebieskim jako jedyną możliwą wartością, co jest niespójnością, ponieważ są sąsiadami.

Algorytm o nazwie MAC (for Maintaining Arc Consistency) wykrywa takie niespójności. Po przypisaniu wartości zmiennej Xi procedura INFERENCE wywołuje AC-3, ale zamiast kolejki wszystkich łuków w CSP, zaczynamy tylko od łuków (Xj,Xi) dla wszystkich Xj, które są nieprzypisanymi zmiennymi, które są sąsiadami z . Stamtąd AC-3 propaguje ograniczenia w zwykły sposób, a jeśli jakakolwiek zmienna ma swoją domenę zredukowaną do pustego zestawu, wywołanie AC-3 kończy się niepowodzeniem i wiemy, że należy natychmiast się wycofać. Widzimy, że MAC jest ściślej potężniejszy niż sprawdzanie w przód, ponieważ sprawdzanie w przód robi to samo, co MAC na początkowych łukach w kolejce MAC; ale w przeciwieństwie do MAC, sprawdzanie w przód nie propaguje rekursywnie ograniczeń, gdy wprowadzane są zmiany w domenach zmiennych.

Algorytm cofania zawiera linię. Najprostszą strategią dla SELECT-UNASSIGNED-VARIABLE jest porządkowanie statyczne: wybierz zmienne w kolejności {X1,X2,…}. Następnym najprostszym jest wybór losowy. Żadna strategia nie jest optymalna. Na przykład po przypisaniu WA =red i NT = green na rysunku 6.6 istnieje tylko jedna możliwa wartość dla SA , więc sensowne jest przypisanie SA = blue zamiast przypisywania Q. W rzeczywistości, po przypisaniu SA, wszystkie wybory Q, NSW i Vare są wymuszone. Ten intuicyjny pomysł – wybór zmiennej o najmniejszej „legalnej” wartości – nazywa się heurystyką minimalnych pozostałych wartości (MRV). Została również nazwana „najbardziej ograniczoną zmienną” lub heurystyką „najpierw błąd”, ponieważ wybiera zmienną, która najprawdopodobniej wkrótce spowoduje awarię, tym samym przycinając drzewo wyszukiwania. Jeśli jakaś zmienna X nie ma żadnych legalnych wartości, heurystyka MRV wybierze X, a niepowodzenie zostanie natychmiast wykryte, unikając bezcelowych przeszukiwań innych zmiennych. Heurystyka MRV zwykle działa lepiej niż losowe lub statyczne porządkowanie, czasami o rzędy wielkości, chociaż wyniki różnią się w zależności od problemu. Heurystyka MRV w ogóle nie pomaga w wyborze pierwszego regionu do pokolorowania w Australii, ponieważ początkowo każdy region ma trzy legalne kolory. W takim przypadku przydaje się heurystyka stopni. Próbuje zredukować czynnik rozgałęzienia w przyszłych wyborach, wybierając zmienną, która jest zaangażowana w największą liczbę ograniczeń dla innych nieprzypisanych zmiennych. Na wykresie 6.1 SA jest zmienną o najwyższym stopniu, 5; pozostałe zmienne mają stopień 2 lub 3, z wyjątkiem , który ma stopień 0. W rzeczywistości SA raz wybiera się, stosując stopień heurystyki rozwiązuje problem bez żadnych fałszywych kroków — możesz wybrać dowolny spójny kolor w każdym punkcie wyboru i nadal znaleźć rozwiązanie bez cofania się. Heurystyka minimalnych pozostałych wartości jest zwykle potężniejszą wskazówką, ale heurystyka stopnia może być użyteczna jako rozwiązanie rozstrzygające remisy.

Po wybraniu zmiennej algorytm musi zdecydować o kolejności sprawdzania jej wartości. W tym przypadku skuteczna jest heurystyka o najmniejszej wartości ograniczającej. Preferuje wartość, która wyklucza najmniej możliwości wyboru sąsiednich zmiennych na wykresie ograniczeń. Załóżmy na przykład, że na rysunku 6.1 wygenerowaliśmy częściowe przypisanie z WA=red i NT=green i że nasz następny wybór dotyczy . Niebieski byłby złym wyborem, ponieważ eliminuje ostatnią legalną wartość pozostawioną sąsiadowi Q, SA. Dlatego heurystyka z najmniejszą wartością ograniczającą preferuje kolor czerwony od niebieskiego. Ogólnie rzecz biorąc, heurystyka stara się pozostawić maksymalną elastyczność dla kolejnych przypisań zmiennych. Dlaczego wybór zmiennych miałby być pierwszym niepowodzeniem, a wybór wartości ostatnim niepowodzeniem? Każda zmienna musi być ostatecznie przypisana, więc wybierając te, które prawdopodobnie zawiodą w pierwszej kolejności, będziemy mieli średnio mniej udanych przypisań do cofnięcia się. W przypadku porządkowania wartości sztuczka polega na tym, że potrzebujemy tylko jednego rozwiązania; dlatego warto najpierw poszukać najbardziej prawdopodobnych wartości. Gdybyśmy chcieli wyliczyć wszystkie rozwiązania, a nie tylko je znaleźć, porządkowanie wartości byłoby nieistotne.

Czasami możemy zakończyć proces propagacji ograniczeń i nadal mieć zmienne z wieloma możliwymi wartościami. W takim przypadku musimy poszukać rozwiązania. W tej sekcji omówimy algorytmy wyszukiwania z wycofywaniem, które działają na przypisaniach częściowych; w następnej sekcji przyjrzymy się lokalnym algorytmom wyszukiwania nad pełnymi zadaniami. Zastanów się, jak standardowe wyszukiwanie o ograniczonej głębokości (z rozdziału 3) może rozwiązać CSP. Stan byłby częściowym przypisaniem, a akcja rozszerzyłaby przypisanie, dodając, powiedzmy, NSW = czerwony SA = niebieski lub dla problemu kolorowania mapy Australii. W przypadku dostawcy CSP z n zmiennymi o rozmiarze domeny d otrzymalibyśmy drzewo wyszukiwania, w którym wszystkie kompletne przypisania (a tym samym wszystkie rozwiązania) są węzłami-liśćmi na głębokości . Zauważ jednak, że współczynnik rozgałęzienia na najwyższym poziomie byłby nd, ponieważ dowolne d wartości można przypisać do dowolnej z n zmiennych. Na następnym poziomie współczynnik rozgałęzienia wynosi (n-1) i tak dalej dla n poziomów. Więc drzewo ma n! ∙ dⁿ opuszcza, mimo że istnieją tylko dⁿ możliwe kompletne zadania!

Możemy odzyskać współczynnik n! rozpoznając kluczową właściwość CSP: przemienność. Problem jest przemienny, jeśli kolejność wykonywania danego zbioru działań nie ma znaczenia. W CSP nie ma znaczenia, czy najpierw przypiszemy NSW = red , a następnie SA = blue , czy na odwrót. Dlatego musimy wziąć pod uwagę tylko jedną zmienną w każdym węźle w drzewie wyszukiwania. Na samym początku moglibyśmy dokonać wyboru pomiędzy SA = red , SA = green i SA= blue , ale nigdy nie wybralibyśmy pomiędzy NSW = red i SA =blue. Z tym ograniczeniem, liczba liści wynosi dn , jak mamy nadzieję. Na każdym poziomie drzewa musimy wybrać, z którą zmienną będziemy mieli do czynienia, ale nigdy nie musimy się cofać nad tym wyborem. Rysunek  przedstawia procedurę wyszukiwania z wycofywaniem się dla dostawców CSP.

Wielokrotnie wybiera nieprzypisaną zmienną, a następnie próbuje po kolei wszystkie wartości w domenie tej zmiennej, próbując rozszerzyć każdą z nich na rozwiązanie za pomocą wywołania rekurencyjnego. Jeśli wywołanie się powiedzie, rozwiązanie zostanie zwrócone, a jeśli się nie powiedzie, przypisanie zostanie przywrócone do poprzedniego stanu i spróbujemy następnej wartości. Jeśli żadna wartość nie działa, zwracamy niepowodzenie. Część drzewa wyszukiwania problemu Australii jest pokazana na rysunku  , gdzie przypisaliśmy zmienne w kolejności WA, NT, Q …

Zauważ, że BACKTRACKING-SEARCH zachowuje tylko jedną reprezentację stanu (przypisania) i zmienia tę reprezentację zamiast tworzyć nowe.

Podczas gdy algorytmy wyszukiwania bez informacji można ulepszyć tylko poprzez dostarczenie im heurystyk specyficznych dla domeny, okazuje się, że wyszukiwanie z nawrotem można ulepszyć za pomocą heurystyk niezależnych od domeny, które wykorzystują czynnikową reprezentację CSP. Pokazujemy, jak to się robi.

Popularna łamigłówka Sudoku wprowadziła miliony ludzi w problemy z ograniczaniem satysfakcji, chociaż mogą nie zdawać sobie z tego sprawy. Plansza Sudoku składa się z 81 kwadratów, z których niektóre są początkowo wypełnione cyframi od 1 do 9. Układanka polega na wypełnieniu wszystkich pozostałych kwadratów tak, aby żadna cyfra nie pojawiła się dwa razy w każdym rzędzie, kolumnie lub polu 3 x 3 . Wiersz, kolumna lub pole nazywa się jednostką.

Zagadki Sudoku, które pojawiają się w gazetach i książkach z puzzlami, mają tę właściwość, że istnieje dokładnie jedno rozwiązanie. Chociaż niektóre z nich mogą być trudne do rozwiązania ręcznego, co zajmuje dziesiątki minut, solver CSP może obsłużyć tysiące zagadek na sekundę. Łamigłówkę Sudoku można uznać za CSP z 81 zmiennymi, po jednej dla każdego kwadratu. Używamy nazw zmiennych od A1 do A9 dla górnego rzędu (od lewej do prawej), do I1 do I9 dla dolnego rzędu. Puste kwadraty mają domenę {1,2,3,4,5,6,7,8,9}, a kwadraty wstępnie wypełnione mają domenę składającą się z jednej wartości. Ponadto istnieje 27 różnych ograniczeń Alldiff, po jednym dla każdej jednostki (rzędu, kolumny i pola 9 kwadratów):

Zobaczmy, jak daleko może nas zaprowadzić spójność łuku. Załóżmy, że ograniczenia Alldiff zostały rozszerzone na ograniczenia binarne (takie jak A1 ≠ A2 ), dzięki czemu możemy zastosować AC-3 algorytm bezpośrednio. Rozważ zmienną E6 – pusty kwadrat między 2 i 8 w środkowym polu. Z ograniczeń w pudełku możemy usunąć 1, 2, 7 i 8 z domeny E6. Z ograniczeń w jego kolumnie możemy wyeliminować 5, 6, 2, 8, 9 i 3 (chociaż 2 i 8 zostały już usunięte). To pozostawia E6 z domeną {4} ; innymi słowy, znamy odpowiedź na E6. Rozważmy teraz zmienną I6 – kwadrat w dolnym środkowym polu otoczony przez 1, 3 i 3. Stosując spójność łuku w jego kolumnie, eliminujemy 5, 6, 2, 4 (odkąd wiemy, że E6 musi wynosić 4), 8, 9 i 3. Eliminujemy 1 przez spójność łukową z I5, a zostaje nam tylko wartość 7 w dziedzinie I6. Teraz w kolumnie 6 jest 8 znanych wartości, więc spójność łuku może wywnioskować, że A6 musi wynosić 1. Wnioskowanie jest kontynuowane wzdłuż tych linii i ostatecznie AC-3 może rozwiązać całą zagadkę – wszystkie zmienne mają swoje domeny zredukowane do jednej wartości.

Oczywiście Sudoku wkrótce straciłoby swoją atrakcyjność, gdyby każdą łamigłówkę można było rozwiązać mechanicznie za pomocą AC-3, a AC-3 działa tylko w przypadku najłatwiejszych łamigłówek Sudoku. Nieco trudniejsze można rozwiązać za pomocą PC-2, ale przy większych kosztach obliczeniowych: w łamigłówce Sudoku jest 255 960 różnych ograniczeń ścieżki. Aby rozwiązać najtrudniejsze zagadki i poczynić skuteczne postępy, będziemy musieli być sprytniejsi. Rzeczywiście, atrakcyjność łamigłówek Sudoku dla człowieka rozwiązującego polega na potrzebie zaradności w stosowaniu bardziej złożonych strategii wnioskowania. Miłośnicy nadają im barwne nazwy, takie jak „nagie trójki”. Ta strategia działa w następujący sposób: w dowolnej jednostce (wierszu, kolumnie lub polu) znajdź trzy kwadraty, z których każdy ma domenę zawierającą te same trzy liczby lub podzbiór tych liczb. Na przykład trzy domeny mogą być {1,8}, {3,8} , {1,3,8} . Z tego nie wiemy, który kwadrat zawiera 1, 3 lub 8, ale wiemy, że te trzy liczby muszą być rozdzielone między trzy kwadraty. Dlatego możemy usunąć 1, 3 i 8 z domen co drugiego kwadratu w jednostce. Warto zauważyć, jak daleko możemy się posunąć, nie mówiąc zbyt wiele o tym, co jest specyficzne dla Sudoku. Musimy oczywiście powiedzieć, że istnieje 81 zmiennych, ich domenami są cyfry od 1 do 9 i że istnieje 27 ograniczeń Alldiff. Ale poza tym wszystkie strategie – spójność łuku, spójność ścieżki itd. — mają zastosowanie ogólnie do wszystkich dostawców CSP, a nie tylko do problemów Sudoku. Nawet nagie trójki są tak naprawdę strategią wymuszania spójności ograniczeń i nie są specyficzne dla Sudoku per se. Na tym polega siła formalizmu CSP: dla każdego nowego obszaru problemowego wystarczy zdefiniować problem w kategoriach ograniczeń; wtedy ogólne mechanizmy rozwiązywania ograniczeń mogą przejąć kontrolę.

Pamiętaj, że ograniczenie globalne to takie, które obejmuje dowolną liczbę zmiennych (ale niekoniecznie wszystkie zmienne). Ograniczenia globalne występują często w rzeczywistych problemach i mogą być obsługiwane przez algorytmy specjalnego przeznaczenia, które są bardziej wydajne niż metody ogólnego przeznaczenia opisane do tej pory. Na przykład, ograniczenie Alldiff mówi, że wszystkie zaangażowane zmienne muszą mieć różne wartości (jak w problemie kryptarytmetycznym powyżej i łamigłówce Sudoku poniżej). Jedna prosta forma wykrywania niespójności dla ograniczeń Alldiff działa w następujący sposób: jeśli m zmiennych jest zaangażowanych w ograniczenie i jeśli mają łącznie n możliwych odrębnych wartości, a m > n , to ograniczenie nie może być spełnione. Prowadzi to do następującego prostego algorytmu: Najpierw usuń dowolną zmienną z ograniczenia, która ma domenę singletona i usuń wartość tej zmiennej z domen pozostałych zmiennych. Powtarzaj, dopóki istnieją zmienne singletonowe. Jeśli w dowolnym momencie zostanie utworzona pusta domena lub pozostało więcej zmiennych niż wartości domeny, oznacza to, że wykryto niespójność.

Ta metoda może wykryć niespójność w przypisaniu {WA = red, NSW = red} . Zauważ, że zmienne SA, NT i Q są skutecznie połączone przez ograniczenie Alldiff, ponieważ każda para musi mieć dwa różne kolory. Po zastosowaniu AC-3 z częściowym przypisaniem, wszystkie domeny SA , NT i Q są zredukowane do {green, blue} .

Oznacza to, że mamy trzy zmienne i tylko dwa kolory, więc naruszone jest ograniczenie Alldiff. Tak więc prosta procedura spójności dla ograniczenia wyższego rzędu jest czasami bardziej skuteczna niż zastosowanie spójności łuku do równoważnego zestawu ograniczeń binarnych.

Innym ważnym ograniczeniem wyższego rzędu jest ograniczenie zasobów, czasami nazywane ograniczeniem Atmost. Na przykład, w zadaniu harmonogramowania, niech {P1…P4} oznaczają liczbę personelu przydzielonego do każdego z czterech zadań. Ograniczenie, że nie więcej niż 10 pracowników jest przypisanych w sumie, jest zapisane jako Atmost(10,P1,P2,P3,P4). Możemy wykryć niespójność po prostu sprawdzając sumę minimalnych wartości obecnych domen; na przykład, jeśli każda zmienna ma domenę {3,4,5,6} , ograniczenie Atmost nie może być spełnione. Możemy również wymusić spójność, usuwając maksymalną wartość dowolnej domeny, jeśli nie jest ona zgodna z minimalnymi wartościami innych domen. Zatem jeśli każda zmienna w naszym przykładzie ma domenę {2,3,4,5,6} , wartości 5 i 6 można usunąć z każdej domeny.

W przypadku dużych, ograniczonych zasobów problemów z wartościami całkowitymi — takich jak problemy logistyczne związane z przemieszczaniem tysięcy ludzi w setkach pojazdów — zwykle nie jest możliwe przedstawienie dziedziny każdej zmiennej jako dużego zestawu liczb całkowitych i stopniowe zmniejszanie tego zestawu przez spójność. metody sprawdzania. Zamiast tego domeny są reprezentowane przez górną i dolną granicę i są zarządzane przez propagację granic. Na przykład w problemie z rozkładem lotów załóżmy, że są dwa loty F₁ i F₂, dla których samoloty mają pojemności odpowiednio 165 i 385. Początkowe domeny dla liczby pasażerów w lotach i F₂ to:

Załóżmy teraz, że mamy dodatkowe ograniczenie polegające na tym, że oba loty razem muszą przewozić 420 osób: . Propagując ograniczenia granic, redukujemy domeny do

Mówimy, że CSP jest spójny z granicami, jeśli dla każdej zmiennej X oraz dla wartości dolnej i górnej granicy X istnieje pewna wartość Y, która spełnia ograniczenia między X i Y dla każdej zmiennej. Ten rodzaj propagacji granic jest szeroko stosowany w praktycznych problemach z ograniczeniami.

Silniejsze formy propagacji można zdefiniować pojęciem -konsystencja. CSP jest k-spójny, jeśli dla dowolnego zestawu k-1 zmiennych i dla dowolnego spójnego przypisania do tych zmiennych, spójną wartość można zawsze przypisać dowolnej th zmiennej. 1-konsystencja mówi, że przy danym zbiorze pustym możemy uczynić spójnym dowolny zbiór jednej zmiennej: to właśnie nazwaliśmy spójnością węzłów. Konsystencja 2 jest taka sama jak konsystencja łuku. W przypadku wykresów z ograniczeniami binarnymi 3-spójność jest taka sama jak spójność ścieżki.

CSP jest silnie k-spójny, jeśli jest (k-1)-spójny, a także (k-2)-spójny …, aż do 1-spójny. Załóżmy teraz, że mamy CSP z n węzłami i uczynimy go silnie n-spójnym (tj. silnie k-spójnym dla k = n). Możemy wtedy rozwiązać problem w następujący sposób: Najpierw wybieramy stałą wartość dla X₁. Mamy wtedy gwarancję, że będziemy mogli wybrać wartość dla X2, ponieważ wykres jest 2-spójny, dla X₃, ponieważ jest 3-spójny i tak dalej. Dla każdej zmiennej Xi wystarczy przeszukać wartości d w dziedzinie, aby znaleźć wartość zgodną z X_i…X_i-1 . Całkowity czas działania to tylko O(n²d).

Oczywiście nie ma darmowego obiadu: spełnianie ograniczeń jest ogólnie NP-zupełne, a każdy algorytm ustalania n-spójności musi w najgorszym przypadku zająć czas wykładniczy w n. Co gorsza, n-spójność wymaga również przestrzeni, która jest wykładnicza w n. W praktyce określenie odpowiedniego poziomu sprawdzania spójności jest w większości nauką empiryczną. Obliczanie ze spójności 2 jest powszechne, a ze spójności 3 rzadziej.

Załóżmy, że mamy pokolorować mapę Australii tylko dwoma kolorami, czerwonym i niebieskim. Spójność łuku nic nie daje, ponieważ każde ograniczenie może być indywidualnie spełnione przez kolor czerwony na jednym końcu i niebieski na drugim. Ale najwyraźniej nie ma rozwiązania problemu: ponieważ Australia Zachodnia, Terytorium Północne i Australia Południowa stykają się ze sobą, potrzebujemy co najmniej trzech kolorów dla nich samych. Spójność łuku zacieśnia domeny (ograniczenia jednoargumentowe) za pomocą łuków (ograniczenia binarne). Aby poczynić postępy w takich problemach, jak kolorowanie mapy, potrzebujemy silniejszego pojęcia spójności. Spójność ścieżki zaostrza ograniczenia binarne przy użyciu niejawnych ograniczeń, które są wywnioskowane na podstawie trójek zmiennych.

Zbiór dwóch zmiennych {xi,X_j} jest zgodny ze ścieżką względem trzeciej zmiennej X_m, jeśli dla każdego przypisania {Xi =a , Xj = b} jest zgodny z ograniczeniami (jeśli występują) na {X_i,X_j} , istnieje przypisanie do X_m, które spełnia ograniczenia :X_i,X_m}i {X_m,X_j}. Nazwa odnosi się do ogólnej spójności ścieżki od X_i do X_j z X_m pośrodku. Zobaczmy, jak spójność ścieżki wypada w kolorowaniu mapy Australii dwoma kolorami. Upewnimy się, że zbiór {WA,SA} będzie zgodny ze ścieżką względem NT . Zaczynamy od wyliczenia

spójne przyporządkowania do zestawu. W tym przypadku są tylko dwa: {WA = red , SA = blue} i {WA = blue , SA = red}. Widzimy, że przy obu tych przypisaniach NT nie może być ani czerwone, ani niebieskie (ponieważ kolidowałoby z WA lub SA ). Ponieważ nie ma poprawnego wyboru dla NT , eliminujemy oba przypisania i kończymy bez poprawnych przypisań dla {WA,SA} . Dlatego wiemy, że nie ma rozwiązania tego problemu.

Zmienna w CSP jest spójna łukowo, jeśli każda wartość w jej domenie spełnia ograniczenia binarne zmiennej. Bardziej formalnie Xi, jest łukowo spójne w odniesieniu do innej zmiennej Xj, jeśli dla każdej wartości w bieżącej dziedzinie Di istnieje jakaś wartość w dziedzinie Dj, która spełnia binarne ograniczenie łuku (Xi, Xj). Wykres jest zgodny łukowo, jeśli każda zmienna jest spójna łukowo z każdą inną zmienną. Rozważmy na przykład ograniczenie Y = X², gdzie domena obu i jest zbiorem cyfr dziesiętnych. Możemy napisać to ograniczenie jawnie jako

Aby łuk X był spójny względem , zmniejszamy dziedzinę X do {0,1,2,3} . Jeśli uczynimy arcus-spójny również względem , wtedy domeną , {0,1,4,9} i cały CSP jest arcus-spójny. Z drugiej strony, spójność łuku nie może nic zrobić dla Australii z problemem z kolorowaniem mapy. Rozważ następujące ograniczenie nierówności na (SA,WA):

Bez względu na to, jaką wartość wybierzesz dla SA (lub dla WA ), istnieje prawidłowa wartość dla drugiej zmiennej. Zatem stosowanie spójności łuku nie ma wpływu na domeny żadnej ze zmiennych. Najpopularniejszy algorytm wymuszania spójności łuku nazywa się AC-3 (patrz Rysunek 6.3 ). Aby każda zmienna była spójna, algorytm AC-3 utrzymuje kolejkę łuków do rozważenia. Początkowo kolejka zawiera wszystkie łuki w CSP. (Każde ograniczenie binarne staje się dwoma łukami, po jednym w każdym kierunku.) AC-3 następnie zdejmuje dowolny łuk (Xi,Xj) z kolejki i czyni łuk Xi spójnym względem . Jeśli to pozostawia Di bez zmian, algorytm po prostu przechodzi do następnego łuku. Ale jeśli to zrewiduje Di (zmniejszy domenę), to dodamy do kolejki wszystkie łuki (Xk,Xi), gdzie Xk jest sąsiadem Xi . Musimy to zrobić, ponieważ zmiana w D1 może umożliwić dalsze redukcje Dk , nawet jeśli wcześniej braliśmy pod uwagę Xk. Jeśli Di zostanie zrewidowany do zera, to wiemy, że cały CSP nie ma spójnego rozwiązania, a AC-3 może natychmiast zwrócić niepowodzenie. W przeciwnym razie sprawdzamy, próbując usunąć wartości z domen zmiennych, aż w kolejce nie będzie już żadnych łuków. W tym momencie zostajemy z CSP, który jest równoważny oryginalnemu CSP — oba mają takie same rozwiązania — ale CSP o spójnym łuku będzie szybciej wyszukiwany, ponieważ jego zmienne mają mniejsze domeny. W niektórych przypadkach całkowicie rozwiązuje problem (redukując każdą domenę do rozmiaru 1), a w innych dowodzi, że nie ma rozwiązania (redukując pewną domenę do rozmiaru 0).

Złożoność AC-3 można przeanalizować w następujący sposób. Załóżmy, że dostawca CSP ma n zmiennych, z których każda ma najwyżej rozmiar domeny i ograniczenia binarne (łuki). Każdy łuk (Xk,Xi) może być wstawiony do kolejki tylko raz, ponieważ Xi ma co najwyżej wartości do usunięcia. Sprawdzenie spójności łuku można wykonać w czasie O(d²), więc otrzymujemy całkowity czas najgorszego przypadku O(cd³).

Pojedyncza zmienna (odpowiadająca węzłowi na wykresie CSP) jest zgodna z węzłami, jeśli wszystkie wartości w domenie zmiennej spełniają jednoargumentowe ograniczenia zmiennej. Na przykład w wariancie problemu Australia map-coloring (Rysunek 6.1 ), w którym mieszkańcy Australii nie lubią zieleni, zmienna SA zaczyna się od domeny {red,green,blue} i możemy uczynić ją spójną węzłową, eliminując gee, pozostawiając SA ze zmniejszoną domeną {czerwony,niebieski}. Mówimy, że graf jest spójny węzłowo, jeśli każda zmienna na grafie jest spójna węzłowo. Łatwo jest wyeliminować wszystkie ograniczenia jednoargumentowe w CSP, zmniejszając dziedzinę zmiennych z ograniczeniami jednoargumentowymi na początku procesu rozwiązywania. Jak wspomniano wcześniej, możliwe jest również przekształcenie wszystkich ograniczeń -arowych na binarne. Z tego powodu niektóre solvery CSP działają tylko z ograniczeniami binarnymi, oczekując, że użytkownik z wyprzedzeniem wyeliminuje inne ograniczenia. Przyjmujemy to założenie do końca tego rozdziału, chyba że zaznaczono inaczej.

Algorytm przeszukiwania atomowej przestrzeni stanów czyni postęp tylko w jeden sposób: poprzez rozszerzenie węzła w celu odwiedzenia następców. Algorytm CSP ma wybór. Może generować następniki, wybierając nowe przypisanie zmiennej, lub może wykonać określony rodzaj wnioskowania zwany propagacją ograniczeń: używając ograniczeń do zmniejszenia liczby dopuszczalnych wartości dla zmiennej, co z kolei może zredukować dopuszczalne wartości dla innej zmiennej, i tak dalej. Chodzi o to, aby pozostawić mniej wyborów do rozważenia przy następnym wyborze przypisania zmiennej. Propagacja ograniczeń może być spleciona z wyszukiwaniem lub może być wykonana jako etap przetwarzania wstępnego przed rozpoczęciem wyszukiwania. Czasami to wstępne przetwarzanie może rozwiązać cały problem, więc w ogóle nie jest wymagane wyszukiwanie. Kluczową ideą jest lokalna spójność. Jeśli potraktujemy każdą zmienną jako węzeł w grafie, a każde ograniczenie binarne jako krawędź, to proces wymuszania spójności lokalnej w każdej części grafu powoduje eliminację niespójnych wartości w całym grafie. Istnieją różne rodzaje spójności lokalnej, które z kolei omówimy teraz.