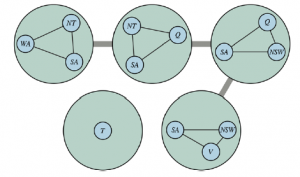
Drugi sposób zredukowania grafu ograniczeń do drzewa opiera się na konstruowaniu dekompozycji drzewa grafu ograniczeń: przekształcenie oryginalnego grafu w drzewo, w którym każdy węzeł w drzewie składa się z zestawu zmiennych, jak na rysunku:
Rozkład drzewa musi spełniać te trzy wymagania:
* Każda zmienna w pierwotnym zadaniu pojawia się w co najmniej jednym z węzłów drzewa.
*Jeżeli dwie zmienne są połączone ograniczeniem w pierwotnym zadaniu, muszą występować razem (wraz z ograniczeniem) w co najmniej jednym z węzłów drzewa.
* Jeśli zmienna pojawia się w dwóch węzłach w drzewie, musi pojawić się w każdym węźle na ścieżce łączącej te węzły.
Pierwsze dwa warunki zapewniają, że wszystkie zmienne i ograniczenia są reprezentowane w dekompozycji drzewa. Trzeci warunek wydaje się dość techniczny, ale pozwala nam powiedzieć, że każda zmienna z pierwotnego problemu musi mieć tę samą wartość, gdziekolwiek się pojawi: ograniczenia w drzewie mówią, że zmienna w jednym węźle drzewa musi mieć taką samą wartość jak odpowiednia zmienna w sąsiednim węźle w drzewie. Na przykład SA pojawia się we wszystkich czterech połączonych węzłach na rysunku 6.13, więc każda krawędź w dekompozycji drzewa zawiera ograniczenie, że wartość SA w jednym węźle musi być taka sama jak wartość SA w następnym. Możesz sprawdzić na rysunku 6.12, że ta dekompozycja ma sens. Gdy mamy już graf o strukturze drzewa, możemy zastosować TREE-CSP-SOLVER, aby uzyskać rozwiązanie w czasie O(nd2), gdzie n jest liczbą węzłów drzewa i rozmiarem największej domeny. Zauważ jednak, że w drzewie domena jest zbiorem krotek wartości, a nie tylko pojedynczymi wartościami. Na przykład lewy górny węzeł na rysunku 6.13 reprezentuje, na poziomie pierwotnego problemu, podproblem ze zmiennymi {WA, NT SA} , domeną {czerwony, zielony, niebieski} i ograniczeniami WA ≠ NT, SA ≠ NT, WA ≠ SA . Na poziomie drzewa węzeł reprezentuje pojedynczą zmienną, którą możemy nazwać SANTWA, której wartością musi być trójka kolorów, np. {czerwony, zielony, niebieski}, ale nie {czerwony, czerwony, niebieski} , ponieważ naruszyłoby to ograniczenie SA ≠ NT z pierwotnego problemu. Następnie możemy przejść z tego węzła do sąsiedniego, ze zmienną, którą możemy nazwać SANTQ i stwierdzić, że istnieje tylko jedna krotka, {czerwona, zielona, niebieska}, która jest zgodna z wyborem dla SANTWA. Dokładnie ten sam proces powtarzamy dla kolejnych dwóch węzłów i niezależnie możemy dokonać dowolnego wyboru dla T . Możemy rozwiązać każdy problem rozkładu drzewa w czasie O(nd2) za pomocą TREE-CSP-SOLVER, który będzie wydajny tak długo, jak d pozostanie małe. Wracając do naszego przykładu ze 100 zmiennymi boolowskimi, jeśli każdy węzeł ma 10 zmiennych, to d = 210 i powinniśmy być w stanie rozwiązać problem w kilka sekund. Ale jeśli istnieje węzeł z 30 zmiennymi, zajęłoby to wieki.
Dany wykres dopuszcza wiele dekompozycji drzewa; przy wyborze rozkładu celem jest jak najmniejsze podproblemy. (Umieszczenie wszystkich zmiennych w jednym węźle jest technicznie drzewem, ale nie jest pomocne). Szerokość drzewa w dekompozycji drzewa grafu jest o jeden mniejsza niż rozmiar największego węzła; szerokość drzewa samego grafu jest zdefiniowana jako minimalna szerokość spośród wszystkich jego dekompozycji drzewa. Jeśli graf ma szerokość drzewa w, to problem można rozwiązać w czasie O(ndw+1) przy odpowiedniej dekompozycji drzewa. Stąd CSP z grafami ograniczeń o ograniczonej szerokości drzewa są rozwiązywalne w czasie wielomianowym. Niestety znalezienie rozkładu przy minimalnej szerokości drzewa jest NP-trudne, ale są metody heurystyczne, które sprawdzają się w praktyce. Co jest lepsze: dekompozycja zestawu przekrojów w czasie O(dc ∙ (nc) lub dekompozycja drzewa w czasie O(ndw+1)? Zawsze, gdy masz zestaw przekrojów cyklicznych o rozmiarze , występuje również szerokość drzewa o rozmiarze w < c+1, a w niektórych przypadkach może być znacznie mniejszy. Więc rozważenie czasu sprzyja dekompozycji drzewa, ale zaletą podejścia cykl-cutset jest to, że może być wykonane w pamięci liniowej, podczas gdy dekompozycja drzewa wymaga pamięci wykładniczej w w