W tej sekcji zbadamy, w jaki sposób struktura problemu, reprezentowana przez wykres ograniczeń, może być wykorzystana do szybkiego znalezienia rozwiązań. Większość z przedstawionych tutaj podejść ma również zastosowanie do innych problemów poza CSP, takich jak rozumowanie probabilistyczne. Jedynym sposobem, w jaki możemy mieć nadzieję na poradzenie sobie z ogromnym światem rzeczywistym, jest rozłożenie go na podproblemy. Patrząc ponownie na wykres ograniczeń dla Australii (rysunek 6.1(b), powtórzony jako rysunek 6.12(a) ), jeden fakt rzuca się w oczy: Tasmania nie jest połączona z lądem. Intuicyjnie jest oczywiste, że pokolorowanie Tasmanii i pokolorowanie lądu są niezależnymi podproblemami – każde rozwiązanie dla lądu połączone z dowolnym rozwiązaniem dla Tasmanii daje rozwiązanie dla całej mapy. Niezależność można ustalić po prostu przez znalezienie połączonych składowych grafu ograniczeń. Każdy składnik odpowiada podproblemowi CSPi. Jeśli przypisanie Si jest rozwiązaniem CSPi , to UiSi jest rozwiązaniem UiCSPi. Dlaczego to jest ważne? Załóżmy, że każdy CSPi ma c zmiennych z łącznej liczby n zmiennych, gdzie c jest stałą. Następnie są podproblemy n/c, z których rozwiązanie wymaga co najwyżej prądu stałego, gdzie jest rozmiarem domeny. Stąd całkowita praca to O(dcn/c) , która jest liniowa w ; bez rozkładu całkowita praca to O(dn) , która jest wykładnicza w n . Zróbmy to bardziej konkretnie: dzielenie a Boolean CSP ze 100 zmiennymi w czterech podproblemach skraca czas rozwiązania najgorszego przypadku z okresu istnienia wszechświata do mniej niż sekundy.
Całkowicie niezależne podproblemy są więc pyszne, ale rzadkie. Na szczęście inne struktury grafów są również łatwe do rozwiązania. Na przykład wykres ograniczeń to drzewo, gdy dowolne dwie zmienne są połączone tylko jedną ścieżką. Pokażemy, że każdy CSP o strukturze drzewa można rozwiązać w czasie liniowo pod względem liczby zmiennych. Kluczem jest nowe pojęcie spójności, zwane kierunkową spójnością łuku lub DAC. CSP jest zdefiniowany jako kierunkowy zgodny łukowo zgodnie z porządkiem zmiennych x1,X2…Xn wtedy i tylko wtedy, gdy każdy Xi jest zgodny łukowo z każdym Xj dla j > i .
Aby rozwiązać problem CSP o strukturze drzewa, najpierw wybierz dowolną zmienną, która będzie korzeniem drzewa, i wybierz kolejność zmiennych w taki sposób, aby każda zmienna pojawiała się po swoim rodzicu w drzewie. Takie uporządkowanie nazywa się sortowaniem topologicznym. Rysunek 6.10(a) przedstawia przykładowe drzewo, a (b) jedną z możliwych kolejności.
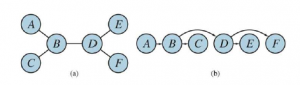
Każde drzewo z n węzłami ma n-1 krawędzi, więc możemy uczynić ten graf ukierunkowany łukowo w O(n) krokach, z których każdy musi porównywać do możliwych wartości domeny dla dwóch zmiennych, dla łącznego czasu O(nd2 ) . Gdy mamy już skierowany wykres zgodny z łukiem, możemy po prostu przejrzeć listę zmiennych i wybrać dowolną pozostałą wartość. Ponieważ każda krawędź od rodzica do jego dziecka jest spójna łukowo, wiemy, że dla dowolnej wartości, którą wybierzemy dla rodzica, pozostanie poprawna wartość do wyboru dla dziecka. Oznacza to, że nie będziemy musieli się cofać; możemy poruszać się liniowo przez zmienne.

Teraz, gdy mamy wydajny algorytm dla drzew, możemy rozważyć, czy bardziej ogólne grafy ograniczeń można jakoś zredukować do drzew. Można to zrobić na dwa sposoby: usuwając węzły lub zwijając węzły razem.