Czasami możemy zakończyć proces propagacji ograniczeń i nadal mieć zmienne z wieloma możliwymi wartościami. W takim przypadku musimy poszukać rozwiązania. W tej sekcji omówimy algorytmy wyszukiwania z wycofywaniem, które działają na przypisaniach częściowych; w następnej sekcji przyjrzymy się lokalnym algorytmom wyszukiwania nad pełnymi zadaniami. Zastanów się, jak standardowe wyszukiwanie o ograniczonej głębokości (z rozdziału 3) może rozwiązać CSP. Stan byłby częściowym przypisaniem, a akcja rozszerzyłaby przypisanie, dodając, powiedzmy, NSW = czerwony SA = niebieski lub dla problemu kolorowania mapy Australii. W przypadku dostawcy CSP z n zmiennymi o rozmiarze domeny d otrzymalibyśmy drzewo wyszukiwania, w którym wszystkie kompletne przypisania (a tym samym wszystkie rozwiązania) są węzłami-liśćmi na głębokości . Zauważ jednak, że współczynnik rozgałęzienia na najwyższym poziomie byłby nd, ponieważ dowolne d wartości można przypisać do dowolnej z n zmiennych. Na następnym poziomie współczynnik rozgałęzienia wynosi (n-1) i tak dalej dla n poziomów. Więc drzewo ma n! ∙ dn opuszcza, mimo że istnieją tylko dn możliwe kompletne zadania!
Możemy odzyskać współczynnik n! rozpoznając kluczową właściwość CSP: przemienność. Problem jest przemienny, jeśli kolejność wykonywania danego zbioru działań nie ma znaczenia. W CSP nie ma znaczenia, czy najpierw przypiszemy NSW = red , a następnie SA = blue , czy na odwrót. Dlatego musimy wziąć pod uwagę tylko jedną zmienną w każdym węźle w drzewie wyszukiwania. Na samym początku moglibyśmy dokonać wyboru pomiędzy SA = red , SA = green i SA= blue , ale nigdy nie wybralibyśmy pomiędzy NSW = red i SA =blue. Z tym ograniczeniem, liczba liści wynosi dn , jak mamy nadzieję. Na każdym poziomie drzewa musimy wybrać, z którą zmienną będziemy mieli do czynienia, ale nigdy nie musimy się cofać nad tym wyborem. Rysunek przedstawia procedurę wyszukiwania z wycofywaniem się dla dostawców CSP.

Wielokrotnie wybiera nieprzypisaną zmienną, a następnie próbuje po kolei wszystkie wartości w domenie tej zmiennej, próbując rozszerzyć każdą z nich na rozwiązanie za pomocą wywołania rekurencyjnego. Jeśli wywołanie się powiedzie, rozwiązanie zostanie zwrócone, a jeśli się nie powiedzie, przypisanie zostanie przywrócone do poprzedniego stanu i spróbujemy następnej wartości. Jeśli żadna wartość nie działa, zwracamy niepowodzenie. Część drzewa wyszukiwania problemu Australii jest pokazana na rysunku , gdzie przypisaliśmy zmienne w kolejności WA, NT, Q …
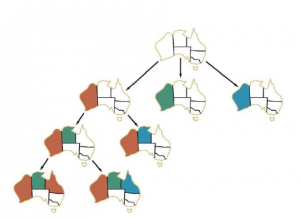
Zauważ, że BACKTRACKING-SEARCH zachowuje tylko jedną reprezentację stanu (przypisania) i zmienia tę reprezentację zamiast tworzyć nowe.
Podczas gdy algorytmy wyszukiwania bez informacji można ulepszyć tylko poprzez dostarczenie im heurystyk specyficznych dla domeny, okazuje się, że wyszukiwanie z nawrotem można ulepszyć za pomocą heurystyk niezależnych od domeny, które wykorzystują czynnikową reprezentację CSP. Pokazujemy, jak to się robi.