Popularna łamigłówka Sudoku wprowadziła miliony ludzi w problemy z ograniczaniem satysfakcji, chociaż mogą nie zdawać sobie z tego sprawy. Plansza Sudoku składa się z 81 kwadratów, z których niektóre są początkowo wypełnione cyframi od 1 do 9. Układanka polega na wypełnieniu wszystkich pozostałych kwadratów tak, aby żadna cyfra nie pojawiła się dwa razy w każdym rzędzie, kolumnie lub polu 3 x 3 . Wiersz, kolumna lub pole nazywa się jednostką.
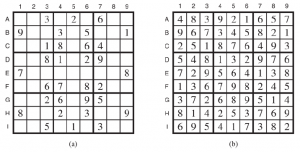
Zagadki Sudoku, które pojawiają się w gazetach i książkach z puzzlami, mają tę właściwość, że istnieje dokładnie jedno rozwiązanie. Chociaż niektóre z nich mogą być trudne do rozwiązania ręcznego, co zajmuje dziesiątki minut, solver CSP może obsłużyć tysiące zagadek na sekundę. Łamigłówkę Sudoku można uznać za CSP z 81 zmiennymi, po jednej dla każdego kwadratu. Używamy nazw zmiennych od A1 do A9 dla górnego rzędu (od lewej do prawej), do I1 do I9 dla dolnego rzędu. Puste kwadraty mają domenę {1,2,3,4,5,6,7,8,9}, a kwadraty wstępnie wypełnione mają domenę składającą się z jednej wartości. Ponadto istnieje 27 różnych ograniczeń Alldiff, po jednym dla każdej jednostki (rzędu, kolumny i pola 9 kwadratów):

Zobaczmy, jak daleko może nas zaprowadzić spójność łuku. Załóżmy, że ograniczenia Alldiff zostały rozszerzone na ograniczenia binarne (takie jak A1 ≠ A2 ), dzięki czemu możemy zastosować AC-3 algorytm bezpośrednio. Rozważ zmienną E6 – pusty kwadrat między 2 i 8 w środkowym polu. Z ograniczeń w pudełku możemy usunąć 1, 2, 7 i 8 z domeny E6. Z ograniczeń w jego kolumnie możemy wyeliminować 5, 6, 2, 8, 9 i 3 (chociaż 2 i 8 zostały już usunięte). To pozostawia E6 z domeną {4} ; innymi słowy, znamy odpowiedź na E6. Rozważmy teraz zmienną I6 – kwadrat w dolnym środkowym polu otoczony przez 1, 3 i 3. Stosując spójność łuku w jego kolumnie, eliminujemy 5, 6, 2, 4 (odkąd wiemy, że E6 musi wynosić 4), 8, 9 i 3. Eliminujemy 1 przez spójność łukową z I5, a zostaje nam tylko wartość 7 w dziedzinie I6. Teraz w kolumnie 6 jest 8 znanych wartości, więc spójność łuku może wywnioskować, że A6 musi wynosić 1. Wnioskowanie jest kontynuowane wzdłuż tych linii i ostatecznie AC-3 może rozwiązać całą zagadkę – wszystkie zmienne mają swoje domeny zredukowane do jednej wartości.
Oczywiście Sudoku wkrótce straciłoby swoją atrakcyjność, gdyby każdą łamigłówkę można było rozwiązać mechanicznie za pomocą AC-3, a AC-3 działa tylko w przypadku najłatwiejszych łamigłówek Sudoku. Nieco trudniejsze można rozwiązać za pomocą PC-2, ale przy większych kosztach obliczeniowych: w łamigłówce Sudoku jest 255 960 różnych ograniczeń ścieżki. Aby rozwiązać najtrudniejsze zagadki i poczynić skuteczne postępy, będziemy musieli być sprytniejsi. Rzeczywiście, atrakcyjność łamigłówek Sudoku dla człowieka rozwiązującego polega na potrzebie zaradności w stosowaniu bardziej złożonych strategii wnioskowania. Miłośnicy nadają im barwne nazwy, takie jak „nagie trójki”. Ta strategia działa w następujący sposób: w dowolnej jednostce (wierszu, kolumnie lub polu) znajdź trzy kwadraty, z których każdy ma domenę zawierającą te same trzy liczby lub podzbiór tych liczb. Na przykład trzy domeny mogą być {1,8}, {3,8} , {1,3,8} . Z tego nie wiemy, który kwadrat zawiera 1, 3 lub 8, ale wiemy, że te trzy liczby muszą być rozdzielone między trzy kwadraty. Dlatego możemy usunąć 1, 3 i 8 z domen co drugiego kwadratu w jednostce. Warto zauważyć, jak daleko możemy się posunąć, nie mówiąc zbyt wiele o tym, co jest specyficzne dla Sudoku. Musimy oczywiście powiedzieć, że istnieje 81 zmiennych, ich domenami są cyfry od 1 do 9 i że istnieje 27 ograniczeń Alldiff. Ale poza tym wszystkie strategie – spójność łuku, spójność ścieżki itd. — mają zastosowanie ogólnie do wszystkich dostawców CSP, a nie tylko do problemów Sudoku. Nawet nagie trójki są tak naprawdę strategią wymuszania spójności ograniczeń i nie są specyficzne dla Sudoku per se. Na tym polega siła formalizmu CSP: dla każdego nowego obszaru problemowego wystarczy zdefiniować problem w kategoriach ograniczeń; wtedy ogólne mechanizmy rozwiązywania ograniczeń mogą przejąć kontrolę.