Zasady Kriegspiel są następujące: każdy biały i czarny widzą planszę zawierającą tylko własne pionki. Sędzia, który widzi wszystkie figury, rozstrzyga mecz i okresowo wydaje komunikaty, które są słyszane przez obu graczy. Po pierwsze, biały proponuje sędziemu posunięcie, które byłoby legalne, gdyby nie było czarnych figur. Jeśli czarne bierki zapobiegną ruchowi, sędzia ogłasza „nielegalne”, a białe proponują ruchy, dopóki nie zostanie znaleziony legalny – dowiadują się więcej o lokalizacji bierek czarnych w tym procesie. Po zaproponowaniu legalnego posunięcia sędzia ogłasza jedną lub więcej z następujących czynności:
„Bicie na polu X”, jeśli doszło do bicia, i „Szach przez D”, jeśli czarny król jest szachowany, gdzie D jest kierunkiem szachu i może być jednym z „skoczek”, „rangi”, „pliku”. ”, „Długa przekątna” lub „Krótka przekątna”. Jeżeli czarne są zamatowane lub patowe, sędzia o tym mówi; w przeciwnym razie kolej na ruch czarnych. Kriegspiel może wydawać się przerażająco niemożliwy, ale ludzie radzą sobie z nim całkiem dobrze i programy komputerowe zaczynają nadrabiać zaległości. Pomaga przywołać pojęcie stanu przekonań – zbiór wszystkich logicznie możliwych stanów tablicy, biorąc pod uwagę pełną historię dotychczasowych percepcji. Początkowo stan wiary białych jest singletonem, ponieważ pionki czarnych jeszcze się nie poruszyły. Po tym, jak biały wykona ruch i czarny odpowie, stan wiary białych zawiera 20 pozycji, ponieważ czarny ma 20 odpowiedzi na każdy ruch otwierający. Śledzenie stanu przekonania w miarę postępu gry jest właśnie problemem estymacji stanu, dla którego krok aktualizacji jest podany w równaniu. Możemy mapować estymację stanu Kriegspiela bezpośrednio na częściowo obserwowalne, niedeterministyczne ramy sekcji, jeśli uważamy przeciwnika za źródło niedeterminizmu; to znaczy, WYNIKI ruchu białych składają się z (przewidywalnego) wyniku własnego ruchu białych i nieprzewidywalnego wyniku podanego przez odpowiedź czarnych. Biorąc pod uwagę obecny stan przekonań, biały może zapytać: „Czy mogę wygrać grę?” W przypadku częściowo obserwowalnej gry zmienia się pojęcie strategii; zamiast określać ruch dla każdego możliwego ruchu, który może wykonać przeciwnik, potrzebujemy ruchu dla każdej możliwej sekwencji perceptu, która może zostać odebrana. Dla Kriegspiel strategia wygrywająca lub gwarantowany mat to taka, która dla każdej możliwej sekwencji percepcji prowadzi do rzeczywistego mata dla każdego możliwego stanu szachownicy w obecnym stanie przekonania, niezależnie od tego, jak porusza się przeciwnik. Przy tej definicji stan wiary przeciwnika jest nieistotny – strategia musi działać, nawet jeśli przeciwnik widzi wszystkie pionki. To znacznie upraszcza obliczenia. Rysunek pokazuje część gwarantowanego mata w końcówce KRK (król i wieża kontra król).
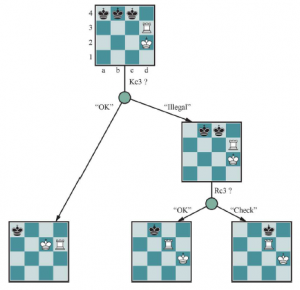
W tym przypadku czarny ma tylko jedną figurę (króla), więc stan wiary białych można pokazać na pojedynczej planszy, zaznaczając każdą możliwą pozycję czarnego króla.
Ogólny algorytm wyszukiwania AND-OR może być zastosowany do przestrzeni stanów przekonań w celu znalezienia gwarantowanych matów. Przyrostowy algorytm stanu przekonania, często znajduje matów w środkowej fazie gry do głębokości 9 – znacznie powyżej umiejętności większości ludzkich graczy. Oprócz gwarantowanych matów Kriegspiel dopuszcza zupełnie nową koncepcję, która nie ma sensu w grach w pełni obserwowalnych: mat probabilistyczny. Take maty nadal muszą pracować w każdym stanie szachownicy w stanie wiary; są probabilistyczne w odniesieniu do losowości ruchów zwycięskiego gracza. Aby uzyskać podstawową ideę, rozważ problem znalezienia samotnego czarnego króla przy użyciu tylko białego króla. Po prostu poruszając się losowo, biały król w końcu wpadnie na czarnego króla, nawet jeśli ten spróbuje uniknąć tego losu, ponieważ czarne nie mogą w nieskończoność odgadywać właściwych ruchów unikowych. W terminologii teorii prawdopodobieństwa wykrycie występuje z prawdopodobieństwem 1. Koniec gry KBNK – król, goniec i skoczek kontra król – wygrywa w tym sensie; Biały przedstawia czarnemu nieskończoną losową sekwencję wyborów, z których jeden czarny odgadnie błędnie i ujawni swoją pozycję, prowadząc do mata. Z drugiej strony końcówka KBBK wygrywa z prawdopodobieństwem 1-e . Białe mogą wymusić zwycięstwo tylko poprzez pozostawienie jednego ze swoich gońców bez ochrony na jeden ruch. Jeśli czarny znajdzie się we właściwym miejscu i zbije gońca (posunięcie, które byłoby nielegalne, gdyby gońce były chronione), gra jest remisowana. Białe mogą zdecydować się na wykonanie ryzykownego ruchu w jakimś losowo wybranym punkcie w środku bardzo długiej sekwencji, redukując w ten sposób do dowolnie małej stałej, ale nie mogą zredukować do zera. Czasami strategia mata działa dla niektórych stanów szachownicy w obecnym stanie przekonań, ale nie dla innych. Próba takiej strategii może się udać, prowadząc do przypadkowego mata – przypadkowego w tym sensie, że białe nie mogą wiedzieć, że będzie to mat – jeśli bierki czarnych znajdą się we właściwych miejscach. (Większość matów w grach między ludźmi ma tę przypadkową naturę.) Pomysł ten w naturalny sposób prowadzi do pytania, jak prawdopodobne jest, że dana strategia wygra, co z kolei prowadzi do pytania, na ile prawdopodobne jest, że każda plansza obecny stan przekonań to prawdziwy stan planszy. Na pierwszy rzut oka można by zasugerować, że wszystkie stany tablicy w obecnym stanie przekonań są jednakowo prawdopodobne — ale to nie może być właściwe. Rozważmy na przykład stan wiary białych po pierwszym ruchu czarnych w grze. Z definicji (zakładając, że czarny gra optymalnie), czarny musiał zagrać optymalny ruch, więc wszystkim stanom planszy wynikającym z suboptymalnych ruchów należy przypisać prawdopodobieństwo zerowe.
Ten argument też nie jest do końca słuszny, ponieważ celem każdego gracza jest nie tylko przeniesienie pionków na odpowiednie pola, ale także zminimalizowanie informacji, jakie ma przeciwnik na temat ich lokalizacji. Granie jakąkolwiek przewidywalną „optymalną” strategią dostarcza przeciwnikowi informacji. W związku z tym optymalna gra w częściowo obserwowalnych grach wymaga chęci grania nieco losowo. (Dlatego inspektorzy higieny restauracji przeprowadzają wyrywkowe wizyty kontrolne.) To oznacza okazjonalne wybieranie ruchów, które mogą wydawać się „wewnętrznie” słabe, ale zyskują na sile dzięki swojej nieprzewidywalności, ponieważ przeciwnik prawdopodobnie nie przygotował przed nimi żadnej obrony.
Z tych rozważań wydaje się, że prawdopodobieństwa związane ze stanami tablicy w obecnym stanie przekonań można obliczyć tylko przy optymalnej strategii randomizowanej; z kolei obliczenie tej strategii wydaje się wymagać znajomości prawdopodobieństw różnych stanów, w których może znajdować się plansza. Ta zagadka może zostać rozwiązana przez przyjęcie teorii gry dotyczącej rozwiązania równowagi, o czym będziemy mówić dalej w rozdziale 17 . Równowaga określa optymalną strategię losową dla każdego gracza. Obliczanie równowagi jest zbyt kosztowne dla Kriegspiela. Obecnie projektowanie efektywnych algorytmów dla ogólnej gry Kriegspiel jest otwartym tematem badawczym. Większość systemów przeprowadza przewidywanie o ograniczonej głębokości we własnej przestrzeni stanów przekonań, ignorując stan przekonań przeciwnika. Funkcje ewaluacyjne przypominają te z obserwowalnej gry, ale zawierają składnik określający wielkość stanu przekonań – mniejsze jest lepsze! Powrócimy do gier częściowo obserwowalnych pod tematem teorii gier