Miesiąc: wrzesień 2021

Problem wyszukiwania online jest rozwiązywany przez przeplatanie obliczeń, wykrywania i działania. Zaczniemy od założenia deterministycznego i w pełni obserwowalnego środowiska (rozdział 17 rozluźnia te założenia) i zastrzeżemy, że agent wie tylko:

* DZIAŁANIA, czynności prawne w stanie;

* c(s,a,s’) , koszt zastosowania akcji w stanie s, aby dojść s’ do stanu . Zauważ, że nie można tego użyć, dopóki agent nie wie, że wynikiem jest s’.

* Is-GOAL(s), test celu.

W szczególności należy zauważyć, że agent nie może określić WYNIKU(ów, a) z wyjątkiem faktycznego przebywania i wykonywania . Na przykład w problemie labiryntu pokazanym na rysunku , agent nie wie, że przejście w górę z (1,1) prowadzi do (1,2); ani po zrobieniu tego nie wie, że zejście w dół spowoduje powrót do (1,1). Ten stopień ignorancji można zmniejszyć w niektórych zastosowaniach – na przykład eksplorator robota może wiedzieć, jak działają jego ruchy i nie znać tylko lokalizacji przeszkód.

Wreszcie agent może mieć dostęp do dopuszczalnej funkcji heurystycznej h(s), która szacuje odległość od stanu bieżącego do stanu docelowego. Na przykład na rysunku powyżej agent może znać lokalizację celu i być w stanie użyć heurystyki odległości Manhattan . Zazwyczaj celem agenta jest osiągnięcie stanu docelowego przy minimalizacji kosztów. (Innym możliwym celem jest po prostu zbadanie całego środowiska). Koszt to całkowity koszt ścieżki, który agent ponosi podczas podróży. Często porównuje się ten koszt z kosztem ścieżki, jaki poniósłby agent, gdyby znał z góry przestrzeń wyszukiwania — to znaczy optymalną ścieżkę w znanym środowisku. W języku algorytmów internetowych porównanie to nazywa się współczynnikiem konkurencyjności; chcielibyśmy, aby był jak najmniejszy. Odkrywcy online są narażeni na ślepe zaułki: stany, z których żaden stan docelowy nie jest osiągalny. Jeśli agent nie wie, co robi każda akcja, może wykonać akcję „skoku w bezdenną otchłań”, a tym samym nigdy nie osiągnąć celu. Ogólnie rzecz biorąc, żaden algorytm nie może uniknąć ślepych zaułków we wszystkich przestrzeniach stanów. Rozważmy dwie martwe przestrzenie stanów na rysunku (a) . Algorytm wyszukiwania online, który odwiedził stany A i S, nie może stwierdzić, czy jest w stanie górnym, czy dolnym; oba wyglądają identycznie w zależności od tego, co widział agent. Dlatego nie może wiedzieć, jak wybrać właściwą akcję w obu przestrzeniach stanów. Jest to przykład argumentu adwersarza — możemy sobie wyobrazić przeciwnika konstruującego przestrzeń stanów, podczas gdy agent ją bada i umieszcza cele i ślepe zaułki, gdziekolwiek chce, jak na rysunku (b).

Ślepe zaułki są prawdziwym utrudnieniem dla eksploracji robotów – klatki schodowe, rampy, klify, ulice jednokierunkowe, a nawet naturalny teren – wszystkie obecne stany, z których niektóre działania są nieodwracalne – nie ma możliwości powrotu do poprzedniego stanu. Algorytm eksploracji, który przedstawimy, gwarantuje działanie tylko w przestrzeniach stanów, które można bezpiecznie eksplorować — to znaczy, że pewien stan docelowy jest osiągalny z każdego stanu osiągalnego. Przestrzenie stanów, w których występują tylko akcje odwracalne, takie jak labirynty i 8 zagadek, są wyraźnie bezpiecznie eksplorowane (jeśli w ogóle mają jakieś rozwiązanie). Temat bezpiecznej eksploracji omówimy bardziej szczegółowo w sekcji 22.3.2. Nawet w środowiskach, w których można bezpiecznie eksplorować, nie można zagwarantować żadnego ograniczonego współczynnika konkurencyjności, jeśli istnieją ścieżki o nieograniczonych kosztach. Łatwo to pokazać w środowiskach z nieodwracalnymi działaniami, ale w rzeczywistości pozostaje to również prawdziwe w przypadku odwracalnym, jak pokazuje Rysunek 4.20(b). Z tego powodu często charakteryzuje się wydajność algorytmów wyszukiwania online pod kątem rozmiaru całej przestrzeni stanów, a nie tylko głębokości najpłytszego celu.

Do tej pory koncentrowaliśmy się na agentach korzystających z algorytmów wyszukiwania offline. Obliczają kompletne rozwiązanie przed podjęciem pierwszego działania. W przeciwieństwie do tego, internetowy agent wyszukiwania przeplata obliczenia i działanie: najpierw wykonuje działanie, następnie obserwuje środowisko i oblicza następne działanie. Wyszukiwanie online jest dobrym pomysłem w środowiskach dynamicznych lub półdynamicznych, gdzie kara za zbyt długie siedzenie i korzystanie z komputera. Wyszukiwanie online jest również pomocne w domenach niedeterministycznych, ponieważ pozwala agentowi skoncentrować swoje wysiłki obliczeniowe na zdarzeniach, które faktycznie się pojawiają, a nie na tych, które mogą się zdarzyć, ale prawdopodobnie nie nastąpią. Oczywiście jest kompromis: im więcej agent planuje z wyprzedzeniem, tym rzadziej znajdzie się w strumieniu bez wiosła. W nieznanych środowiskach, w których agent nie wie, jakie stany istnieją ani co robią jego działania, agent musi wykorzystać swoje działania jako eksperymenty, aby poznać środowisko. Kanonicznym przykładem wyszukiwania online jest problem z mapowaniem: robot jest umieszczany w nieznanym budynku i musi zbadać, aby zbudować mapę, która może być później wykorzystana do dostania się z do . Metody ucieczki z labiryntów – wiedza wymagana dla aspirujących bohaterów starożytności – to także przykłady algorytmów wyszukiwania w sieci. Eksploracja przestrzenna nie jest jednak jedyną formą eksploracji online. Rozważmy noworodka: ma wiele możliwych działań, ale nie zna skutków żadnego z nich i doświadczyło tylko kilku możliwych stanów, które może osiągnąć.

Agent dla środowisk częściowo obserwowalnych formułuje problem, wywołuje algorytm wyszukiwania (taki jak AND-LUB-SEARCH) w celu jego rozwiązania i wykonuje rozwiązanie. Istnieją dwie główne różnice między tym agentem a tym dla w pełni obserwowalnych środowisk deterministycznych. Po pierwsze, rozwiązaniem będzie plan warunkowy, a nie sekwencja; aby wykonać wyrażenie if-then-else, agent będzie musiał przetestować warunek i wykonać odpowiednią gałąź warunku. Po drugie, agent będzie musiał utrzymać swój stan wiary podczas wykonywania działań i odbierania percepcji. Proces ten przypomina proces przewidywania-obserwacji-aktualizacji w równaniu ), ale w rzeczywistości jest prostszy, ponieważ percepcja jest przekazywana przez środowisko, a nie obliczana przez agenta. Biorąc pod uwagę początkowy stan przekonań , działanie i percepcję , nowy stan przekonań to:

Rozważmy przedszkolny świat próżni, w którym agenci wyczuwają tylko stan swojego obecnego placu, a każdy plac może się zabrudzić w dowolnym momencie, chyba że agent aktywnie go czyści w danym momencie. Rysunek przedstawia stan przekonania utrzymywany w tym środowisku.

W środowiskach częściowo obserwowalnych – które obejmują zdecydowaną większość środowisk świata rzeczywistego – utrzymywanie własnego stanu wiary jest podstawową funkcją każdego inteligentnego systemu. Ta funkcja nosi różne nazwy, w tym monitorowanie, filtrowanie i estymację stanu. Równanie powyższe nazywa się rekurencyjnym estymatorem stanu, ponieważ oblicza nowy stan przekonania z poprzedniego, a nie przez badanie całej sekwencji percepcji. Jeśli agent nie ma „zostać w tyle”, obliczenia muszą odbywać się tak szybko, jak pojawiają się spostrzeżenia. Gdy środowisko staje się bardziej złożone, agent będzie miał tylko czas na obliczenie przybliżonego stanu przekonań, być może skupiając się na implikacjach postrzeganie aspektów środowiska będących przedmiotem bieżącego zainteresowania. Większość prac nad tym problemem została wykonana dla stochastycznych środowisk o stanie ciągłym za pomocą narzędzi teorii prawdopodobieństwa

W częściowo obserwowalnych środowiskach — które obejmują zdecydowaną większość rzeczywistych środowisk — utrzymywanie własnego stanu wiary jest podstawową funkcją każdego inteligentnego systemu. Ta funkcja nosi różne nazwy, w tym monitorowanie, filtrowanie i estymację stanu. Równanie powyższe jest nazywane rekurencyjnym estymatorem stanu, ponieważ oblicza nowy stan przekonania z poprzedniego, a nie przez badanie całej sekwencji percepcji. Jeśli agent nie ma „zostać w tyle”, obliczenia muszą odbywać się tak szybko, jak pojawiają się spostrzeżenia. Gdy środowisko staje się bardziej złożone, agent będzie miał tylko czas na obliczenie przybliżonego stanu przekonań, być może skupiając się na implikacjach postrzeganie aspektów środowiska będących przedmiotem aktualnego zainteresowania. Większość prac nad tym problemem została wykonana dla stochastycznych środowisk o stanie ciągłym za pomocą narzędzi teorii prawdopodobieństwa. W tej sekcji pokażemy przykład w dyskretnym środowisku z czujnikami deterministycznymi i działaniami niedeterministycznymi. Przykład dotyczy robota z konkretnym zadaniem oceny stanu zwanym lokalizacją: ustaleniem, gdzie się znajduje, mając do dyspozycji mapę świata oraz sekwencję percepcji i działań. Nasz robot znajduje się w podobnym do labiryntu środowisku z rysunku 4.18. Robot jest wyposażony w cztery czujniki sonaru, które informują, czy w każdym z czterech kierunków kompasu znajduje się przeszkoda — zewnętrzna ściana czy ciemny kwadrat na figurze. Percept ma postać wektora bitowego, po jednym bitu dla każdego kierunku północ, wschód, południe i zachód w tej kolejności, więc 1011 oznacza, że ​​istnieją przeszkody na północy, południu i zachodzie, ale nie na wschodzie.

Zakładamy, że czujniki podają idealnie poprawne dane, a robot ma poprawną mapę otoczenia. Niestety, system nawigacyjny robota jest zepsuty, więc wykonując akcję Właściwą, porusza się on losowo na jedno z sąsiednich pól. Zadaniem robota jest określenie jego aktualnej lokalizacji. Załóżmy, że robot został właśnie włączony i nie wie, gdzie jest – jego inicjał to stan przekonania składa się ze zbioru wszystkich lokalizacji. Następnie robot odbiera percept 1011 i dokonuje aktualizacji przy użyciu równania b0 = UPDATE(1011) , dając 4 lokalizacje pokazane na rysunku 4.18(a) . Możesz zbadać labirynt, aby zobaczyć, że są to jedyne cztery lokalizacje, które dają percepcję 1011. Następnie robot wykonuje akcję Właściwą, ale wynik jest niedeterministyczny. Nowy stan przekonania, ba = PREDICT(b0,RIGHT) , zawiera wszystkie lokalizacje, które są o jeden krok od lokalizacji w . Kiedy pojawia się drugi percept, 1010, robot wykonuje UPDATE(1010) i stwierdza, że ​​stan przekonania zapadł się do pojedynczej lokalizacji pokazanej na rysunku 4.18(b). To jedyna lokalizacja, która może być wynikiem

W przypadku działań niedeterministycznych krok PREDICT zwiększa stan przekonania, ale krok UPDATE zmniejsza go z powrotem, o ile spostrzeżenia dostarczają użytecznych informacji identyfikacyjnych. Czasami percepcje nie pomagają zbytnio w lokalizacji: gdyby istniał jeden lub więcej długich korytarzy wschód-zachód, robot mógłby otrzymać długą sekwencję 1010 percepcji, ale nigdy nie wiedział, gdzie w korytarzu (korytarzach) się znajdował. Jednak w środowiskach o rozsądnej zmienności geograficznej lokalizacja często szybko zbliża się do jednego punktu, nawet jeśli działania nie są deterministyczne. Co się stanie, jeśli czujniki są uszkodzone? Jeśli możemy rozumować tylko za pomocą logiki Boole’a, to musimy traktować każdy bit czujnika jako poprawny lub niepoprawny, co jest równoznaczne z brakiem jakichkolwiek informacji percepcyjnych. Zobaczymy jednak, że rozumowanie probabilistyczne (rozdział 12) pozwala nam wydobyć użyteczne informacje z wadliwego czujnika, o ile jest on błędny przez mniej niż połowę czasu.

Poprzednia sekcja pokazała, jak wyprowadzić funkcję WYNIKÓW dla niedeterministycznego problemu stanu przekonań z ukrytego problemu fizycznego, biorąc pod uwagę funkcję PERCEPT. Dzięki temu sformułowaniu algorytm wyszukiwania AND–OR może być zastosowany bezpośrednio do uzyskania rozwiązania. Rysunek poniżej przedstawia część drzewa poszukiwań świata próżni z wykrywaniem lokalnym, przy założeniu początkowej percepcji [A,Dirty]. Rozwiązaniem jest plan warunkowy

Zauważ, że ponieważ dostarczyliśmy problem stanu przekonań do algorytmu wyszukiwania AND-OR, zwrócił on plan warunkowy, który testuje stan przekonań, a nie stan faktyczny. Tak właśnie powinno być: w częściowo obserwowalnym środowisku agent nie będzie znał faktycznego stanu. Podobnie jak w przypadku standardowych algorytmów wyszukiwania stosowanych do problemów bezczujnikowych, algorytm wyszukiwania AND–OR traktuje stany przekonań jako czarne skrzynki, tak jak wszystkie inne stany. Można to poprawić, sprawdzając wcześniej wygenerowane stany przekonań, które są podzbiorami lub nadzbiorami obecnego stanu, podobnie jak w przypadku problemów bezczujnikowych. Można również wyprowadzić przyrostowe algorytmy wyszukiwania, analogiczne do tych opisanych dla problemów bezczujnikowych, które zapewniają znaczne przyspieszenie w porównaniu z podejściem czarnej skrzynki.

Wielu problemów nie da się rozwiązać bez wykrywania. Na przykład bezczujnikowa 8-łamigłówka jest niemożliwa. Z drugiej strony, odrobina wyczuwania może zajść daleko: możemy rozwiązać 8-zagadek, jeśli widzimy tylko kwadrat w lewym górnym rogu. Rozwiązanie polega na przenoszeniu każdego kafelka po kolei na obserwowalny kwadrat i od tego momentu śledzeniu jego lokalizacji. W przypadku częściowo obserwowalnego problemu, specyfikacja problemu będzie określać funkcję Percept(s), która zwraca percept odebrany przez agenta w danym stanie. Jeśli wykrywanie jest niedeterministyczne, możemy użyć funkcji PERCEPTS, która zwraca zestaw możliwych perceptów. Dla problemów w pełni obserwowalnych Percept(s) = s lub każdy stan , a dla problemów bezczujnikowych percept(s) = null. Rozważmy świat próżni z wykrywaniem lokalnym, w którym agent ma czujnik położenia, który daje wynik L w lewym kwadracie i R w prawym kwadracie, oraz czujnik zanieczyszczenia, który pokazuje Brudny, gdy bieżący kwadrat jest brudny i Czysty, gdy jest brudny. to czyste. Zatem PERCEPT w stanie 1 to [L,Dirty]. Przy częściowej obserwowalności zwykle będzie tak, że kilka stanów wytwarza to samo postrzeganie; stan 3 również wygeneruje [L,Dirty]. Zatem, biorąc pod uwagę to początkowe spostrzeżenie, początkowy stan przekonań będzie {1,3} . Możemy myśleć, że model przejścia między stanami przekonań dla częściowo obserwowalnych problemów występuje w trzech etapach, jak pokazano na rysunku:

* Etap przewidywania oblicza stan przekonania wynikający z działania, RESULT(b,a) , dokładnie tak samo jak w przypadku problemów bezczujnikowych. Aby podkreślić, że jest to przewidywanie, używamy notacji

gdzie „kapelusz” oznacza „szacowany”, a także używamy PREDICT(b,a) jako synonimu RESULT(b,a).

* Etap możliwych percepcji oblicza zbiór percepcji, które można zaobserwować w przewidywanym stanie przekonań (używając litery do obserwacji):

* Etap aktualizacji oblicza, dla każdego możliwego spostrzeżenia, stan przekonania, który wynikałby z tego spostrzeżenia. Zaktualizowany stan przekonania b₀ jest zbiorem stanów, w których mógł powstać percepcja

Agent musi poradzić sobie z możliwymi spostrzeżeniami w czasie planowania, ponieważ nie będzie znał rzeczywistych percepcji, dopóki nie wykona planu. Zauważ, że niedeterminizm w środowisku fizycznym może powiększyć stan przekonania na etapie przewidywania, ale każdy zaktualizowany stan przekonania b₀ nie może być większy niż przewidywany stan przekonania ; obserwacje mogą jedynie pomóc w zmniejszeniu niepewności. Co więcej, w przypadku odczuwania deterministycznego stany przekonań dla różnych możliwych percepcji będą rozłączne, tworząc podział pierwotnego przewidywanego stanu przekonań. Łącząc te trzy etapy, otrzymujemy możliwe stany przekonań wynikające z danego działania oraz kolejne możliwe spostrzeżenia:

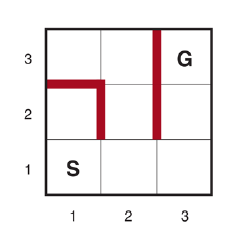
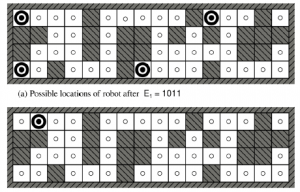
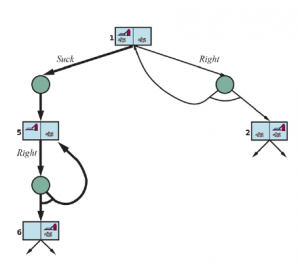
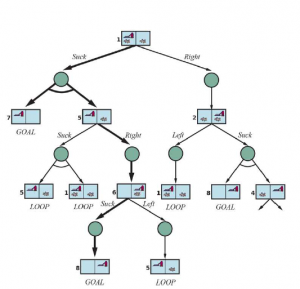
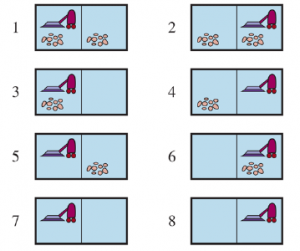
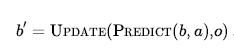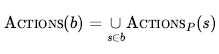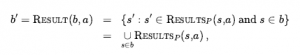Kiedy percepcje agenta nie dostarczają żadnych informacji, mamy coś, co nazywamy problemem bezczujnikowym (lub problemem zgodnym). Na początku możesz pomyśleć, że agent bezczujnikowy nie ma nadziei na rozwiązanie problemu, jeśli nie ma pojęcia, w jakim stanie zaczyna, ale rozwiązania bezczujnikowe są zaskakująco powszechne i przydatne, głównie dlatego, że nie opierają się na prawidłowym działaniu czujników. Na przykład w systemach produkcyjnych opracowano wiele pomysłowych metod prawidłowego orientowania części z nieznanej pozycji początkowej za pomocą sekwencji działań bez żadnego wykrywania. Czasami plan bezczujnikowy jest lepszy, nawet jeśli dostępny jest plan warunkowy z wykrywaniem. Na przykład lekarze często przepisują antybiotyk o szerokim spektrum działania, zamiast stosować warunkowy plan wykonania badania krwi, a następnie czekania na powrót wyników, a następnie przepisywania bardziej specyficznego antybiotyku. Plan bezczujnikowy oszczędza czas i pieniądze oraz zapobiega ryzyku pogorszenia infekcji przed udostępnieniem wyników testu. Rozważmy bezczujnikową wersję (deterministycznego) świata próżni. Załóż, że agent zna geografię swojego świata, ale nie zna własnego położenia czy rozmieszczenia brudu. W takim przypadku początkowy stan przekonania to {1,2,3,4,5,6,7,8} (patrz Rysunek 4.9 ). Teraz, jeśli agent poruszy się w prawo, będzie w jednym ze stanów {2,4,6,8} — agent uzyskał informacje, nie dostrzegając czegokolwiek! Po [Right,Suck] agent zawsze znajdzie się w jednym ze stanów {4,8}. Wreszcie, po [Right,Suck,Left,Suck] agent ma zagwarantowane osiągnięcie stanu docelowego 7, bez względu na stan początkowy. Mówimy, że agent może zmusić świat do stanu 7.

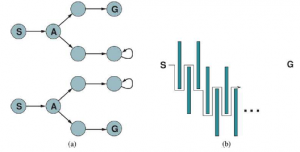
Rozwiązaniem problemu bezczujnikowego jest sekwencja działań, a nie plan warunkowy (bo nie ma percepcji). Ale szukamy raczej w przestrzeni stanów przekonań niż stanów fizycznych. W przestrzeni stanów przekonań problem jest w pełni obserwowalny, ponieważ podmiot zawsze zna swój stan przekonań. Co więcej, rozwiązaniem (jeśli istnieje) problemu bezczujnikowego jest zawsze sekwencja działań. Dzieje się tak, ponieważ, jak w zwykłych problemach z rozdziału 3, percepcje otrzymywane po każdym działaniu są całkowicie przewidywalne — zawsze są puste! Nie ma więc żadnych nieprzewidzianych okoliczności do planowania. Dzieje się tak, nawet jeśli środowisko jest niedeterministyczne. Moglibyśmy wprowadzić nowe algorytmy rozwiązywania problemów wyszukiwania bezczujnikowego. Ale zamiast tego możemy użyć istniejącego algorytmy, jeśli przekształcimy leżący u jego podstaw problem fizyczny w problem stanu przekonań, w którym poszukujemy raczej stanów przekonań niż stanów fizycznych. Pierwotny problem P ma komponenty Actions_P, Result_P itd., a problem stanu przekonań składa się z następujących komponentów:

* STATES: Przestrzeń stanów przekonań zawiera każdy możliwy podzbiór stanów fizycznych. Jeśli P ma N stanów, to problem stanów przekonań ma 2^N stanów przekonań, chociaż wiele z nich może być nieosiągalnych ze stanu początkowego.

* INITIAL STATE: Zazwyczaj stan przekonań składający się ze wszystkich stanów w P , chociaż w niektórych przypadkach agent będzie miał więcej wiedzy niż ta.

* ACTIONS: Jest to nieco trudne. Załóżmy, że agent jest w stanie przekonania b = {s₁,s₂}, ale 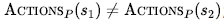wtedy agent nie jest pewien, które działania są legalne. Jeśli założymy, że nielegalne działania nie mają wpływu na środowisko, można bezpiecznie połączyć wszystkie działania w dowolnym stanie fizycznym w obecnym stanie przekonań b:

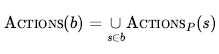
Z drugiej strony, jeśli nielegalne działanie może prowadzić do katastrofy, bezpieczniej jest dopuścić tylko skrzyżowanie, czyli zestaw działań legalnych we wszystkich stanach. W świecie próżni każde państwo ma takie same działania prawne, więc obie metody dają ten sam wynik.

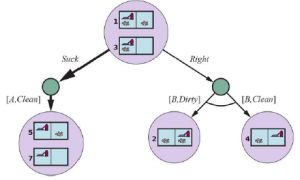
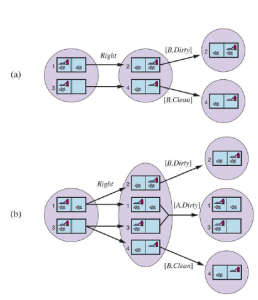
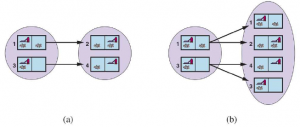
  * TRANSITION MODEL: W przypadku działań deterministycznych nowy stan przekonań ma jeden stan wynikowy dla każdego z obecnych możliwych stanów (chociaż niektóre stany wynikowe mogą być takie same):

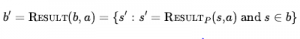
W przypadku niedeterminizmu nowy stan przekonań składa się ze wszystkich możliwych wyników zastosowania działania do dowolnego ze stanów obecnego stanu przekonań:

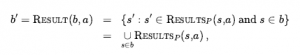
Rozmiar b’ będzie taki sam lub mniejszy niż w przypadku działań deterministycznych, ale może być większy niż w przypadku działań niedeterministycznych

* GOAL TEST: Agent prawdopodobnie osiąga cel, jeśli jakikolwiek stan w stanie przekonań spełnia test celu leżącego u podstaw problemu, IS-GOAL_P(s) . Agent koniecznie osiąga cel, jeśli każdy stan spełnia IS-_GOALP(s). Naszym celem jest koniecznie osiągnięcie celu.

* ACTION COST: To też jest trudne. Jeśli to samo działanie może mieć różne koszty w różnych stanach, to koszt podjęcia działania w danym stanie przekonań może być jedną z kilku wartości. Na razie zakładamy, że koszt działania jest taki sam we wszystkich stanach, a więc może być przeniesiony bezpośrednio z podstawowego problemu fizycznego.

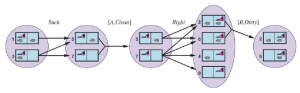
Rysunek przedstawia osiągalną przestrzeń stanów przekonań dla deterministycznego, bezczujnikowego świata próżni. Jest tylko 12 osiągalnych stanów przekonań spośród 2⁸ = 256 możliwych stanów przekonań.

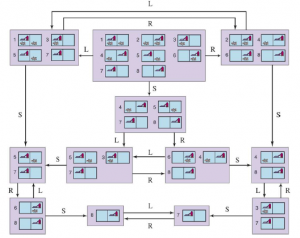
Powyższe definicje umożliwiają automatyczne skonstruowanie sformułowania problemu stanu przekonań na podstawie definicji leżącego u jego podstaw problemu fizycznego. Gdy to zrobimy, możemy rozwiązać problemy bezczujnikowe za pomocą dowolnego zwykłego algorytmu wyszukiwania z rozdziału 3 . W zwykłym przeszukiwaniu wykresów nowo osiągnięte stany są testowane, aby sprawdzić, czy zostały wcześniej osiągnięte. Działa to również w przypadku stanów przekonań; na przykład na rysunku sekwencja działań [Ssanie,Lewo,Ssanie] rozpoczynająca się w stanie początkowym osiąga ten sam stan przekonania co [Prawo,Lewo,Ssanie], a mianowicie {5,7} . Rozważmy teraz stan wiary osiągnięty przez [Z lewej], a mianowicie {1,3,5,7}. Oczywiście nie jest to identyczne z {5,7} , ale jest to nadzbiór. Możemy odrzucić (przyciąć) każdy taki superzbiór stanów przekonań. Czemu? Ponieważ rozwiązanie z {1,3,5,7} musi być rozwiązaniem dla każdego z poszczególnych stanów 1, 3, 5 i 7, a więc jest rozwiązaniem dla dowolnej kombinacji tych poszczególnych stanów, np. {5 ,7}; dlatego nie musimy próbować rozwiązać {1,3,5,7}, możemy skoncentrować się na próbie rozwiązania ściśle łatwiejszego stanu wiary {5,7}. I odwrotnie, jeśli {1,3,5,7} zostało już wygenerowane i uznane za możliwe do rozwiązania, to każdy podzbiór, taki jak {5,7} , jest gwarantowany. (Jeśli mam rozwiązanie, które działa, gdy jestem bardzo zdezorientowany co do tego, w jakim się jestem stanie, będzie nadal działać, gdy jestem mniej zdezorientowany.) Ten dodatkowy poziom przycinania może znacznie poprawić skuteczność rozwiązywania problemów bezczujnikowych. Jednak nawet przy tym ulepszeniu, bezczujnikowe rozwiązywanie problemów, jak to opisaliśmy, rzadko jest możliwe w praktyce. Jedną z kwestii jest ogrom przestrzeni stanów przekonań — widzieliśmy w poprzednim rozdziale, że często przestrzeń poszukiwań o rozmiarze N jest zbyt duża, a teraz mamy przestrzenie poszukiwań o rozmiarze 2N . Ponadto każdy element przestrzeni wyszukiwania to zestaw do N elementów. W przypadku dużego N nie będziemy w stanie przedstawić nawet jednego stanu przekonań bez wyczerpania pamięci. Jednym z rozwiązań jest przedstawienie stanu przekonań za pomocą bardziej zwięzłego opisu. W języku angielskim moglibyśmy powiedzieć, że agent nie wie „Nic” w stanie początkowym; po przesunięciu w lewo możemy powiedzieć „Nie w skrajnej prawej kolumnie” i tak dalej. Rozdział 7 wyjaśnia, jak to zrobić w formalnym schemacie reprezentacji. Innym podejściem jest unikanie standardowych algorytmów wyszukiwania, które traktują stany przekonań jako czarne skrzynki, tak jak każdy inny stan problemowy. Zamiast tego możemy zajrzeć do wnętrza stanów przekonań i opracować przyrostowe algorytmy wyszukiwania stanów przekonań, które budują rozwiązanie ol_lowerromann świat próżni bezczujnikowej, początkowy stan przekonań to {1,2,3,4,5,6,7,8} i musimy znaleźć sekwencję akcji, która działa we wszystkich 8 stanach. Możemy to zrobić, najpierw znajdując rozwiązanie, które działa dla stanu 1; następnie sprawdzamy, czy działa dla stanu 2; jeśli nie, wróć i znajdź inne rozwiązanie dla stanu 1 i tak dalej. Podobnie jak wyszukiwanie AND–OR musi znaleźć rozwiązanie dla każdej gałęzi w węźle AND, ten algorytm musi znaleźć rozwiązanie dla każdego stanu w stanie przekonania; różnica polega na tym, że wyszukiwanie AND–OR może znaleźć inne rozwiązanie dla każdej gałęzi, podczas gdy przyrostowe wyszukiwanie stanów przekonań musi znaleźć jedno rozwiązanie, które działa dla wszystkich stanów. Główną zaletą podejścia przyrostowego jest to, że zazwyczaj jest ono w stanie szybko wykryć niepowodzenie – gdy stan przekonania jest nierozwiązywalny, zwykle jest tak, że mały podzbiór stanu przekonania, składający się z kilku pierwszych zbadanych stanów, jest również nierozwiązywalny. . W niektórych przypadkach prowadzi to do przyspieszenia proporcjonalnego do wielkości stanów przekonań, które same mogą być tak duże, jak sama przestrzeń stanów fizycznych.

Przejdziemy teraz do problemu częściowej obserwowalności, gdzie percepcje agenta nie wystarczają do określenia dokładnego stanu. Oznacza to, że część działań agenta będzie miała na celu zmniejszenie niepewności co do obecnego stanu

Rozważmy śliski świat próżni, który jest identyczny ze zwykłym (niezmiennym) światem próżni, z tą różnicą, że ruchy czasami kończą się niepowodzeniem, pozostawiając agenta w tym samym miejscu. Na przykład przesunięcie w prawo w stanie 1 prowadzi do stanu przekonań {1,2}. Rysunek przedstawia część wykresu wyszukiwania; widać, że nie ma już acyklicznych rozwiązań ze stanu 1, a ANDORSEARCH wróci z porażką.

Istnieje jednak cykliczne rozwiązanie, które polega na próbowaniu Prawidłowo, dopóki nie zadziała. Możemy to wyrazić za pomocą nowej konstrukcji while:

[Suck,while State = 5 do Right, Suck]

lub dodając etykietę oznaczającą część planu i odnosząc się do tej etykiety później:

[Suck,L1 : Right, if State = 5 then L1 else Suck]

Kiedy plan cykliczny jest rozwiązaniem? Minimalnym warunkiem jest to, że każdy liść jest stanem docelowym i że liść jest osiągalny z każdego punktu planu. Oprócz tego musimy rozważyć przyczynę niedeterminizmu. Jeśli rzeczywiście jest tak, że mechanizm napędowy robota próżniowego przez jakiś czas działa, ale w innych przypadkach ślizga się losowo i niezależnie, to agent może być pewien, że jeśli czynność zostanie powtórzona wystarczająco dużo razy, w końcu zadziała i plan zadziała. odnieść sukces. Ale jeśli niedeterminizm jest spowodowany jakimś niezauważonym faktem dotyczącym robota lub środowiska — na przykład pękł pasek napędowy i robot nigdy się nie poruszy — to powtórzenie czynności nie pomoże. Jednym ze sposobów zrozumienia tej decyzji jest stwierdzenie, że początkowe sformułowanie problemu (w pełni obserwowalne, niedeterministyczne) jest porzucane na rzecz innego sformułowania (częściowo obserwowalnego, deterministycznego), w którym niepowodzenie planu cyklicznego przypisuje się nieobserwowanej właściwości popędu pasek.

Jak znaleźć te przypadkowe rozwiązania problemów niedeterministycznych? Jak wcześniej zaczynamy od skonstruowania drzew poszukiwań, ale tutaj drzewa mają inny charakter. W środowisku deterministycznym jedyne rozgałęzienie jest wprowadzane przez własne wybory agenta w każdym stanie: mogę wykonać tę akcję lub inną akcję. Nazywamy te węzły OR węzłami. W świecie próżni, na przykład, w węźle OR agent wybiera Lewo, Prawo lub Ssanie. W środowisku anondeterministycznym rozgałęzienie jest również wprowadzane przez wybór wyniku dla każdego działania. Nazywamy te węzły AND węzłami. Na przykład działanie Suck w stanie 1 skutkuje stanem przekonania , więc agent musiałby znaleźć plan dla stanu 5 i dla stanu 7. Te dwa rodzaje węzłów są naprzemienne, co prowadzi do drzewa AND–OR, jak pokazano na rysunku.

Rozwiązaniem problemu wyszukiwania AND-OR jest poddrzewo pełnego drzewa wyszukiwania, które (1) ma węzeł celu na każdym liściu, (2) określa jedną akcję w każdym z węzłów OR i (3) zawiera każdą gałąź wyniku w każdym z jego węzłów AND. Rozwiązanie pokazano na rysunku pogrubionymi liniami; odpowiada planowi podanemu w Równaniu (4.3) . Rysunek przedstawia rekurencyjny algorytm do przeszukiwania grafów AND–OR. Jednym z kluczowych aspektów algorytmu jest sposób, w jaki radzi sobie z cyklami, które często pojawiają się w problemach niedeterministycznych (np. jeśli działanie czasami nie przynosi efektu lub jeśli niezamierzony skutek może zostać skorygowany). Jeśli aktualny stan jest identyczny ze stanem na ścieżce od korzenia, to wraca z niepowodzeniem. Nie oznacza to, że nie ma rozwiązania z obecnego stanu; oznacza to po prostu, że jeśli istnieje rozwiązanie niecykliczne, musi być ono osiągalne z wcześniejszego wcielenia obecnego stanu, aby nowe wcielenie można było odrzucić. Dzięki tej kontroli upewniamy się, że algorytm kończy się w każdej skończonej przestrzeni stanów, ponieważ każda ścieżka musi osiągnąć cel, ślepy zaułek lub powtarzający się stan. Zauważ, że algorytm nie sprawdza, czy aktualny stan jest powtórzeniem stanu na jakiejś innej ścieżce od korzenia, co ma znaczenie dla wydajności.

Wykresy AND–OR mogą być eksplorowane albo wszerz albo w pierwszej kolejności. Pojęcie funkcji heurystycznej musi zostać zmodyfikowane, aby oszacować koszt rozwiązania warunkowego, a nie sekwencji, ale pojęcie dopuszczalności pozostaje nadal i istnieje analogia algorytmu A* do znajdowania optymalnych rozwiązań.

Świat próżni  ma osiem stanów, jak pokazano na rysunku

Istnieją trzy akcje — Prawo, Lewo i Ssanie — a celem jest oczyszczenie całego brudu (stany 7 i 8). Jeśli środowisko jest w pełni obserwowalne, deterministyczne i całkowicie znane, to problem można łatwo rozwiązać dowolnym algorytmem z rozdziału 3, a rozwiązaniem jest sekwencja działań. Na przykład, jeśli stan początkowy wynosi 1, to sekwencja działań [Ssanie, Prawo, Ssanie] osiągnie stan docelowy 8.

Załóżmy teraz, że wprowadzamy niedeterminizm w postaci potężnego, ale nieobliczalnego odkurzacza. W nieobliczalnym świecie próżni akcja Ssania działa w następujący sposób:

*Po nałożeniu na brudny kwadrat, działanie czyści kwadrat, a czasem usuwa również brud z sąsiedniego kwadratu.

* Po nałożeniu na czysty kwadrat, działanie czasami powoduje osadzanie brudu na dywanie.

Aby precyzyjnie sformułować ten problem, musimy uogólnić pojęcie modelu przejścia z rozdziału 3 . Zamiast definiować model przejścia przez funkcję WYNIK, która zwraca pojedynczy stan wyniku, używamy funkcji WYNIKI, która zwraca zestaw możliwych stanów wyniku. Na przykład w świecie błędnej próżni akcja Suck w stanie 1 czyści albo tylko bieżącą lokalizację, albo obie lokalizacje:

RESULTS(1, Suck) = {5,7}

Jeśli zaczniemy w stanie 1, żadna pojedyncza sekwencja działań nie rozwiąże problemu, ale następujący plan warunkowy tak:

[Suck, if State = 5 to [Right, Suck] else [ ]] .

Widzimy tutaj, że plan warunkowy może zawierać kroki „jeśli-to-inne”; oznacza to, że rozwiązania są drzewami, a nie sekwencjami. Tutaj warunek w instrukcji if sprawdza, jaki jest aktualny stan; jest to coś, co agent będzie mógł obserwować w czasie wykonywania, ale nie wie w czasie planowania. Alternatywnie moglibyśmy mieć sformułowanie testujące raczej percepcję niż stan. Wiele problemów w rzeczywistym, fizycznym świecie to problemy przypadkowe, ponieważ dokładne przewidzenie przyszłości jest niemożliwe. Z tego powodu wiele osób ma otwarte oczy podczas chodzenia.