Miesiąc: wrzesień 2021

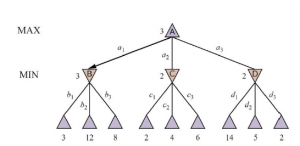
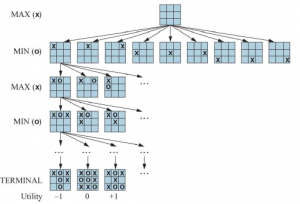
Wiele popularnych gier pozwala na więcej niż dwóch graczy. Przyjrzyjmy się, jak rozszerzyć ideę minimaxa na gry wieloosobowe. Jest to proste z technicznego punktu widzenia, ale rodzi kilka interesujących nowych kwestii koncepcyjnych. Najpierw musimy zastąpić pojedynczą wartość dla każdego węzła wektorem wartości. Na przykład w grze trzyosobowej z graczami A, B i C, wektor (v_A.v_B,v_C) jest powiązany z każdym węzłem. W przypadku stanów końcowych wektor ten podaje użyteczność stanu z punktu widzenia każdego gracza. (W grach dla dwóch graczy o sumie zerowej dwuelementowy wektor można zredukować do pojedynczej wartości, ponieważ wartości są zawsze przeciwne). Najprostszym sposobem na zaimplementowanie tego jest zwrócenie przez funkcję UTILITY wektora narzędzi. Teraz musimy rozważyć stany nieterminalne. Rozważ węzeł zaznaczony X w drzewie gry pokazanym na rysunku.

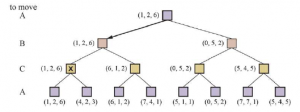
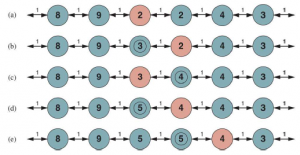
W tym stanie gracz C decyduje, co robić. Te dwie opcje prowadzą do stanów końcowych z wektorami użyteczności (v_A = 1.v_B = 2 ,v_C = 6) i (v_A = ₄ .v_B = 2,v_C = 3) . Ponieważ 6 jest większe niż 3, C powinien wybrać pierwszy ruch. Oznacza to, że jeśli stan X zostanie osiągnięty, kolejne odtwarzanie doprowadzi do stanu końcowego  z narzędziami (v_A = 1.v_B = 2 ,v_C = 6)  . Dlatego wartością kopii zapasowej X jest ten wektor. Ogólnie rzecz biorąc, wartość węzła n w kopii zapasowej jest wektorem użyteczności stanu następcy z najwyższą wartością dla gracza wybierającego w n.

Każdy, kto gra w gry wieloosobowe, takie jak Dyplomacja czy Osadnicy z Catanu, szybko uświadamia sobie, że dzieje się o wiele więcej niż w grach dwuosobowych. Gry wieloosobowe zwykle obejmują sojusze, formalne lub nieformalne, między graczami. Sojusze są zawierane i łamane w miarę postępu gry. Jak mamy rozumieć takie zachowanie? Czy sojusze są naturalną konsekwencją optymalnych strategii dla każdego gracza w grze wieloosobowej? Okazuje się, że mogą.

Załóżmy na przykład, że A i B są na słabych pozycjach, a C na silniejszej pozycji. Wtedy często optymalne jest, aby zarówno A, jak i B atakowały C, a nie siebie nawzajem, aby C nie zniszczyło każdego z nich z osobna. W ten sposób współpraca wyłania się z czysto egoistycznego zachowania.

Oczywiście, gdy tylko C słabnie pod wspólnym natarciem, sojusz traci swoją wartość, a A lub B mogą naruszyć porozumienie. W niektórych przypadkach jawne sojusze jedynie konkretyzują to, co i tak by się wydarzyło. W innych przypadkach zerwanie sojuszu wiąże się z piętnem społecznym, więc gracze muszą zrównoważyć bezpośrednią przewagę zerwania sojuszu z długoterminową wadą bycia postrzeganym jako niegodny zaufania. Jeśli gra nie ma sumy zerowej, współpraca może również mieć miejsce tylko z dwoma graczami. Załóżmy na przykład, że istnieje stan terminala z narzędziami (vA = 1000 i vB = 1000), że 1000 jest najwyższą możliwą użytecznością dla każdego gracza. Wtedy optymalna strategia polega na tym, aby obaj gracze zrobili wszystko, co możliwe, aby osiągnąć ten stan – to znaczy, że gracze będą automatycznie współpracować, aby osiągnąć wspólnie pożądany cel.

Teraz, gdy możemy obliczyć MINIMAX(y), możemy przekształcić to w algorytm wyszukiwania, który znajduje najlepszy ruch dla MAX, próbując wszystkie działania i wybierając to, którego wynikowy stan ma najwyższą wartość MINIMAX. Rysunek przedstawia algorytm. Jest to algorytm rekurencyjny, który przechodzi aż do liści drzewa, a następnie tworzy kopię zapasową wartości minimax w drzewie, gdy rekurencja się rozwija. Na przykład na rysunku wcześniej algorytm najpierw przechodzi w dół do trzech dolnych lewych węzłów i używa na nich funkcji UTILITY, aby odkryć, że ich wartości wynoszą odpowiednio 3, 12 i 8. Następnie pobiera minimalną z tych wartości, 3, i zwraca ją jako kopię zapasową wartości node . Podobny proces daje w kopii zapasowej wartości 2 dla i 2 dla C . Na koniec przyjmujemy maksymalnie 3, 2 i 2, aby uzyskać kopię zapasową wartości 3 dla węzła głównego.

Algorytm minimax wykonuje pełną eksplorację drzewa gry w głąb. Jeżeli maksymalna głębokość drzewa wynosi m i w każdym punkcie są dozwolone ruchy, to złożoność czasowa algorytmu minimax wynosi O(b^m) . Złożoność przestrzeni wynosi O(bm) dla algorytmu, który generuje wszystkie akcje na raz, lub O(m) dla algorytmu, który generuje akcje pojedynczo. Wykładnicza złożoność sprawia, że MINIMAX jest niepraktyczny dla złożonych gier; na przykład szachy mają współczynnik rozgałęzienia około 35, a średnia gra ma głębokość około 80 warstw i nie jest możliwe przeszukanie 35⁸⁰ ≈ 10¹²³ stanów. MINIMAX służy jednak jako podstawa do matematycznej analizy gier. Aproksymując analizę minimaksową na różne sposoby, możemy uzyskać bardziej praktyczne algorytmy.

MAX chce znaleźć sekwencję działań prowadzących do wygranej, ale MIN ma na ten temat coś do powiedzenia. Oznacza to, że strategia MAX musi być planem warunkowym – strategią warunkową, określającą reakcję na każdy z możliwych ruchów MIN. W grach, które mają wynik binarny (wygrana lub przegrana), możemy użyć wyszukiwania AND–OR (strona 125), aby wygenerować plan warunkowy. W rzeczywistości w takich grach definicja strategii wygrywającej w grze jest identyczna z definicją rozwiązania niedeterministycznego problemu planowania: w obu przypadkach pożądany wynik musi być zagwarantowany bez względu na to, co zrobi „druga strona”. W przypadku gier z wieloma wynikami, potrzebujemy nieco bardziej ogólnego algorytmu zwanego wyszukiwaniem minimaksowym.

Rozważ trywialną grę z rysunku 5.2. Możliwe ruchy dla MAX w węźle głównym są oznaczone jako a1, a2 i a3. Możliwe odpowiedzi na a1 dla MIN to b1 , b2 , b3 i tak dalej. Ta konkretna gra kończy się po jednym ruchu, każdy o MAX i MIN. (UWAGA: W niektórych grach słowo „ruch” oznacza, że ​​obaj gracze podjęli działanie; dlatego słowo ply jest używane do jednoznacznego oznaczenia jednego ruchu jednego gracza, co przenosi nas o jeden poziom głębiej w drzewo gry). stany terminali w tej grze wahają się od 2 do 14.

Mając dane drzewo gry, optymalną strategię można określić, wyliczając wartość minimaksową każdego stanu w drzewie, którą zapisujemy jako MINIMAX(y). Wartość minimax to użyteczność (dla MAX) bycia w tym stanie, przy założeniu, że obaj gracze grają optymalnie od tego momentu do końca gry. Wartość minimax stanu terminala to tylko jego użyteczność. W stanie nieterminalnym MAX woli przejść do stanu o maksymalnej wartości, gdy nadchodzi kolej MAXa na ruch, a MIN preferuje stan o minimalnej wartości (czyli minimalnej wartości dla MAX, a tym samym maksymalnej wartości dla MIN). Więc mamy:

Zastosujmy te definicje do drzewa gry na rysunku 5.2. Węzły końcowe na dolnym poziomie uzyskują swoje wartości użytkowe z funkcji UTILITY w grze. Pierwszy węzeł MIN, oznaczony etykietą , ma trzy stany następcze o wartościach 3, 12 i 8, więc jego wartość minimax wynosi 3. Podobnie pozostałe dwa węzły MIN mają wartość minimax 2. Węzeł główny jest węzłem MAX; jego stany następcze mają wartości minimax 3, 2 i 2; więc ma wartość minimaksową równą 3. Możemy również zidentyfikować decyzję minimaksową u korzenia: akcja a1 jest optymalnym wyborem dla MAX, ponieważ prowadzi do stanu o najwyższej wartości minimaksowej.

Ta definicja optymalnej gry dla MAX zakłada, że ​​MIN również gra optymalnie. Co jeśli MIN nie gra optymalnie? Wtedy MAX poradzi sobie co najmniej tak dobrze, jak przeciwko optymalnemu graczowi, a może nawet lepiej. Nie oznacza to jednak, że zawsze najlepiej jest zagrać optymalny ruch minimaksowy w obliczu nieoptymalnego przeciwnika. Rozważ sytuację, w której optymalna gra obu stron doprowadzi do remisu, ale jest jeden ryzykowny ruch dla MAX, który prowadzi do stanu, w którym jest 10 możliwych ruchów odpowiedzi na MIN, które wydają się rozsądne, ale 9 z nich to strata dla MIN, a jeden to strata dla MAX. Jeśli MAX uważa, że ​​MIN nie ma wystarczającej mocy obliczeniowej, aby odkryć optymalny ruch, MAX może chcieć spróbować ryzykownego ruchu, ponieważ szansa 9/10 na wygraną jest lepsza niż pewien remis.

Gry najczęściej badane w ramach sztucznej inteligencji (takie jak szachy i go) to gry, które teoretycy gier nazywają deterministycznymi, dwuosobowymi, rozgrywającymi się na zmianę, z doskonałą informacją, grami o sumie zerowej. „Doskonała informacja” jest synonimem „w pełni obserwowalnej”, a „suma zerowa” oznacza, że to, co jest dobre dla jednego gracza, jest tak samo złe dla drugiego: nie ma wyniku „wygrana-wygrana”. W grach często używamy terminu move jako synonimu „akcji” i pozycji jako synonimu „stanu”. Zadzwonimy do naszych dwóch graczy MAX i MIN, z powodów, które wkrótce staną się oczywiste. MAX porusza się jako pierwszy, a następnie gracze na zmianę poruszają się, aż gra się skończy. Na koniec gry zwycięski gracz otrzymuje punkty, a przegrany otrzymuje kary. Gra może być formalnie zdefiniowana za pomocą następujących elementów:

* S₀ : Stan początkowy, który określa, jak gra jest skonfigurowana na początku.

* TO-MOVE(s): Gracz, którego kolej ma się poruszyć w stanie .

* ACTIONS : Zestaw prawidłowych ruchów w stanie .

* RESULTS(s,a): Model przejścia, który definiuje stan wynikający z podjęcia działań w stanie .

* IS-TERMINAL(s): Test terminala, który jest prawdziwy po zakończeniu gry i fałszywy w przeciwnym razie. Stany, w których gra się zakończyła, nazywane są stanami końcowymi.

* UTILITY(s,p) : Funkcja użyteczności (nazywana również funkcją celu lub funkcją wypłaty), która definiuje ostateczną wartość liczbową dla gracza, gdy gra kończy się w stanie terminala. W szachach wynikiem jest wygrana, przegrana lub remis z wartościami 1 , 0 lub 1/2 . Niektóre gry mają szerszy zakres możliwych wyników – na przykład wypłaty w tryktraku wahają się od 0 do 192 .

Podobnie jak wcześniej , stan początkowy, funkcja AKCJE i funkcja WYNIK definiują graf przestrzeni stanów – graf, w którym wierzchołki są stanami, krawędziami są ruchami, a stan może być osiągnięty wieloma ścieżkami. Możemy nałożyć drzewo poszukiwań na część tego wykresu, aby określić, jaki ruch wykonać. Kompletne drzewo gry definiujemy jako drzewo wyszukiwania, które podąża za każdą sekwencją ruchów aż do stanu terminala. Drzewo gry może być nieskończone, jeśli sama przestrzeń stanów jest nieograniczona lub jeśli reguły gry pozwalają na nieskończenie powtarzające się pozycje. Rysunek przedstawia część drzewa gry w kółko i krzyżyk (kółko i krzyżyk). Od stanu początkowego MAX ma dziewięć możliwych ruchów. Gra naprzemiennie polega na tym, że MAX umieszcza X MIN, umieszcza O, aż dotrzemy do węzłów liści odpowiadających stanom końcowym, tak że jeden gracz ma trzy kwadraty z rzędu lub wszystkie kwadraty są wypełnione. Liczba na każdym węźle liścia wskazuje wartość użytkową stanu końcowego z punktu widzenia MAX; wysokie wartości są dobre dla MAX, a złe dla MIN (w ten sposób gracze otrzymują swoje nazwy).

W przypadku gry w kółko i krzyżyk drzewo gry jest stosunkowo mniejsze niż 9! = 362 880 węzłów końcowych (tylko 5478 różnych stanów). Ale w szachach istnieją ponad węzły, więc drzewo gry najlepiej traktować jako konstrukt teoretyczny, którego nie możemy zrealizować w świecie fizycznym.

Istnieją co najmniej trzy stanowiska, które możemy przyjąć w stosunku do środowisk wieloagentowych. Pierwszym stanowiskiem, odpowiednim w przypadku bardzo dużej liczby podmiotów, jest rozważenie ich łącznie jako gospodarki, co pozwala nam na przewidywanie, że rosnący popyt spowoduje wzrost cen, bez konieczności przewidywania działania jakichkolwiek indywidualny agent. Po drugie, moglibyśmy traktować podmioty przeciwne tylko jako część środowiska – część, która sprawia, że ​​środowisko jest niedeterministyczne. Ale jeśli modelujemy przeciwników w taki sam sposób, w jaki, powiedzmy, deszcz czasami pada, a czasami nie, tracimy ideę, że nasi przeciwnicy aktywnie próbują nas pokonać, podczas gdy deszcz rzekomo nie ma takiego zamiaru. Trzecie stanowisko polega na wyraźnym modelowaniu przeciwników za pomocą technik przeszukiwania drzew przeciwnika. To właśnie obejmuje ten rozdział. Zaczynamy od ograniczonej klasy gier i definiujemy optymalny ruch oraz algorytm do jego znajdowania. Przeszukiwanie minimaksowe, uogólnienie przeszukiwania AND–OR. Pokazujemy, że przycinanie sprawia, że ​​wyszukiwanie jest bardziej wydajne, ignorując części drzewa wyszukiwania, które nie mają wpływu na optymalny ruch. W nietrywialnych grach zwykle nie mamy wystarczająco dużo czasu, aby znaleźć optymalny ruch (nawet przy przycinaniu); w pewnym momencie będziemy musieli przerwać poszukiwania. Dla każdego stanu, w którym postanowiliśmy przestać szukać, pytamy, kto wygrywa. Aby odpowiedzieć na to pytanie, mamy wybór: możemy zastosować heurystyczną funkcję oceny, aby oszacować, kto wygrywa na podstawie cech stanu, lub możemy uśrednić wyniki wielu szybkich symulacji gry z tego stanu wszystkie droga do końca . Omawiamy gry, które zawierają element losowy (poprzez rzucanie kośćmi lub tasowanie kart), i omawiamy gry z niedoskonałymi informacjami (takie jak poker i brydż, gdzie nie wszystkie karty są widoczne dla wszystkich graczy).

Badamy środowiska, w których inni agenci spiskują przeciwko nam. W tym rozdziale omówimy środowiska konkurencyjne, w których dwóch lub więcej agentów ma sprzeczne cele, co powoduje problemy z wyszukiwaniem przeciwników. Zamiast zajmować się chaosem potyczek w prawdziwym świecie, skoncentrujemy się na grach, takich jak szachy, Go i poker. Dla badaczy sztucznej inteligencji uproszczona natura tych gier jest plusem: stan gry jest łatwy do przedstawienia, a agenci są zwykle ograniczeni do niewielkiej liczby działań, których efekty są określone przez precyzyjne reguły. Gry fizyczne, takie jak krokiet czy hokej, mają bardziej skomplikowane opisy, większy zakres możliwych akcji i raczej nieprecyzyjne reguły określające legalność działań. Z wyjątkiem robotów piłkarskich, te fizyczne gry nie wzbudziły dużego zainteresowania społeczności AI.

Zbadaliśmy algorytmy wyszukiwania problemów w środowiskach częściowo obserwowalnych, niedeterministycznych, nieznanych i ciągłych.

* Lokalne metody wyszukiwania, takie jak wspinaczka górska, przechowują w pamięci tylko niewielką liczbę stanów. Zostały one zastosowane w problemach optymalizacyjnych, gdzie ideą jest znalezienie stanu o wysokiej punktacji, bez martwienia się o ścieżkę do tego stanu. Opracowano kilka stochastycznych algorytmów wyszukiwania lokalnego, w tym symulowane wyżarzanie, które zwraca optymalne rozwiązania przy odpowiednim harmonogramie chłodzenia.

* Wiele lokalnych metod wyszukiwania stosuje się również do problemów w przestrzeniach ciągłych. Programowanie liniowe i zagadnienia optymalizacji wypukłej podlegają pewnym ograniczeniom dotyczącym kształtu przestrzeni stanów i charakteru funkcji celu oraz dopuszczają algorytmy wielomianowe, które często są niezwykle wydajne w praktyce. W przypadku niektórych matematycznie dobrze sformułowanych problemów możemy znaleźć maksimum za pomocą rachunku różniczkowego, aby znaleźć, gdzie gradient wynosi zero; w przypadku innych problemów musimy zadowolić się gradientem empirycznym, który mierzy różnicę sprawności między dwoma pobliskimi punktami.

* Algorytm ewolucyjny to stochastyczne poszukiwanie wspinaczki, w którym utrzymywana jest populacja stanów. Nowe stany generowane są przez mutację oraz przez crossover, który łączy pary stanów.

* W środowiskach niedeterministycznych agenci mogą zastosować wyszukiwanie AND-OR, aby wygenerować plany warunkowe, które osiągną cel, niezależnie od tego, jakie wyniki wystąpią podczas wykonywania.

* Gdy środowisko jest częściowo obserwowalne, stan przekonań reprezentuje zestaw możliwych stanów, w których może znajdować się agent. * Standardowe algorytmy wyszukiwania można zastosować bezpośrednio do przestrzeni stanów przekonań, aby rozwiązać problemy bezczujnikowe, a wyszukiwanie stanów przekonań AND–LUB potrafi rozwiązywać ogólne, częściowo obserwowalne problemy. Algorytmy przyrostowe, które konstruują rozwiązania stan po stanie w stanie przekonań, są często bardziej wydajne.

* Problemy z eksploracją pojawiają się, gdy agent nie ma pojęcia o stanach i działaniach swojego otoczenia. W środowiskach, w których można bezpiecznie eksplorować, agenci wyszukiwania online mogą zbudować mapę i znaleźć cel, jeśli taki istnieje. Aktualizacja szacunków heurystycznych na podstawie doświadczenia zapewnia skuteczną metodę ucieczki od lokalnych minimów.

Początkowa ignorancja agentów wyszukiwania online daje kilka możliwości uczenia się. Po pierwsze, agenci uczą się „mapy” środowiska – a dokładniej wyniku każdego działania w każdym stanie – po prostu przez rejestrowanie każdego ze swoich doświadczeń. Po drugie, lokalni agenci wyszukiwania uzyskują dokładniejsze oszacowania kosztów każdego stanu za pomocą lokalnych reguł aktualizacji, jak w LRTA*. Pokazujemy, że te aktualizacje ostatecznie zbiegają się do dokładnych wartości dla każdego stanu, pod warunkiem, że agent we właściwy sposób eksploruje przestrzeń stanów. Gdy znane są dokładne wartości, optymalne decyzje można podejmować po prostu, przechodząc do następcy o najniższych kosztach — to znaczy, że czysta wspinaczka górska jest wówczas optymalną strategią. Jeśli zastosowałeś się do naszej sugestii, aby prześledzić zachowanie ONLINE-DFS-AGENT w środowisku z rysunku 4.19, zauważysz, że agent nie jest zbyt jasny. Na przykład, po zobaczeniu, że akcja W górę przechodzi od (1,1) do (1,2), agent nadal nie ma pojęcia, że ​​akcja W dół wraca do (1,1) lub że akcja W górę również przechodzi od (2,1) do (2,2), od (2,2) do (2,3) i tak dalej. Ogólnie rzecz biorąc, chcielibyśmy, aby agent dowiedział się, że Up zwiększa współrzędną -, chyba że na drodze jest ściana, że ​​Down ją zmniejsza i tak dalej. Aby tak się stało, potrzebujemy dwóch rzeczy. Po pierwsze, potrzebujemy formalnej i wyraźnie manipulowalnej reprezentacji tego rodzaju ogólnych reguł; do tej pory ukrywaliśmy informacje w czarnej skrzynce zwanej funkcją RESULT. Temu zagadnieniu poświęcone są rozdziały od 8 do 11. Po drugie, potrzebujemy algorytmów, które potrafią skonstruować odpowiednie reguły ogólne na podstawie konkretnych obserwacji dokonanych przez agenta. Zostały one omówione później. Jeśli przewidujemy, że będziemy wezwani do rozwiązania wielu podobnych problemów w przyszłości, warto zainwestować czas (i pamięć), aby ułatwić te przyszłe poszukiwania.

Można to zrobić na kilka sposobów, z których wszystkie należą do kategorii wyszukiwania przyrostowego. Moglibyśmy zachować drzewo wyszukiwania w pamięci i ponownie wykorzystać jego niezmienione części w nowym problemie. Moglibyśmy zachować heurystyczne wartości h i aktualizować je w miarę zdobywania nowych informacji — albo dlatego, że świat się zmienił, albo dlatego, że obliczyliśmy lepsze oszacowanie. Lub możemy zachować wartości g najlepszej ścieżki, używając ich do złożenia nowego rozwiązania i aktualizując je, gdy świat się zmieni.

Podobnie jak wyszukiwanie w głąb, wyszukiwanie ze wspinaczką ma właściwość lokalizacji w rozwinięciach węzłów. W rzeczywistości, ponieważ przechowuje tylko jeden aktualny stan w pamięci, wyszukiwanie wspinaczkowe jest już algorytmem wyszukiwania online! Niestety podstawowy algorytm nie jest zbyt dobry do eksploracji, ponieważ pozostawia agenta siedzącego na lokalnych maksimach bez miejsca, do którego mógłby się udać. Ponadto nie można używać losowych restartów, ponieważ agent nie może teleportować się do nowego stanu startowego. Zamiast losowych restartów, można rozważyć skorzystanie z przypadkowego spaceru w celu zbadania otoczenia. Spacer losowy po prostu wybiera losowo jedną z dostępnych akcji z bieżącego stanu; pierwszeństwo mogą mieć działania, które nie zostały jeszcze wypróbowane. Łatwo jest udowodnić, że losowy spacer w końcu znajdzie cel lub dokończy jego eksplorację, pod warunkiem, że przestrzeń jest skończona i bezpieczna do eksploracji. Z drugiej strony proces może być bardzo powolny. Rysunek  pokazuje środowisko, w którym błądzenie losowe wymaga wykładniczo wielu kroków, aby znaleźć cel, ponieważ dla każdego stanu w górnym wierszu z wyjątkiem S, postęp wstecz jest dwa razy bardziej prawdopodobny niż postęp w przód. Przykład jest oczywiście wymyślony, ale istnieje wiele rzeczywistych przestrzeni stanów, których topologia powoduje tego rodzaju „pułapki” na losowe spacery.

Wspinanie się po wzgórzach za pomocą pamięci, a nie przypadkowości, okazuje się bardziej skutecznym podejściem. Podstawowym pomysłem jest przechowywanie „aktualnego najlepszego oszacowania” H(ów) kosztów, aby osiągnąć cel z każdego odwiedzonego stanu. H(s) zaczyna być tylko oszacowaniem heurystycznym h(s) i jest aktualizowane, gdy agent zdobywa doświadczenie w przestrzeni stanów. Rysunek pokazuje prosty przykład w jednowymiarowej przestrzeni stanów. W (a) agent wydaje się utknąć w płaskim lokalnym minimum w stanie czerwonym. Zamiast pozostawać tam, gdzie jest, agent powinien podążać drogą, która wydaje się być najlepszą ścieżką do celu, biorąc pod uwagę aktualne szacunki kosztów dla sąsiadów. Szacowany koszt dotarcia do celu przez sąsiada s’ to koszt dotarcia do s’ plus szacowany koszt dotarcia do celu stamtąd, czyli .c(s,a,s’) + H(s’ ) . W tym przykładzie są dwie akcje, z szacowanymi kosztami po lewej i po prawej stronie, więc wydaje się, że najlepiej przejść w prawo.

W punkcie (b) wyraźnie widać, że szacunek kosztów 2 dla stanu czerwonego w punkcie (a) był zbyt optymistyczny. Ponieważ najlepszy ruch kosztował 1 i doprowadził do stanu, który jest co najmniej 2 kroki od celu, czerwony stan musi znajdować się co najmniej 3 kroki od celu, więc jego H należy odpowiednio zaktualizować, jak pokazano na rysunku (b). . Kontynuując ten proces, agent będzie się jeszcze dwa razy poruszał tam i z powrotem, za każdym razem aktualizując H i „spłaszczając” lokalne minimum, aż ucieknie w prawo.

Agenta realizującego ten schemat, który nazywa się uczeniem się A* w czasie rzeczywistym (LRTA*), pokazano na rysunku. Podobnie jak ONLINE-DFS-AGENT, buduje mapę środowiska w tabeli wyników. Aktualizuje oszacowanie kosztów dla stanu, który właśnie opuścił, a następnie wybiera „najwyraźniej najlepszy” ruch zgodnie z aktualnymi szacunkami kosztów. Ważnym szczegółem jest to, że zakłada się, że działania, które nie zostały jeszcze wypróbowane w danym stanie, prowadzą natychmiast do celu przy możliwie najmniejszych kosztach, czyli h(s). Ten optymizm w warunkach niepewności skłania agenta do poszukiwania nowych, potencjalnie obiecujących ścieżek.

Agent LRTA* gwarantuje znalezienie celu w każdym ograniczonym, bezpiecznym środowisku. Jednak w przeciwieństwie do A*, nie jest ona zupełna dla nieskończonych przestrzeni stanów — są przypadki, w których może być wyprowadzona na nieskończenie błąd. W najgorszym przypadku może badać środowisko składające się z n stanów w krokach O(n²), ale często działa znacznie lepiej. Agent LRTA* jest tylko jednym z dużej rodziny agentów online, które można zdefiniować, określając na różne sposoby regułę wyboru akcji i regułę aktualizacji. Omawiamy tę rodzinę, opracowaną pierwotnie dla środowisk stochastycznych

Po każdej akcji agent online w obserwowalnym środowisku otrzymuje percept informujący go, jaki stan osiągnął; na podstawie tych informacji może uzupełnić swoją mapę środowiska. Zaktualizowana mapa jest następnie wykorzystywana do planowania dalszych kroków. To przeplatanie się planowania i działania oznacza, że ​​algorytmy wyszukiwania online różnią się znacznie od algorytmów wyszukiwania offline, które widzieliśmy wcześniej: algorytmy offline eksplorują swój model przestrzeni stanów, podczas gdy algorytmy online eksplorują świat rzeczywisty. Na przykład A* może rozwinąć węzeł w jednej części przestrzeni, a następnie natychmiast rozwinąć węzeł w odległej części przestrzeni, ponieważ rozwinięcie węzła obejmuje działania symulowane, a nie rzeczywiste. Z drugiej strony algorytm online może odkryć następców tylko dla stanu, który fizycznie zajmuje. Aby uniknąć podróżowania aż do stanu odległego w celu rozszerzenia następnego węzła, wydaje się, że lepiej jest rozszerzać węzły w kolejności lokalnej. Wyszukiwanie według głębokości ma dokładnie tę właściwość, ponieważ (z wyjątkiem sytuacji, gdy algorytm cofa) następny rozwinięty węzeł jest potomkiem poprzedniego rozwiniętego węzła. Internetowy agent eksploracji w głąb (dla deterministycznych, ale nieznanych działań) pokazano na rysunku. Ten agent przechowuje swoją mapę w tabeli result[s,a], która rejestruje stan wynikający z wykonania akcji w state s. (W przypadku działań niedeterministycznych agent może zarejestrować zestaw stanów w wyniku[s,a].) Zawsze, gdy bieżący stan zawiera niezbadane działania, agent próbuje wykonać jedną z nich. Trudność pojawia się, gdy agent wypróbował wszystkie działania w stanie. W trybie wyszukiwania głębokiego offline stan jest po prostu usuwany z kolejki; w wyszukiwarce online agent musi cofnąć się do świata fizycznego. W wyszukiwaniu dogłębnym oznacza to powrót do stanu, z którego agent ostatnio wszedł w obecny stan. Aby to osiągnąć, algorytm przechowuje kolejną tabelę, która dla każdego stanu zawiera poprzednie stany, do których agent jeszcze się nie cofnął. Jeśli agentowi zabrakło stanów, do których może się cofnąć, wyszukiwanie jest zakończone.

Zalecamy czytelnikowi prześledzenie postępu ONLINE-DFS-AGENT po zastosowaniu go w labiryncie przedstawionym na rysunku powyżej. Dość łatwo zauważyć, że w najgorszym przypadku agent przejdzie przez każde łącze w przestrzeni stanów dokładnie dwa razy. W przypadku eksploracji jest to optymalne; z drugiej strony, jeśli chodzi o znalezienie celu, współczynnik konkurencyjności agenta może być arbitralnie zły, jeśli wyrusza na długą wycieczkę, gdy cel znajduje się tuż obok stanu początkowego. Internetowy wariant pogłębiania iteracyjnego rozwiązuje ten problem; dla środowiska, które jest drzewem jednorodnym, stosunek konkurencyjności takiego agenta jest małą stałą. Ze względu na metodę cofania, ONLINE-DFS-AGENT działa tylko w przestrzeniach stanów, w których akcje są odwracalne. Istnieją nieco bardziej złożone algorytmy, które działają w ogólnych przestrzeniach stanów, ale żaden taki algorytm nie ma ograniczonego współczynnika konkurencyjności.