Podobnie jak w przypadku minimaxu, oczywistym przybliżeniem, jakie można zrobić z expectiminimaxem, jest odcięcie wyszukiwania w pewnym momencie i zastosowanie funkcji oceny do każdego liścia. Można by pomyśleć, że funkcje ewaluacyjne w grach takich jak tryktrak powinny być takie same jak funkcje ewaluacyjne w szachach – po prostu muszą dawać wyższe wartości lepszym pozycjom. Ale w rzeczywistości obecność przypadkowych węzłów oznacza, że trzeba być bardziej ostrożnym, co oznaczają wartości.
Rysunek pokazuje, co się dzieje: z funkcją oceny, która przypisuje wartości [1, 2, 3, 4] do liści, ruch a1 jest najlepszy; o wartościach [1, 20, 30, 400] najlepiej jest wykonać ruch a2. W związku z tym program zachowuje się zupełnie inaczej, jeśli dokonamy zmiany niektórych wartości oceny, nawet jeśli kolejność preferencji pozostaje taka sama.
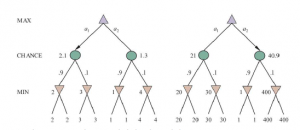
Okazuje się, że aby uniknąć tego problemu, funkcja oceny musi zwracać wartości będące dodatnią transformacją liniową prawdopodobieństwa wygranej (lub oczekiwanej użyteczności w przypadku gier, które mają wyniki inne niż wygrana/przegrana). Ten związek z prawdopodobieństwem jest ważną i ogólną właściwością sytuacji, w których występuje niepewność. Gdyby program znał z góry wszystkie rzuty kostką, które będą miały miejsce do końca gry, rozwiązanie gry kostkami byłoby jak rozwiązywanie gry bez kości, co robi minimaks w czasie O(bm), gdzie b jest rozgałęzieniem współczynnik, a m to maksymalna głębokość drzewa gry. Ponieważ expectiminimax uwzględnia również wszystkie możliwe sekwencje rzutów kostką, zajmie O(bm,nm) , gdzie n jest liczbą odrębnych rzutów. Nawet jeśli wyszukiwanie jest ograniczone do niewielkiej głębokości , dodatkowy koszt w porównaniu z minimaxem sprawia, że rozważanie patrzenia w przyszłość bardzo daleko w większości gier losowych jest nierealne. W tryktraku n wynosi 21 i zwykle wynosi około 20, ale w niektórych sytuacjach może wynosić nawet 4000 dla rzutów kośćmi, które są podwójne. Prawdopodobnie moglibyśmy przeprowadzić tylko trzy warstwy wyszukiwania. Inny sposób myślenia o problemie jest taki: zaletą alfa-bety jest to, że ignoruje przyszłe zmiany, które po prostu nie nastąpią, biorąc pod uwagę najlepszą grę. W związku z tym koncentruje się na prawdopodobnych zdarzeniach. Ale w grze, w której każdy ruch poprzedza rzut dwiema kośćmi, nie ma prawdopodobnych sekwencji ruchów; nawet najbardziej prawdopodobny ruch występuje tylko w połowie przypadków, ponieważ aby ruch mógł się odbyć, kostka musiałaby najpierw wypaść prawidłowo w sposób, aby było to legalne. Jest to ogólny problem, gdy pojawia się niepewność: możliwości są ogromnie mnożone, a szczegółowe planowanie działań staje się bezcelowe, bo świat prawdopodobnie nie będzie grał dalej. Być może przyszło ci do głowy, że coś takiego jak przycinanie alfa-beta można zastosować do drzew łownych z przypadkowymi węzłami. Okazuje się, że tak. Analiza węzłów MIN i MAX pozostaje niezmieniona, ale możemy również przycinać węzły przypadkowe, używając odrobiny pomysłowości. Rozważ węzeł szansy C na rysunku wcześniejszym i co dzieje się z jego wartością, gdy oceniamy jego dzieci. Czy można znaleźć górną granicę wartości C, zanim przyjrzymy się wszystkim jego dzieciom? (Przypomnij sobie, że właśnie tego potrzebuje alfa-beta, aby przyciąć węzeł i jego poddrzewo). Na pierwszy rzut oka może się to wydawać niemożliwe, ponieważ wartość C jest średnią wartości jego dzieci. A żeby obliczyć średnią ze zbioru liczb, musimy spojrzeć na wszystkie liczby. Ale jeśli umieścimy granice na możliwych wartościach funkcji użyteczności, wtedy możemy dojść do granic średniej bez patrzenia na każdą liczbę. Powiedzmy na przykład, że wszystkie wartości użyteczności mieszczą się w przedziale od -2 do +2 ; wtedy wartość węzłów liścia jest ograniczona, a z kolei możemy umieścić górną granicę na wartości węzła przypadkowego bez patrzenia na wszystkie jego dzieci. W grach, w których współczynnik rozgałęzień dla węzłów losowych jest wysoki, rozważ grę taką jak Yahtzee, w której rzucasz 5 kostkami w każdej turze – możesz rozważyć przycinanie do przodu, które próbkuje mniejszą liczbę możliwych rozgałęzień losowych. Możesz też całkowicie zrezygnować z funkcji oceny i zamiast tego wybrać wyszukiwanie drzewa Monte Carlo, gdzie każda rozgrywka obejmuje losowe rzuty kośćmi.