Gry stochastyczne przybliżają nas nieco do nieprzewidywalności prawdziwego życia, wprowadzając element losowy, taki jak rzucanie kostką. Backgammon to typowa gra stochastyczna, która łączy szczęście i umiejętności. W pozycji tryktraka z rysunku, białe wyrzuciły 6-5 i mają cztery możliwe ruchy (z których każdy porusza się jednym pionkiem do przodu (zgodnie z ruchem wskazówek zegara) o 5 pozycji, a jeden pionek do przodu o 6 pozycji).
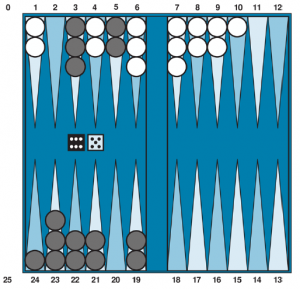
W tym momencie czarny wie, jakie ruchy mogą być wykonane, ale nie wie, co białe zamierzają wykonać, a zatem nie wie, jakie będą legalne ruchy białych. Oznacza to, że czarny nie może zbudować standardowego drzewa gry, takiego, jakie widzieliśmy w szachach i kółko i krzyżyk. Drzewo gry w tryktrak musi zawierać węzły losowe oprócz węzłów MAX i MIN. Przypadkowe węzły są pokazane jako koła na rysunku. Gałęzie prowadzące z każdego węzła losowego oznaczają możliwe rzuty kostką; każda gałąź jest oznaczona rolką i jej prawdopodobieństwem. Jest 36 sposobów rzucania dwiema kośćmi, każdy z równym prawdopodobieństwem; ale ponieważ 6-5 to to samo co 5-6, jest tylko 21 różnych rzutów. Każdy z sześciu dubli (1–1 do 6–6) ma prawdopodobieństwo 1/36, więc mówimy, że P(1-1) = 1/36 . Pozostałe 15 różnych rzutów ma prawdopodobieństwo 1/18.
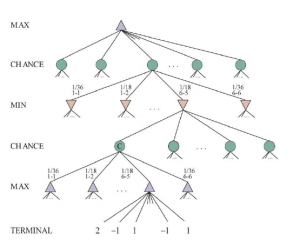
Następnym krokiem jest zrozumienie, jak podejmować właściwe decyzje. Oczywiście nadal chcemy wybrać ruch, który prowadzi do najlepszej pozycji. Jednak pozycje nie mają określonych wartości minimax. Zamiast tego możemy obliczyć tylko oczekiwaną wartość pozycji: średnią wszystkich możliwych wyników węzłów szansy. To prowadzi nas do wartości oczekiwanej minimaksowej dla gier z węzłami losowymi, uogólnienia wartości minimaksowej dla gier deterministycznych. Węzły końcowe oraz węzły MAX i MIN działają dokładnie tak samo jak poprzednio (z zastrzeżeniem, że prawidłowe ruchy dla MAX i MIN będą zależeć od wyniku rzutu kostką w poprzednim węźle szansy). Dla węzłów przypadkowych obliczamy wartość oczekiwaną, która jest sumą wartości wszystkich wyników, ważoną prawdopodobieństwem każdego działania przypadkowego:
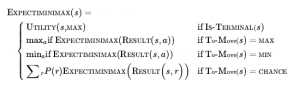
gdzie r reprezentuje możliwy rzut kostką (lub inne zdarzenie losowe), a RESULT(s,r) jest tym samym stanem co s , z dodatkowym faktem, że wynikiem rzutu jest r.