Skuteczność przycinania alfa-beta w dużym stopniu zależy od kolejności, w jakiej badane są stany. Na przykład na rysunku (e) i (f) nie mogliśmy w ogóle przyciąć żadnych następców D, ponieważ najgorsze następniki (z punktu widzenia MIN) zostały wygenerowane jako pierwsze.
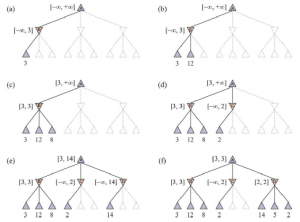
Gdyby trzeci następca D został wygenerowany jako pierwszy, z wartością 2, bylibyśmy w stanie przyciąć dwóch pozostałych następców. Sugeruje to, że warto spróbować najpierw zbadać następców, którzy prawdopodobnie będą najlepsi. Gdyby można było to zrobić perfekcyjnie, alfa-beta musiałaby zbadać tylko O(bm/2) węzły, aby wybrać najlepszy ruch, zamiast O(bm) dla minimaksu. Oznacza to, że efektywnym współczynnikiem rozgałęzienia staje się pierwiastek b zamiast b – dla szachów około 6 zamiast 35. Innymi słowy, alfa-beta z doskonałą kolejnością ruchów może rozwiązać drzewo mniej więcej dwa razy głębsze niż minimax w tym samym czasie . Przy losowej kolejności ruchów całkowita liczba zbadanych węzłów będzie w przybliżeniu wynosić O(b3m/4) dla umiarkowanego b . Teraz oczywiście nie możemy osiągnąć idealnego uporządkowania ruchów – w takim przypadku funkcja zamawiania mogłaby zostać wykorzystana do rozegrania doskonałej gry! Ale często możemy podejść dość blisko. W przypadku szachów dość prosta funkcja porządkowania (taka jak próba najpierw przechwytów, potem zagrożeń, potem ruchów do przodu, a następnie ruchów do tyłu) pozwala uzyskać mniej więcej czynnik 2 od wyniku w najlepszym przypadku O(bm/2).
Dodanie dynamicznych schematów kolejności ruchów, takich jak wypróbowywanie najpierw ruchów, które w przeszłości uznano za najlepsze, zbliża nas do teoretycznego limitu. Przeszłość może być poprzednim posunięciem – często pozostają te same zagrożenia – lub może pochodzić z wcześniejszej eksploracji obecnego posunięcia poprzez proces iteracyjnego pogłębiania. Najpierw przeszukaj jedną warstwę głęboko i zapisz ranking ruchów na podstawie ich ocen. Następnie przeszukaj jedną warstwę głębiej, używając poprzedniego rankingu do informowania o kolejności ruchów; i tak dalej. Wydłużony czas wyszukiwania wynikający z iteracyjnego pogłębiania może być więcej niż nadrobiony dzięki lepszemu porządkowaniu ruchów. Najlepsze ruchy są znane jako zabójcze ruchy, a wypróbowanie ich w pierwszej kolejności nazywa się heurystyką zabójczych ruchów.
Zauważyliśmy, że nadmiarowe ścieżki do powtarzających się stanów mogą powodować wykładniczy wzrost kosztów wyszukiwania, a prowadzenie tabeli stanów, które zostały wcześniej osiągnięte, może rozwiązać ten problem. W przeszukiwaniu drzewa gry mogą wystąpić powtarzające się stany z powodu transpozycji — różnych permutacji sekwencji ruchu, które kończą się w tej samej pozycji, a problem można rozwiązać za pomocą tabeli transpozycji, która buforuje wartości heurystyczne stanów. Załóżmy na przykład, że biały ma ruch w1, na który czarny może odpowiedzieć b1 i niepowiązany ruch w2 po drugiej stronie szachownicy, na który może odpowiedzieć b2 , i że przeszukujemy sekwencję ruchów [w1,b1,w2 ,b2 ] ; nazwijmy wynikowy stan . Po zbadaniu dużego poddrzewa poniżej znajdujemy jego kopię zapasową, którą przechowujemy w tabeli transpozycji. Kiedy później przeszukujemy sekwencję ruchów , znajdujemy się ponownie i możemy wyszukać wartość zamiast powtarzać wyszukiwanie. W szachach bardzo efektywne jest wykorzystanie tabel transpozycji, co pozwala nam podwoić osiągalną głębokość wyszukiwania w tym samym czasie. Nawet przy przycinaniu alfa-beta i sprytnym porządkowaniu ruchów minimax nie zadziała w grach takich jak szachy i Go, ponieważ wciąż jest zbyt wiele stanów do zbadania w dostępnym czasie. W pierwszym artykule na temat gier komputerowych, Programowanie komputera do gry w szachy, Claude Shannon rozpoznał ten problem i zaproponował dwie strategie: strategia typu A uwzględnia wszystkie możliwe ruchy do określonej głębokości w drzewie wyszukiwania, a następnie wykorzystuje heurystykę funkcja oceny do oszacowania użyteczności stanów na tej głębokości. Bada szeroką, ale płytką część drzewa. Strategia typu B ignoruje ruchy, które wyglądają źle i podąża za obiecującymi liniami „tak daleko, jak to możliwe”. Bada głęboką, ale wąską część drzewa. Historycznie, większość programów szachowych należała do Typu A (który omówimy w następnej sekcji), podczas gdy programy Go są częściej Typu B (omówione w Sekcji 5.4), ponieważ współczynnik rozgałęzienia jest znacznie wyższy w Go. Niedawno programy typu B pokazały grę na poziomie mistrzów świata w różnych grach, w tym w szachy