Liczba stanów gry jest wykładnicza na głębokości drzewa. Żaden algorytm nie jest w stanie całkowicie wyeliminować wykładnika, ale czasami możemy przeciąć go o połowę, obliczając prawidłową decyzję minimaksową bez badania każdego stanu poprzez przycinanie dużych części drzewa, które nie mają wpływu na wynik. Konkretna technika, którą badamy, nazywa się przycinaniem alfa-beta. Rozważmy ponownie dwuwarstwowe drzewo gry . Przejdźmy jeszcze raz przez obliczenie optymalnej decyzji, tym razem zwracając szczególną uwagę na to, co wiemy na każdym etapie procesu. Kroki są wyjaśnione na rysunku. Wynikiem jest to, że możemy zidentyfikować decyzję minimax bez oceny dwóch węzłów liści.
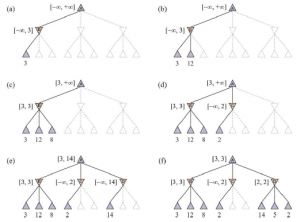
Innym sposobem spojrzenia na to jest uproszczenie formuły MINIMAX. Niech dwa nieocenione następniki węzła C na rysunku mają wartości x i y . Wtedy wartość węzła głównego jest dana przez

Innymi słowy, wartość pierwiastka, a tym samym decyzja o minimaksie, są niezależne od wartości liści x i y i dlatego można je przycinać. Przycinanie alfa-beta może być stosowane do drzew o dowolnej głębokości i często można przycinać całe poddrzewa, a nie tylko liście. Ogólna zasada jest następująca: rozważ węzeł n gdzieś w drzewie, taki, że Gracz ma wybór przejścia do . Jeśli Gracz ma lepszy wybór albo na tym samym poziomie (np. m’ na rysunku 5.6 ) lub w dowolnym punkcie wyżej w drzewie (np. m na rysunku), to nigdy nie przejdzie do . Więc kiedy już wystarczająco dowiedzieliśmy się o n (poprzez zbadanie niektórych jego potomków), aby dojść do tego wniosku, możemy je przyciąć.
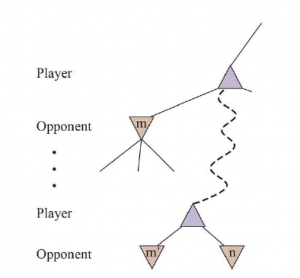
Pamiętaj, że wyszukiwanie minimaksowe jest na pierwszym miejscu, więc w dowolnym momencie musimy brać pod uwagę węzły wzdłuż pojedynczej ścieżki w drzewie. Przycinanie alfa-beta bierze swoją nazwę od dwóch dodatkowych parametrów w MAX-VALUE (stan α , β) , które opisują granice wartości kopii zapasowej, które pojawiają się w dowolnym miejscu na ścieżce:

α = wartość najlepszego (tj. najwyższej wartości) wyboru, jaki do tej pory znaleźliśmy w dowolnym punkcie wyboru na ścieżce dla MAX. Pomyśl: α = „przynajmniej”.
β = wartość najlepszego (tj. najniższej wartości) wyboru, jaki do tej pory znaleźliśmy w dowolnym punkcie wyboru na ścieżce dla MIN. Pomyśl: β = „co najwyżej”.
Wyszukiwanie alfa-beta aktualizuje wartości α i β w miarę postępu i usuwa pozostałe gałęzie w węźle (tj. kończy wywołanie rekurencyjne), gdy tylko wiadomo, że wartość bieżącego węzła jest gorsza niż bieżąca alfa lub wartość beta odpowiednio dla MAX lub MIN.