MAX chce znaleźć sekwencję działań prowadzących do wygranej, ale MIN ma na ten temat coś do powiedzenia. Oznacza to, że strategia MAX musi być planem warunkowym – strategią warunkową, określającą reakcję na każdy z możliwych ruchów MIN. W grach, które mają wynik binarny (wygrana lub przegrana), możemy użyć wyszukiwania AND–OR (strona 125), aby wygenerować plan warunkowy. W rzeczywistości w takich grach definicja strategii wygrywającej w grze jest identyczna z definicją rozwiązania niedeterministycznego problemu planowania: w obu przypadkach pożądany wynik musi być zagwarantowany bez względu na to, co zrobi „druga strona”. W przypadku gier z wieloma wynikami, potrzebujemy nieco bardziej ogólnego algorytmu zwanego wyszukiwaniem minimaksowym.
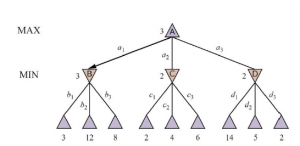
Rozważ trywialną grę z rysunku 5.2. Możliwe ruchy dla MAX w węźle głównym są oznaczone jako a1, a2 i a3. Możliwe odpowiedzi na a1 dla MIN to b1 , b2 , b3 i tak dalej. Ta konkretna gra kończy się po jednym ruchu, każdy o MAX i MIN. (UWAGA: W niektórych grach słowo „ruch” oznacza, że obaj gracze podjęli działanie; dlatego słowo ply jest używane do jednoznacznego oznaczenia jednego ruchu jednego gracza, co przenosi nas o jeden poziom głębiej w drzewo gry). stany terminali w tej grze wahają się od 2 do 14.
Mając dane drzewo gry, optymalną strategię można określić, wyliczając wartość minimaksową każdego stanu w drzewie, którą zapisujemy jako MINIMAX(y). Wartość minimax to użyteczność (dla MAX) bycia w tym stanie, przy założeniu, że obaj gracze grają optymalnie od tego momentu do końca gry. Wartość minimax stanu terminala to tylko jego użyteczność. W stanie nieterminalnym MAX woli przejść do stanu o maksymalnej wartości, gdy nadchodzi kolej MAXa na ruch, a MIN preferuje stan o minimalnej wartości (czyli minimalnej wartości dla MAX, a tym samym maksymalnej wartości dla MIN). Więc mamy:
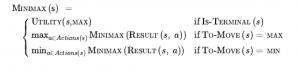
Zastosujmy te definicje do drzewa gry na rysunku 5.2. Węzły końcowe na dolnym poziomie uzyskują swoje wartości użytkowe z funkcji UTILITY w grze. Pierwszy węzeł MIN, oznaczony etykietą , ma trzy stany następcze o wartościach 3, 12 i 8, więc jego wartość minimax wynosi 3. Podobnie pozostałe dwa węzły MIN mają wartość minimax 2. Węzeł główny jest węzłem MAX; jego stany następcze mają wartości minimax 3, 2 i 2; więc ma wartość minimaksową równą 3. Możemy również zidentyfikować decyzję minimaksową u korzenia: akcja a1 jest optymalnym wyborem dla MAX, ponieważ prowadzi do stanu o najwyższej wartości minimaksowej.
Ta definicja optymalnej gry dla MAX zakłada, że MIN również gra optymalnie. Co jeśli MIN nie gra optymalnie? Wtedy MAX poradzi sobie co najmniej tak dobrze, jak przeciwko optymalnemu graczowi, a może nawet lepiej. Nie oznacza to jednak, że zawsze najlepiej jest zagrać optymalny ruch minimaksowy w obliczu nieoptymalnego przeciwnika. Rozważ sytuację, w której optymalna gra obu stron doprowadzi do remisu, ale jest jeden ryzykowny ruch dla MAX, który prowadzi do stanu, w którym jest 10 możliwych ruchów odpowiedzi na MIN, które wydają się rozsądne, ale 9 z nich to strata dla MIN, a jeden to strata dla MAX. Jeśli MAX uważa, że MIN nie ma wystarczającej mocy obliczeniowej, aby odkryć optymalny ruch, MAX może chcieć spróbować ryzykownego ruchu, ponieważ szansa 9/10 na wygraną jest lepsza niż pewien remis.