Gry najczęściej badane w ramach sztucznej inteligencji (takie jak szachy i go) to gry, które teoretycy gier nazywają deterministycznymi, dwuosobowymi, rozgrywającymi się na zmianę, z doskonałą informacją, grami o sumie zerowej. „Doskonała informacja” jest synonimem „w pełni obserwowalnej”, a „suma zerowa” oznacza, że to, co jest dobre dla jednego gracza, jest tak samo złe dla drugiego: nie ma wyniku „wygrana-wygrana”. W grach często używamy terminu move jako synonimu „akcji” i pozycji jako synonimu „stanu”. Zadzwonimy do naszych dwóch graczy MAX i MIN, z powodów, które wkrótce staną się oczywiste. MAX porusza się jako pierwszy, a następnie gracze na zmianę poruszają się, aż gra się skończy. Na koniec gry zwycięski gracz otrzymuje punkty, a przegrany otrzymuje kary. Gra może być formalnie zdefiniowana za pomocą następujących elementów:
* S0 : Stan początkowy, który określa, jak gra jest skonfigurowana na początku.
* TO-MOVE(s): Gracz, którego kolej ma się poruszyć w stanie .
* ACTIONS : Zestaw prawidłowych ruchów w stanie .
* RESULTS(s,a): Model przejścia, który definiuje stan wynikający z podjęcia działań w stanie .
* IS-TERMINAL(s): Test terminala, który jest prawdziwy po zakończeniu gry i fałszywy w przeciwnym razie. Stany, w których gra się zakończyła, nazywane są stanami końcowymi.
* UTILITY(s,p) : Funkcja użyteczności (nazywana również funkcją celu lub funkcją wypłaty), która definiuje ostateczną wartość liczbową dla gracza, gdy gra kończy się w stanie terminala. W szachach wynikiem jest wygrana, przegrana lub remis z wartościami 1 , 0 lub 1/2 . Niektóre gry mają szerszy zakres możliwych wyników – na przykład wypłaty w tryktraku wahają się od 0 do 192 .
Podobnie jak wcześniej , stan początkowy, funkcja AKCJE i funkcja WYNIK definiują graf przestrzeni stanów – graf, w którym wierzchołki są stanami, krawędziami są ruchami, a stan może być osiągnięty wieloma ścieżkami. Możemy nałożyć drzewo poszukiwań na część tego wykresu, aby określić, jaki ruch wykonać. Kompletne drzewo gry definiujemy jako drzewo wyszukiwania, które podąża za każdą sekwencją ruchów aż do stanu terminala. Drzewo gry może być nieskończone, jeśli sama przestrzeń stanów jest nieograniczona lub jeśli reguły gry pozwalają na nieskończenie powtarzające się pozycje. Rysunek przedstawia część drzewa gry w kółko i krzyżyk (kółko i krzyżyk). Od stanu początkowego MAX ma dziewięć możliwych ruchów. Gra naprzemiennie polega na tym, że MAX umieszcza X MIN, umieszcza O, aż dotrzemy do węzłów liści odpowiadających stanom końcowym, tak że jeden gracz ma trzy kwadraty z rzędu lub wszystkie kwadraty są wypełnione. Liczba na każdym węźle liścia wskazuje wartość użytkową stanu końcowego z punktu widzenia MAX; wysokie wartości są dobre dla MAX, a złe dla MIN (w ten sposób gracze otrzymują swoje nazwy).
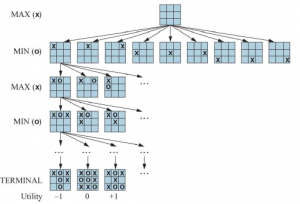
W przypadku gry w kółko i krzyżyk drzewo gry jest stosunkowo mniejsze niż 9! = 362 880 węzłów końcowych (tylko 5478 różnych stanów). Ale w szachach istnieją ponad węzły, więc drzewo gry najlepiej traktować jako konstrukt teoretyczny, którego nie możemy zrealizować w świecie fizycznym.