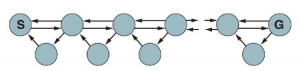
Podobnie jak wyszukiwanie w głąb, wyszukiwanie ze wspinaczką ma właściwość lokalizacji w rozwinięciach węzłów. W rzeczywistości, ponieważ przechowuje tylko jeden aktualny stan w pamięci, wyszukiwanie wspinaczkowe jest już algorytmem wyszukiwania online! Niestety podstawowy algorytm nie jest zbyt dobry do eksploracji, ponieważ pozostawia agenta siedzącego na lokalnych maksimach bez miejsca, do którego mógłby się udać. Ponadto nie można używać losowych restartów, ponieważ agent nie może teleportować się do nowego stanu startowego. Zamiast losowych restartów, można rozważyć skorzystanie z przypadkowego spaceru w celu zbadania otoczenia. Spacer losowy po prostu wybiera losowo jedną z dostępnych akcji z bieżącego stanu; pierwszeństwo mogą mieć działania, które nie zostały jeszcze wypróbowane. Łatwo jest udowodnić, że losowy spacer w końcu znajdzie cel lub dokończy jego eksplorację, pod warunkiem, że przestrzeń jest skończona i bezpieczna do eksploracji. Z drugiej strony proces może być bardzo powolny. Rysunek pokazuje środowisko, w którym błądzenie losowe wymaga wykładniczo wielu kroków, aby znaleźć cel, ponieważ dla każdego stanu w górnym wierszu z wyjątkiem S, postęp wstecz jest dwa razy bardziej prawdopodobny niż postęp w przód. Przykład jest oczywiście wymyślony, ale istnieje wiele rzeczywistych przestrzeni stanów, których topologia powoduje tego rodzaju „pułapki” na losowe spacery.
Wspinanie się po wzgórzach za pomocą pamięci, a nie przypadkowości, okazuje się bardziej skutecznym podejściem. Podstawowym pomysłem jest przechowywanie „aktualnego najlepszego oszacowania” H(ów) kosztów, aby osiągnąć cel z każdego odwiedzonego stanu. H(s) zaczyna być tylko oszacowaniem heurystycznym h(s) i jest aktualizowane, gdy agent zdobywa doświadczenie w przestrzeni stanów. Rysunek pokazuje prosty przykład w jednowymiarowej przestrzeni stanów. W (a) agent wydaje się utknąć w płaskim lokalnym minimum w stanie czerwonym. Zamiast pozostawać tam, gdzie jest, agent powinien podążać drogą, która wydaje się być najlepszą ścieżką do celu, biorąc pod uwagę aktualne szacunki kosztów dla sąsiadów. Szacowany koszt dotarcia do celu przez sąsiada s’ to koszt dotarcia do s’ plus szacowany koszt dotarcia do celu stamtąd, czyli .c(s,a,s’) + H(s’ ) . W tym przykładzie są dwie akcje, z szacowanymi kosztami po lewej i po prawej stronie, więc wydaje się, że najlepiej przejść w prawo.
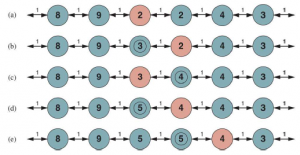
W punkcie (b) wyraźnie widać, że szacunek kosztów 2 dla stanu czerwonego w punkcie (a) był zbyt optymistyczny. Ponieważ najlepszy ruch kosztował 1 i doprowadził do stanu, który jest co najmniej 2 kroki od celu, czerwony stan musi znajdować się co najmniej 3 kroki od celu, więc jego H należy odpowiednio zaktualizować, jak pokazano na rysunku (b). . Kontynuując ten proces, agent będzie się jeszcze dwa razy poruszał tam i z powrotem, za każdym razem aktualizując H i „spłaszczając” lokalne minimum, aż ucieknie w prawo.
Agenta realizującego ten schemat, który nazywa się uczeniem się A* w czasie rzeczywistym (LRTA*), pokazano na rysunku. Podobnie jak ONLINE-DFS-AGENT, buduje mapę środowiska w tabeli wyników. Aktualizuje oszacowanie kosztów dla stanu, który właśnie opuścił, a następnie wybiera „najwyraźniej najlepszy” ruch zgodnie z aktualnymi szacunkami kosztów. Ważnym szczegółem jest to, że zakłada się, że działania, które nie zostały jeszcze wypróbowane w danym stanie, prowadzą natychmiast do celu przy możliwie najmniejszych kosztach, czyli h(s). Ten optymizm w warunkach niepewności skłania agenta do poszukiwania nowych, potencjalnie obiecujących ścieżek.

Agent LRTA* gwarantuje znalezienie celu w każdym ograniczonym, bezpiecznym środowisku. Jednak w przeciwieństwie do A*, nie jest ona zupełna dla nieskończonych przestrzeni stanów — są przypadki, w których może być wyprowadzona na nieskończenie błąd. W najgorszym przypadku może badać środowisko składające się z n stanów w krokach O(n2), ale często działa znacznie lepiej. Agent LRTA* jest tylko jednym z dużej rodziny agentów online, które można zdefiniować, określając na różne sposoby regułę wyboru akcji i regułę aktualizacji. Omawiamy tę rodzinę, opracowaną pierwotnie dla środowisk stochastycznych