Świat próżni ma osiem stanów, jak pokazano na rysunku
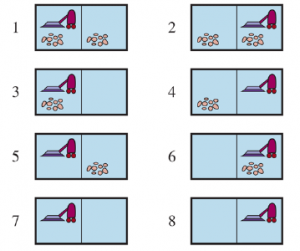
Istnieją trzy akcje — Prawo, Lewo i Ssanie — a celem jest oczyszczenie całego brudu (stany 7 i 8). Jeśli środowisko jest w pełni obserwowalne, deterministyczne i całkowicie znane, to problem można łatwo rozwiązać dowolnym algorytmem z rozdziału 3, a rozwiązaniem jest sekwencja działań. Na przykład, jeśli stan początkowy wynosi 1, to sekwencja działań [Ssanie, Prawo, Ssanie] osiągnie stan docelowy 8.
Załóżmy teraz, że wprowadzamy niedeterminizm w postaci potężnego, ale nieobliczalnego odkurzacza. W nieobliczalnym świecie próżni akcja Ssania działa w następujący sposób:
*Po nałożeniu na brudny kwadrat, działanie czyści kwadrat, a czasem usuwa również brud z sąsiedniego kwadratu.
* Po nałożeniu na czysty kwadrat, działanie czasami powoduje osadzanie brudu na dywanie.
Aby precyzyjnie sformułować ten problem, musimy uogólnić pojęcie modelu przejścia z rozdziału 3 . Zamiast definiować model przejścia przez funkcję WYNIK, która zwraca pojedynczy stan wyniku, używamy funkcji WYNIKI, która zwraca zestaw możliwych stanów wyniku. Na przykład w świecie błędnej próżni akcja Suck w stanie 1 czyści albo tylko bieżącą lokalizację, albo obie lokalizacje:
RESULTS(1, Suck) = {5,7}
Jeśli zaczniemy w stanie 1, żadna pojedyncza sekwencja działań nie rozwiąże problemu, ale następujący plan warunkowy tak:
[Suck, if State = 5 to [Right, Suck] else [ ]] .
Widzimy tutaj, że plan warunkowy może zawierać kroki „jeśli-to-inne”; oznacza to, że rozwiązania są drzewami, a nie sekwencjami. Tutaj warunek w instrukcji if sprawdza, jaki jest aktualny stan; jest to coś, co agent będzie mógł obserwować w czasie wykonywania, ale nie wie w czasie planowania. Alternatywnie moglibyśmy mieć sformułowanie testujące raczej percepcję niż stan. Wiele problemów w rzeczywistym, fizycznym świecie to problemy przypadkowe, ponieważ dokładne przewidzenie przyszłości jest niemożliwe. Z tego powodu wiele osób ma otwarte oczy podczas chodzenia.