Miesiąc: wrzesień 2021

Podobnie jak w przypadku minimaxu, oczywistym przybliżeniem, jakie można zrobić z expectiminimaxem, jest odcięcie wyszukiwania w pewnym momencie i zastosowanie funkcji oceny do każdego liścia. Można by pomyśleć, że funkcje ewaluacyjne w grach takich jak tryktrak powinny być takie same jak funkcje ewaluacyjne w szachach – po prostu muszą dawać wyższe wartości lepszym pozycjom. Ale w rzeczywistości obecność przypadkowych węzłów oznacza, że trzeba być bardziej ostrożnym, co oznaczają wartości.

Rysunek  pokazuje, co się dzieje: z funkcją oceny, która przypisuje wartości [1, 2, 3, 4] do liści, ruch a₁ jest najlepszy; o wartościach [1, 20, 30, 400] najlepiej jest wykonać ruch a₂. W związku z tym program zachowuje się zupełnie inaczej, jeśli dokonamy zmiany niektórych wartości oceny, nawet jeśli kolejność preferencji pozostaje taka sama.

Okazuje się, że aby uniknąć tego problemu, funkcja oceny musi zwracać wartości będące dodatnią transformacją liniową prawdopodobieństwa wygranej (lub oczekiwanej użyteczności w przypadku gier, które mają wyniki inne niż wygrana/przegrana). Ten związek z prawdopodobieństwem jest ważną i ogólną właściwością sytuacji, w których występuje niepewność. Gdyby program znał z góry wszystkie rzuty kostką, które będą miały miejsce do końca gry, rozwiązanie gry kostkami byłoby jak rozwiązywanie gry bez kości, co robi minimaks w czasie O(b^m), gdzie b jest rozgałęzieniem współczynnik, a m to maksymalna głębokość drzewa gry. Ponieważ expectiminimax uwzględnia również wszystkie możliwe sekwencje rzutów kostką, zajmie O(b^m,n^m) , gdzie n jest liczbą odrębnych rzutów. Nawet jeśli wyszukiwanie jest ograniczone do niewielkiej głębokości , dodatkowy koszt w porównaniu z minimaxem sprawia, że ​​rozważanie patrzenia w przyszłość bardzo daleko w większości gier losowych jest nierealne. W tryktraku n wynosi 21 i zwykle wynosi około 20, ale w niektórych sytuacjach może wynosić nawet 4000 dla rzutów kośćmi, które są podwójne. Prawdopodobnie moglibyśmy przeprowadzić tylko trzy warstwy wyszukiwania. Inny sposób myślenia o problemie jest taki: zaletą alfa-bety jest to, że ignoruje przyszłe zmiany, które po prostu nie nastąpią, biorąc pod uwagę najlepszą grę. W związku z tym koncentruje się na prawdopodobnych zdarzeniach. Ale w grze, w której każdy ruch poprzedza rzut dwiema kośćmi, nie ma prawdopodobnych sekwencji ruchów; nawet najbardziej prawdopodobny ruch występuje tylko w połowie przypadków, ponieważ aby ruch mógł się odbyć, kostka musiałaby najpierw wypaść prawidłowo w sposób, aby było to legalne. Jest to ogólny problem, gdy pojawia się niepewność: możliwości są ogromnie mnożone, a szczegółowe planowanie działań staje się bezcelowe, bo świat prawdopodobnie nie będzie grał dalej. Być może przyszło ci do głowy, że coś takiego jak przycinanie alfa-beta można zastosować do drzew łownych z przypadkowymi węzłami. Okazuje się, że tak. Analiza węzłów MIN i MAX pozostaje niezmieniona, ale możemy również przycinać węzły przypadkowe, używając odrobiny pomysłowości. Rozważ węzeł szansy C na rysunku wcześniejszym i co dzieje się z jego wartością, gdy oceniamy jego dzieci. Czy można znaleźć górną granicę wartości C, zanim przyjrzymy się wszystkim jego dzieciom? (Przypomnij sobie, że właśnie tego potrzebuje alfa-beta, aby przyciąć węzeł i jego poddrzewo). Na pierwszy rzut oka może się to wydawać niemożliwe, ponieważ wartość C jest średnią wartości jego dzieci. A żeby obliczyć średnią ze zbioru liczb, musimy spojrzeć na wszystkie liczby. Ale jeśli umieścimy granice na możliwych wartościach funkcji użyteczności, wtedy możemy dojść do granic średniej bez patrzenia na każdą liczbę. Powiedzmy na przykład, że wszystkie wartości użyteczności mieszczą się w przedziale od -2 do +2 ; wtedy wartość węzłów liścia jest ograniczona, a z kolei możemy umieścić górną granicę na wartości węzła przypadkowego bez patrzenia na wszystkie jego dzieci. W grach, w których współczynnik rozgałęzień dla węzłów losowych jest wysoki, rozważ grę taką jak Yahtzee, w której rzucasz 5 kostkami w każdej turze – możesz rozważyć przycinanie do przodu, które próbkuje mniejszą liczbę możliwych rozgałęzień losowych. Możesz też całkowicie zrezygnować z funkcji oceny i zamiast tego wybrać wyszukiwanie drzewa Monte Carlo, gdzie każda rozgrywka obejmuje losowe rzuty kośćmi.

Gry stochastyczne przybliżają nas nieco do nieprzewidywalności prawdziwego życia, wprowadzając element losowy, taki jak rzucanie kostką. Backgammon to typowa gra stochastyczna, która łączy szczęście i umiejętności. W pozycji tryktraka z rysunku, białe wyrzuciły 6-5 i mają cztery możliwe ruchy (z których każdy porusza się jednym pionkiem do przodu (zgodnie z ruchem wskazówek zegara) o 5 pozycji, a jeden pionek do przodu o 6 pozycji).

W tym momencie czarny wie, jakie ruchy mogą być wykonane, ale nie wie, co białe zamierzają wykonać, a zatem nie wie, jakie będą legalne ruchy białych. Oznacza to, że czarny nie może zbudować standardowego drzewa gry, takiego, jakie widzieliśmy w szachach i kółko i krzyżyk. Drzewo gry w tryktrak musi zawierać węzły losowe oprócz węzłów MAX i MIN. Przypadkowe węzły są pokazane jako koła na rysunku. Gałęzie prowadzące z każdego węzła losowego oznaczają możliwe rzuty kostką; każda gałąź jest oznaczona rolką i jej prawdopodobieństwem. Jest 36 sposobów rzucania dwiema kośćmi, każdy z równym prawdopodobieństwem; ale ponieważ 6-5 to to samo co 5-6, jest tylko 21 różnych rzutów. Każdy z sześciu dubli (1–1 do 6–6) ma prawdopodobieństwo 1/36, więc mówimy, że P(1-1) = 1/36 . Pozostałe 15 różnych rzutów ma prawdopodobieństwo 1/18.

Następnym krokiem jest zrozumienie, jak podejmować właściwe decyzje. Oczywiście nadal chcemy wybrać ruch, który prowadzi do najlepszej pozycji. Jednak pozycje nie mają określonych wartości minimax. Zamiast tego możemy obliczyć tylko oczekiwaną wartość pozycji: średnią wszystkich możliwych wyników węzłów szansy. To prowadzi nas do wartości oczekiwanej minimaksowej dla gier z węzłami losowymi, uogólnienia wartości minimaksowej dla gier deterministycznych. Węzły końcowe oraz węzły MAX i MIN działają dokładnie tak samo jak poprzednio (z zastrzeżeniem, że prawidłowe ruchy dla MAX i MIN będą zależeć od wyniku rzutu kostką w poprzednim węźle szansy). Dla węzłów przypadkowych obliczamy wartość oczekiwaną, która jest sumą wartości wszystkich wyników, ważoną prawdopodobieństwem każdego działania przypadkowego:

gdzie  r reprezentuje możliwy rzut kostką (lub inne zdarzenie losowe), a RESULT(s,r) jest tym samym stanem co s , z dodatkowym faktem, że wynikiem rzutu jest r.

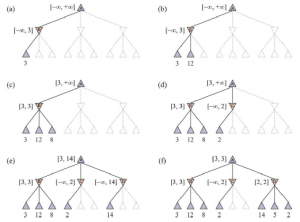
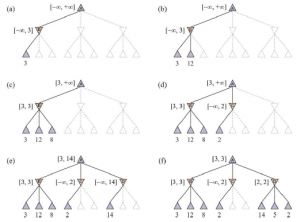
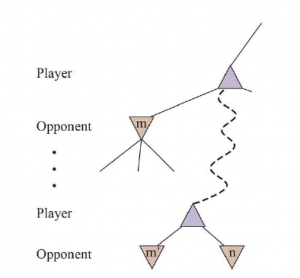
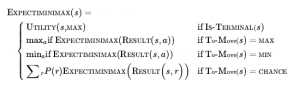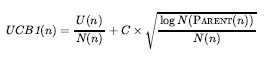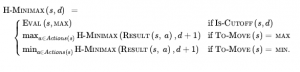Gra w Go ilustruje dwie główne słabości wyszukiwania heurystycznego w drzewie alfa-beta: Po pierwsze, Go ma współczynnik rozgałęzienia, który zaczyna się od 361, co oznacza, że ​​wyszukiwanie w alfabecie alfa będzie ograniczone tylko do 4 lub 5 warstw. Po drugie, trudno jest zdefiniować dobrą funkcję oceny dla Go, ponieważ wartość materialna nie jest silnym wskaźnikiem, a większość pozycji zmienia się aż do końca gry. W odpowiedzi na te dwa wyzwania, współczesne programy Go zrezygnowały z wyszukiwania alfa-beta i zamiast tego używają strategii zwanej przeszukiwaniem drzewa Monte Carlo (MCTS). Podstawowa strategia MCTS nie wykorzystuje funkcji oceny heurystycznej. Zamiast tego wartość stanu jest szacowana jako średnia użyteczność w wielu symulacjach pełnych gier, zaczynając od stanu. Symulacja (zwana również playout lub rollout) wybiera ruchy najpierw dla jednego gracza, a następnie dla drugiego, powtarzając aż do osiągnięcia końcowej pozycji. W tym momencie reguły gry (nie omylna heurystyka) określają, kto wygrał lub przegrał, i jaki jest wynik. W przypadku gier, w których jedynymi wynikami są wygrana lub przegrana, „średnia użyteczność” jest taka sama, jak „procent wygranych”. Jak wybieramy ruchy do wykonania podczas rozgrywki? Jeśli wybieramy po prostu losowo, to po wielu symulacjach otrzymujemy odpowiedź na pytanie „jaki jest najlepszy ruch, jeśli obaj gracze grają losowo?” W przypadku niektórych prostych gier jest to ta sama odpowiedź, co „jaki jest najlepszy ruch, jeśli obaj gracze grają dobrze?”, ale w większości gier tak nie jest. Aby uzyskać przydatne informacje z rozgrywek, potrzebujemy polityki rozgrywek, która skłania ruchy do dobrych. W przypadku Go i innych gier zasady dotyczące odtwarzania zostały z powodzeniem nauczone podczas samodzielnej gry przy użyciu sieci neuronowych. Czasami używane są heurystyki specyficzne dla gry, takie jak „rozważ ruchy bicia” w szachach lub „zajmij kwadrat narożny” w Othello. Biorąc pod uwagę zasady dotyczące rozgrywania, musimy następnie zdecydować o dwóch rzeczach: od jakich pozycji rozpoczynamy playouty i ile playoutów przydzielimy do każdej pozycji? Najprostszą odpowiedzią, nazywaną czystym wyszukiwaniem Monte Carlo, jest wykonanie N symulacji, zaczynając od aktualnego stanu gry i śledzenie, który z możliwych ruchów z aktualnej pozycji ma najwyższy procent wygranych. W przypadku niektórych gier stochastycznych to zbiega się do optymalnej rozgrywki wraz ze wzrostem liczby N, ale w przypadku większości gier jest to niewystarczające — potrzebujemy polityki selekcji, która selektywnie skupia zasoby obliczeniowe na ważnych częściach drzewa gry. Równoważy dwa czynniki: eksplorację stanów, które miały niewiele playoutów, oraz eksploatację stanów, które radziły sobie dobrze w poprzednich playoutach, aby uzyskać dokładniejsze oszacowanie ich wartości. Wyszukiwanie drzewa metodą Monte Carlo robi to, utrzymując drzewo wyszukiwania i rozwijając je w każdej iteracji następujących czterech kroków

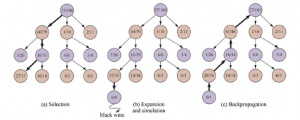
SELEKCJA: Zaczynając od korzenia drzewa wyszukiwania, wybieramy ruch (kierując się polityką selekcji), prowadzący do węzła następnika i powtarzamy ten proces, przechodząc w dół drzewa do liścia. Rysunek 5.10(a) pokazuje drzewo wyszukiwania z korzeniem reprezentującym stan, w którym biały właśnie się przeniósł, a biały wygrał 37 ze 100 rozegranych do tej pory. Gruba strzałka pokazuje wybór ruchu przez czarne, który prowadzi do węzła, w którym czarne wygrały 60/79 playoutów. Jest to najlepszy procent wygranych spośród trzech ruchów, więc wybranie go jest przykładem wyzysku. Ale rozsądne byłoby również wybranie węzła 2/11 ze względu na eksplorację – mając tylko 11 playoutów, węzeł nadal ma dużą niepewność w swojej wycenie i może okazać się najlepszy, jeśli zdobędziemy więcej informacji na jego temat. Zaznaczanie jest kontynuowane do węzła liścia oznaczonego 27/35.

ROZSZERZENIE: Rozwijamy drzewo wyszukiwania, generując nowe dziecko wybranego węzła; Rysunek (b) przedstawia nowy węzeł oznaczony cyfrą 0/0. (Niektóre wersje generują w tym kroku więcej niż jedno dziecko).

SYMULACJA: Wykonujemy playout z nowo wygenerowanego węzła podrzędnego, wybierając ruchy dla obu graczy zgodnie z polityką playout. Te ruchy nie są rejestrowane w drzewie wyszukiwania. Na rysunku symulacja skutkuje wygraną czarnych.

PROPAGACJA WSTECZNA: Używamy teraz wyniku symulacji, aby zaktualizować wszystkie węzły drzewa wyszukiwania, aż do korzenia. Ponieważ czarny wygrał rozgrywkę, czarne węzły są zwiększane zarówno pod względem liczby wygranych, jak i liczby playoutów, więc 27/35 staje się 28/26, a 60/79 staje się 61/80. Ponieważ białe węzły zostały utracone, liczba białych węzłów zwiększa się tylko pod względem liczby odtworzeń, więc 16/53 staje się 16/54, a pierwiastek 37/100 staje się 37/101.

Powtarzamy te cztery kroki albo przez określoną liczbę iteracji, albo do upłynięcia wyznaczonego czasu, a następnie zwracamy ruch z największą liczbą odtworzeń. Jedna bardzo skuteczna polityka selekcji nazywa się „górnymi granicami ufności stosowanymi do drzew” lub UCT. Polityka klasyfikuje każdy możliwy ruch w oparciu o formułę górnej granicy ufności o nazwie UCB1. Dla węzła n wzór jest następujący:

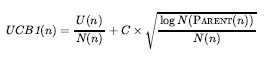
gdzie to całkowita użyteczność wszystkich playoutów, które przeszły przez węzeł n, N(n) to liczba playoutów przez węzeł n , a PARENT(n) to węzeł nadrzędny n w drzewie. Zatem U(n)/N(n) jest terminem eksploatacyjnym: średnia użyteczność . Termin z pierwiastkiem kwadratowym to termin eksploracji: ma liczbę N(n) w mianowniku, co oznacza, że ​​termin będzie wysoki dla węzłów, które zostały zbadane tylko kilka razy. W liczniku znajduje się dziennik, ile razy badaliśmy rodzica . Oznacza to, że jeśli wybieramy n jakiś niezerowy procent czasu, termin eksploracji schodzi do zera wraz ze wzrostem liczebności, a ostatecznie odtworzenia są przekazywane do węzła o najwyższej średniej użyteczności. C jest stałą, która równoważy eksploatację i eksplorację. Istnieje teoretyczny argument, że C powinien być piewisatek z 2 , ale w praktyce programiści gier próbują wielu wartości dla C i wybierają tę, która działa najlepiej. (Niektóre programy używają nieco innych wzorów; na przykład ALPHAZERO dodaje termin określający prawdopodobieństwo ruchu, który jest obliczany przez sieć neuronową wytrenowaną na podstawie wcześniejszej samoodgrywania.) Przy C=1,4 węzeł 60/79 na rysunku powyżej ma najwyższy wynik UCB1, ale przy C=1.5 byłby to węzeł 2/11.

Poniższy rysunek przedstawia kompletny algorytm UCT MCTS. Po zakończeniu iteracji ruch z największą liczbą odtworzeń zostaje zwrócony. Możesz pomyśleć, że lepiej byłoby zwrócić węzeł z najwyższą średnią użytecznością, ale pomysł jest taki, że węzeł z wygranymi 65/100 jest lepszy niż ten z wygranymi 2/3, ponieważ ten drugi ma dużą niepewność. W każdym razie formuła UCB1 zapewnia, że ​​węzeł z największą liczbą playoutów jest prawie zawsze węzłem z najwyższym procentem wygranych, ponieważ proces selekcji coraz bardziej faworyzuje procent wygranych wraz ze wzrostem liczby playoutów.

Czas na obliczenie rozgrywek jest liniowy, a nie wykładniczy, w głębi drzewa gry, ponieważ w każdym punkcie wyboru wykonywany jest tylko jeden ruch. To daje nam mnóstwo czasu na wiele rozgrywek. Na przykład: rozważ grę ze współczynnikiem rozgałęzienia 32, gdzie

średnia gra trwa 100 warstw. Jeśli mamy wystarczającą moc obliczeniową, aby rozważyć miliard stanów gry, zanim będziemy musieli wykonać ruch, to minimax może przeszukiwać 6 warstw, alfa-beta z doskonałym porządkowaniem ruchów może przeszukiwać 12 warstw, a wyszukiwanie Monte Carlo może wykonać 10 milionów odtworzeń. Które podejście będzie lepsze? Zależy to od dokładności funkcji heurystycznej w porównaniu z zasadami wyboru i odtwarzania. Powszechnie uważa się, że wyszukiwanie metodą Monte Carlo ma przewagę nad alfa-betą w grach takich jak Go, w których współczynnik rozgałęzienia jest bardzo wysoki (a zatem alfa-beta nie może wyszukiwać wystarczająco głęboko) lub gdy trudno jest zdefiniować dobry funkcja oceny. To, co robi alfa-beta, to wybór ścieżki do węzła, który ma najwyższy osiągalny wynik funkcji oceny, biorąc pod uwagę, że przeciwnik będzie próbował zminimalizować wynik. Tak więc, jeśli funkcja oceny jest niedokładna, alfa-beta będzie niedokładna. Błędne obliczenia na pojedynczym węźle mogą spowodować, że alfa-beta błędnie wybierze (lub ominie) ścieżkę do tego węzła. Ale wyszukiwanie Monte Carlo opiera się na agregacie wielu playoutów, a zatem nie jest tak podatne na pojedynczy błąd. Możliwe jest połączenie MCTS i funkcji oceny, wykonując playout dla określonej liczby ruchów, a następnie skracając playout i stosując funkcję oceny. Możliwe jest również połączenie aspektów wyszukiwania alfa-beta i Monte Carlo. Na przykład w grach, które mogą trwać wiele ruchów, możemy chcieć użyć wczesnego zakończenia gry, w którym zatrzymujemy grę, która zajmuje zbyt wiele ruchów i albo oceniamy ją za pomocą funkcji oceny heurystycznej, albo po prostu ogłaszamy remis.

Wyszukiwanie metodą Monte Carlo można zastosować do zupełnie nowych gier, w których nie ma żadnego doświadczenia, z którego można by czerpać, aby zdefiniować funkcję oceny. Dopóki znamy zasady gry, wyszukiwanie w Monte Carlo nie wymaga żadnych dodatkowych informacji. Zasady selekcji i odtwarzania mogą dobrze wykorzystać zdobytą ręcznie wiedzę ekspercką, gdy jest ona dostępna, ale dobrych zasad można się nauczyć, korzystając z sieci neuronowych wyszkolonych wyłącznie przez samodzielną grę. Wyszukiwanie Monte Carlo ma wadę, gdy jest prawdopodobne, że pojedynczy ruch może zmienić przebieg gry, ponieważ stochastyczny charakter wyszukiwania Monte Carlo oznacza, że ​​może nie wziąć pod uwagę tego ruchu. Innymi słowy, przycinanie typu B w wyszukiwaniu Monte Carlo oznacza, że ​​kluczowa linia gry może w ogóle nie zostać zbadana. Wyszukiwanie Monte Carlo ma również wadę, gdy istnieją stany gry, które są „oczywiście” wygraną dla jednej lub drugiej strony (zgodnie z ludzką wiedzą i funkcją oceny), ale w przypadku, gdy weryfikacja wymaga wielu ruchów w playout Zwycięzca. Od dawna utrzymywano, że wyszukiwanie alfa-beta lepiej nadaje się do gier takich jak szachy z niskim współczynnikiem rozgałęzienia i dobrymi funkcjami oceny, ale ostatnio podejście Monte Carlo wykazało sukces w szachach i innych grach. Ogólna idea symulowania ruchów w przyszłość, obserwowanie wyniku i wykorzystywanie wyniku do określenia, które ruchy są dobre, jest jednym z rodzajów uczenia się przez wzmacnianie

Wydaje się, że to przesadą, aby program szachowy rozpoczynał partię, biorąc pod uwagę drzewo składające się z miliarda stanów gry, tylko po to, by dojść do wniosku, że będzie grał pionkiem do e4 (najpopularniejszy pierwszy ruch). Książki opisujące dobrą grę w debiucie i końcówce szachów są dostępne od ponad wieku. Nie jest zatem zaskakujące, że wiele programów do grania w gry używa wyszukiwania tabel zamiast wyszukiwania początku i końca gier. W przypadku otworów komputer opiera się głównie na wiedzy ludzi. Najlepsze rady ludzkich ekspertów na temat tego, jak grać w każdy debiut, można skopiować z książek i umieścić w tabelach na użytek komputera. Ponadto komputery mogą gromadzić statystyki z bazy danych rozegranych wcześniej gier, aby zobaczyć, które sekwencje otwarcia najczęściej prowadzą do wygranej. Dla pierwszych kilku ruchów jest kilka możliwości, a większość pozycji będzie w tabeli. Zwykle po około 10 lub 15 ruchach znajdujemy się w rzadko spotykanej pozycji, a program musi przełączyć się z wyszukiwania tabeli na wyszukiwanie. Pod koniec gry ponownie jest mniej możliwych pozycji, a więc łatwiej jest wyszukiwać. Ale tutaj to komputer ma wiedzę: komputerowa analiza końcówek wykracza daleko poza ludzkie możliwości. Początkujący ludzie mogą wygrać końcową rozgrywkę typu „król i wieża kontra król” (KRK), przestrzegając kilku prostych zasad. Inne zakończenia, takie jak król, goniec i skoczek kontra król (KBNK), są trudne do opanowania i nie mają zwięzłego opisu strategii. Z drugiej strony komputer może całkowicie rozwiązać grę końcową, tworząc politykę, która jest mapowaniem z każdego możliwego stanu do najlepszego ruchu w tym stanie. Wtedy komputer może grać perfekcyjnie, wyszukując właściwy ruch w tej tabeli. Stół jest tworzony przez wsteczne wyszukiwanie minimaksowe: zacznij od rozważenia wszystkich sposobów umieszczenia pionków KBNK na planszy. Niektóre pozycje to wygrane białych; oznacz je jako takie. Następnie odwróć zasady gry w szachy, aby wykonywać ruchy odwrotne, a nie ruchy. Każdy ruch białych, który bez względu na to, jakim ruchem odpowiedzą czarne, kończy się na pozycji oznaczonej jako wygrana, również musi być wygraną. Kontynuuj poszukiwania, aż wszystkie możliwe pozycje zostaną rozstrzygnięte jako wygrana, przegrana lub remis, a będziesz mieć nieomylną tabelę przeglądową dla wszystkich końcówek z tymi figurami. Zostało to zrobione nie tylko dla końcówek KBNK, ale dla wszystkich końcówek z siedmioma lub mniej kawałkami. Tabele zawierają 400 bilionów pozycji. Ośmioczęściowy stół wymagałby 40 biliardów pozycji.

Przycinanie alfa-beta przycina gałęzie drzewa, które nie mogą mieć wpływu na ostateczną ocenę, ale przycinanie do przodu przycina ruchy, które wydają się słabymi ruchami, ale mogą być dobrymi. W ten sposób strategia oszczędza czas obliczeń, ryzykując błąd. W terminologii Shannona jest to strategia typu B. Oczywiście większość szachistów robi to, biorąc pod uwagę tylko kilka ruchów z każdej pozycji (przynajmniej świadomie) wszystkie możliwe ruchy. Niestety takie podejście jest dość niebezpieczne, ponieważ nie gwarantujemy, że najlepszy ruch nie zostanie przycięty. PROBCUT lub algorytm cięcia probabilistycznego (Buro, 1995) to przycinająca do przodu wersja wyszukiwania alfa-beta, która wykorzystuje statystyki uzyskane z wcześniejszych doświadczeń, aby zmniejszyć prawdopodobieństwo, że najlepszy ruch zostanie przycięty. Wyszukiwanie alfa-beta usuwa każdy węzeł, który prawdopodobnie znajduje się poza (α β) bieżącym oknem. PROBCUT przycina również węzły, które prawdopodobnie znajdują się poza oknem. Oblicza to prawdopodobieństwo, wykonując płytkie wyszukiwanie w celu obliczenia wartości węzła z kopii zapasowej, a następnie wykorzystując wcześniejsze doświadczenia do oszacowania prawdopodobieństwa, że ​​wynik na głębokości w drzewie będzie poza (α, β) . Buro zastosował tę technikę w swoim programie Othello, LOGISTELLO, i odkrył, że wersja jego programu z PROBCUT pokonuje wersję regularną w 64% przypadków, nawet jeśli zwykła wersja miała dwa razy więcej czasu. Inna technika, późna redukcja ruchów, działa przy założeniu, że porządkowanie ruchów zostało wykonane dobrze, a zatem ruchy, które pojawiają się później na liście możliwych ruchów, są mniej prawdopodobne, że będą dobrymi ruchami. Ale zamiast całkowicie je przycinać, po prostu zmniejszamy głębokość, do której przeszukujemy te ruchy, oszczędzając w ten sposób czas. Jeśli zredukowane wyszukiwanie wróci z wartością wyższą od aktualnej wartości α, możemy ponownie przeprowadzić wyszukiwanie z pełną głębokością. Połączenie wszystkich opisanych tutaj technik daje w wyniku program, który może grać w wiarygodne szachy (lub inne gry). Załóżmy, że zaimplementowaliśmy funkcję oceny dla szachów, rozsądny test odcięcia z wyszukiwaniem stanu spoczynku. Załóżmy również, że po miesiącach żmudnego bitowania, na najnowszym komputerze PC możemy wygenerować i ocenić około miliona węzłów na sekundę. Współczynnik rozgałęzienia dla szachów wynosi średnio około 35, a 355 to około 50 milionów, więc gdybyśmy użyli wyszukiwania minimaksowego, moglibyśmy patrzeć w przyszłość tylko na pięć warstw w około minutę obliczeń; zasady konkurencji nie dałyby nam wystarczająco dużo czasu na przeszukanie sześciu warstw. Choć nie jest niekompetentny, taki program może zostać pokonany przez przeciętnego szachistę, który od czasu do czasu może zaplanować sześć lub osiem partii do przodu. Dzięki wyszukiwaniu alfa-beta i dużej tabeli transpozycji dochodzimy do około 14 warstw, co daje ekspercki poziom gry. Moglibyśmy zamienić nasz komputer na stację roboczą z 8 procesorami graficznymi, uzyskując ponad miliard węzłów na sekundę, ale aby uzyskać status arcymistrza, nadal potrzebowalibyśmy rozbudowanej funkcji oceny i dużej bazy danych ruchów końcowych. Najlepsze programy szachowe, takie jak STOCKFISH, mają to wszystko, często osiągając głębokość 30 lub więcej w drzewie wyszukiwania i znacznie przekraczając możliwości każdego gracza.

Następnym krokiem jest zmodyfikowanie funkcji ALPHA-BETA-SEARCH tak, aby wywoływała heurystyczną funkcję EVAL, gdy konieczne jest odcięcie wyszukiwania. Zamieniamy dwa wiersze na liście, które wspominają o IS-TERMINAL, następującym wierszem:

if game.IS-CUTOFF(stan, głębokość) return game.EVAL(stan, player), null

Musimy również zorganizować trochę księgowości, aby bieżąca głębokość była zwiększana przy każdym wywołaniu rekurencyjnym. Najprostsze podejście do kontrolowania ilości wyszukiwań

jest ustawienie stałego limitu głębokości, tak aby IS-CUTOFF(stan, głębokość) zwracał wartość true dla wszystkich głębokości większych niż pewna ustalona głębokość (jak również dla wszystkich stanów końcowych). Głębokość jest wybierana tak, aby ruch został wybrany w wyznaczonym czasie. Bardziej niezawodnym podejściem jest zastosowanie pogłębiania iteracyjnego. (Patrz rozdział 3 .) Gdy skończy się czas, program zwraca ruch wybrany przez najgłębsze zakończone wyszukiwanie. Jako bonus, jeśli w każdej rundzie iteracyjnego pogłębiania będziemy trzymać wpisy w tabeli transpozycji, kolejne rundy będą szybsze i możemy wykorzystać oceny do poprawy kolejności ruchów. Te proste podejścia mogą prowadzić do błędów ze względu na przybliżony charakter funkcji oceny. Rozważmy ponownie prostą funkcję oceny szachów opartą na przewadze materialnej. Załóżmy, że program szuka do granicy głębokości, osiągając pozycję na rysunku (b), gdzie czarne są przed skoczkiem i dwoma pionkami. Zgłosi to jako wartość heurystyczną stanu, tym samym oświadczając, że stan jest prawdopodobną wygraną Blacka. Ale następny ruch białych zbija hetmana czarnych bez żadnej rekompensaty. Stąd pozycja jest faktycznie korzystna dla białych, ale można to zobaczyć tylko patrząc w przyszłość. Funkcja oceny powinna być stosowana tylko do pozycji, które są spokojne, to znaczy do pozycji, w których nie ma żadnego oczekującego ruchu (takiego jak zbicie hetmana), który mógłby szalenie zmienić ocenę. Dla pozycji nie spoczynkowych IS-CUTOFF zwraca wartość fałsz, a wyszukiwanie jest kontynuowane aż do osiągnięcia pozycji spoczynkowych. To dodatkowe poszukiwanie spokoju jest czasami ograniczone do rozważenia tylko niektórych rodzajów ruchów, takich jak ruchy przechwytywania, które szybko rozwiążą niepewność pozycji. Efekt horyzontu jest trudniejszy do wyeliminowania. Pojawia się, gdy program ma do czynienia z ruchem przeciwnika, który powoduje poważne szkody i jest ostatecznie nieunikniony, ale można go tymczasowo uniknąć, stosując taktyki opóźniające. Rozważ pozycję w szachach na rysunku. Jasne jest, że czarny goniec nie ma możliwości ucieczki. Na przykład biała wieża może ją zbić, przesuwając się na h1, potem a1, potem a2; przechwytywanie na głębokości 6 warstw.

Ale czarne mają sekwencję ruchów, które przesuwają zbicie gońca „za horyzont”. Załóżmy, że Black wyszukuje do 8 warstw. Większość ruchów czarnych doprowadzi do ostatecznego zbicia gońca i tym samym zostanie oznaczona jako „złe” ruchy. Ale czarne rozważą również sekwencję ruchów, która zaczyna się od szachowania króla pionkiem i skłaniania króla do zbicia piona. Czarne mogą wtedy zrobić to samo z drugim pionkiem. Zajmuje to wystarczająco dużo ruchów, aby zbicie gońca nie zostało odkryte podczas pozostałej części poszukiwań czarnych. Czarny myśli, że linia gry uratowała gońca za cenę dwóch pionków, podczas gdy w rzeczywistości wszystko, co zrobił, to zmarnowanie pionów i przesunięcie nieuchronnego bicia gońca poza horyzont, który czarne mogą zobaczyć. Jedną ze strategii łagodzenia efektu horyzontu jest umożliwienie pojedynczych wydłużeń, ruchów, które są „wyraźnie lepsze” niż wszystkie inne ruchy w danej pozycji, nawet jeśli wyszukiwanie zostałoby normalnie przerwane w tym momencie. W naszym przykładzie przeszukanie wykazało, że trzy ruchy białej wieży z h2 na h1, potem z h1 na a1, a następnie zbicie gońca na a2 przez a1 są z kolei wyraźnie lepszymi ruchami, więc nawet jeśli sekwencja pionków ruchy wypychają nas na horyzont, te wyraźnie lepsze ruchy będą miały szansę na rozszerzenie poszukiwań. To sprawia, że ​​drzewo jest głębsze, ale ponieważ zwykle jest niewiele pojedynczych rozszerzeń, strategia nie dodaje wielu węzłów do drzewa i okazała się skuteczna w praktyce.

Heurystyczna funkcja oceny Eval (s,p) zwraca graczowi p oszacowanie oczekiwanej użyteczności stanu s, podobnie jak funkcje heurystyczne z rozdziału 3 zwracają oszacowanie odległości do celu. Dla stanów końcowych musi być tak, że Eval(s,p) = Utility(s,p), a dla stanów nieterminalnych ocena musi być gdzieś pomiędzy stratą a wygraną:

Utility(loss,p) ≤    Eval(s,p)  ≤ Utility(winn,p)

Co poza tymi wymaganiami zapewnia dobrą funkcję oceny? Po pierwsze, obliczenia nie mogą trwać zbyt długo! (Chodzi o szybsze wyszukiwanie). Po drugie, funkcja oceny powinna być silnie skorelowana z rzeczywistymi szansami na wygraną. Można się zastanawiać nad wyrażeniem „szanse na wygraną”. W końcu szachy nie są grą losową: znamy obecny stan z całą pewnością i nie ma w tym żadnych kości; jeśli żaden z graczy nie popełni błędu, wynik jest z góry określony. Ale jeśli wyszukiwanie musi zostać odcięte w stanach nieterminalnych, wówczas algorytm będzie z konieczności niepewny co do końcowych wyników tych stanów (nawet jeśli tę niepewność można rozwiązać przy nieskończonych zasobach obliczeniowych).

Ukonkretnijmy ten pomysł. Większość funkcji oceny działa poprzez obliczanie różnych cech stanu — na przykład w szachach mielibyśmy cechy liczby białych pionków, czarnych pionków, białych hetmanów, czarnych hetmanów i tak dalej. Cechy wzięte razem definiują różne kategorie lub klasy równoważności stanów: stany w każdej kategorii mają te same wartości dla wszystkich cech. Na przykład jedna kategoria może zawierać wszystkie gry końcowe z dwoma pionkami i jednym pionkiem. Każda dana kategoria będzie zawierać pewne stany, które prowadzą (przy doskonałej grze) do wygranych, niektóre prowadzą do remisów, a niektóre prowadzą do przegranych.

Funkcja oceny nie wie, które stany są jakimi, ale może zwrócić pojedynczą wartość, która szacuje proporcję stanów z każdym wynikiem. Załóżmy na przykład, że nasze doświadczenie sugeruje, że 82% stanów napotkanych w kategorii dwóch pionków kontra jeden pion prowadzi do zwycięstwa (użyteczność +1); 2% do straty (0) i 16% do remisu (1/2) . Wówczas rozsądną oceną dla stanów w kategorii jest wartość oczekiwana:

(0,82 x +1) + (0,02 x + 0) + (0,16 x 1/2) = 0,90

W zasadzie wartość oczekiwaną można określić dla każdej kategorii stanów, co skutkuje funkcją oceny, która działa dla dowolnego stanu.

W praktyce tego rodzaju analiza wymaga zbyt wielu kategorii, a co za tym idzie zbyt dużego doświadczenia, aby oszacować wszystkie prawdopodobieństwa. Zamiast tego większość funkcji oceny oblicza oddzielne wkłady liczbowe z każdej cechy, a następnie łączy je, aby znaleźć łączną wartość. Od wieków szachiści opracowują sposoby oceniania wartości pozycji, używając właśnie tego pomysłu. Na przykład wprowadzające księgi szachowe podają przybliżoną wartość materialną każdej figury: każdy pionek jest wart 1, rycerz lub goniec wart jest 3, wieża 5, a hetman 9. Inne cechy, takie jak „dobra struktura pionków” i „król bezpieczeństwo” może być warte pół pionka, powiedzmy. Te wartości cech są następnie po prostu sumowane, aby uzyskać ocenę pozycji. Matematycznie ten rodzaj funkcji oceny nazywa się ważoną funkcją liniową, ponieważ można ją wyrazić jako

gdzie każde f_i jest cechą pozycji (np. „liczba białych gońców”), a każde w_i jest wagą (mówiącą, jak ważna jest ta cecha). Wagi należy znormalizować tak, aby suma zawsze mieściła się w przedziale od przegranej (0) do wygranej (+1). Pewna przewaga równoważna pionkowi daje duże prawdopodobieństwo wygranej, a bezpieczna przewaga równoważna trzem pionkom powinna dać prawie pewne zwycięstwo, jak pokazano na rysunku (a).

Powiedzieliśmy, że funkcja oceny powinna być silnie skorelowana z rzeczywistymi szansami na wygraną, ale nie musi być skorelowana liniowo: jeśli stan ma dwa razy większe prawdopodobieństwo wygrania niż stan s’, nie wymagamy, aby EVAL(S) była dwukrotnie EVAL (S’); wszystko czego potrzebujemy to, że EVAL(s) > EVAL(s)

Zsumowanie wartości cech wydaje się rozsądne, ale w rzeczywistości wiąże się z mocnym założeniem: wkład każdej cechy jest niezależny od wartości innych cech. Z tego powodu obecne programy do szachów i innych gier również wykorzystują nieliniowe kombinacje cech. Na przykład, para gońców może być warta ponad dwukrotnie więcej niż pojedynczy goniec, a goniec jest wart więcej w końcowej fazie gry niż wcześniej – gdy cecha liczby ruchów jest wysoka lub liczba pozostałych bierek jest niska. Skąd pochodzą cechy i wagi? Nie są częścią zasad szachów, ale są częścią kultury ludzkiego doświadczenia szachowego. W grach, w których tego rodzaju doświadczenie nie jest dostępne, wagi funkcji oceny można oszacować za pomocą technik uczenia maszynowego z rozdziału 22 . Zastosowanie tych technik do szachów potwierdziło, że biskup rzeczywiście jest wart około trzech pionków i wydaje się, że stulecia ludzkiego doświadczenia można odtworzyć w ciągu zaledwie kilku godzin uczenia maszynowego.

Aby wykorzystać nasz ograniczony czas obliczeń, możemy wcześnie odciąć wyszukiwanie i zastosować do stanów funkcję oceny heurystycznej, skutecznie traktując węzły nieterminalne tak, jakby były terminalami. Innymi słowy, zastępujemy funkcję UTILITY funkcją EVAL, która szacuje użyteczność stanu. Zamieniamy również test terminala na test odcięcia, który musi zwracać wartość true dla stanów końcowych, ale poza tym może swobodnie decydować, kiedy odciąć wyszukiwanie, na podstawie głębokości wyszukiwania i dowolnej właściwości stanu, który zdecyduje się wziąć pod uwagę. To daje nam wzór H-MINIMAX( s, d) na heurystyczną wartość minimax stanu na głębokości wyszukiwania d:

Skuteczność przycinania alfa-beta w dużym stopniu zależy od kolejności, w jakiej badane są stany. Na przykład na rysunku (e) i (f) nie mogliśmy w ogóle przyciąć żadnych następców D, ponieważ najgorsze następniki (z punktu widzenia MIN) zostały wygenerowane jako pierwsze.

Gdyby trzeci następca D został wygenerowany jako pierwszy, z wartością 2, bylibyśmy w stanie przyciąć dwóch pozostałych następców. Sugeruje to, że warto spróbować najpierw zbadać następców, którzy prawdopodobnie będą najlepsi. Gdyby można było to zrobić perfekcyjnie, alfa-beta musiałaby zbadać tylko O(b^m/2) węzły, aby wybrać najlepszy ruch, zamiast O(b^m) dla minimaksu. Oznacza to, że efektywnym współczynnikiem rozgałęzienia staje się pierwiastek b zamiast b – dla szachów około 6 zamiast 35. Innymi słowy, alfa-beta z doskonałą kolejnością ruchów może rozwiązać drzewo mniej więcej dwa razy głębsze niż minimax w tym samym czasie . Przy losowej kolejności ruchów całkowita liczba zbadanych węzłów będzie w przybliżeniu wynosić O(b^3m/4) dla umiarkowanego b . Teraz oczywiście nie możemy osiągnąć idealnego uporządkowania ruchów – w takim przypadku funkcja zamawiania mogłaby zostać wykorzystana do rozegrania doskonałej gry! Ale często możemy podejść dość blisko. W przypadku szachów dość prosta funkcja porządkowania (taka jak próba najpierw przechwytów, potem zagrożeń, potem ruchów do przodu, a następnie ruchów do tyłu) pozwala uzyskać mniej więcej czynnik 2 od wyniku w najlepszym przypadku O(b^m/2).

Dodanie dynamicznych schematów kolejności ruchów, takich jak wypróbowywanie najpierw ruchów, które w przeszłości uznano za najlepsze, zbliża nas do teoretycznego limitu. Przeszłość może być poprzednim posunięciem – często pozostają te same zagrożenia – lub może pochodzić z wcześniejszej eksploracji obecnego posunięcia poprzez proces iteracyjnego pogłębiania. Najpierw przeszukaj jedną warstwę głęboko i zapisz ranking ruchów na podstawie ich ocen. Następnie przeszukaj jedną warstwę głębiej, używając poprzedniego rankingu do informowania o kolejności ruchów; i tak dalej. Wydłużony czas wyszukiwania wynikający z iteracyjnego pogłębiania może być więcej niż nadrobiony dzięki lepszemu porządkowaniu ruchów. Najlepsze ruchy są znane jako zabójcze ruchy, a wypróbowanie ich w pierwszej kolejności nazywa się heurystyką zabójczych ruchów.

Zauważyliśmy, że nadmiarowe ścieżki do powtarzających się stanów mogą powodować wykładniczy wzrost kosztów wyszukiwania, a prowadzenie tabeli stanów, które zostały wcześniej osiągnięte, może rozwiązać ten problem. W przeszukiwaniu drzewa gry mogą wystąpić powtarzające się stany z powodu transpozycji — różnych permutacji sekwencji ruchu, które kończą się w tej samej pozycji, a problem można rozwiązać za pomocą tabeli transpozycji, która buforuje wartości heurystyczne stanów. Załóżmy na przykład, że biały ma ruch w1, na który czarny może odpowiedzieć b1 i niepowiązany ruch w2 po drugiej stronie szachownicy, na który może odpowiedzieć b2 , i że przeszukujemy sekwencję ruchów [w1,b1,w2 ,b2 ] ; nazwijmy wynikowy stan . Po zbadaniu dużego poddrzewa poniżej znajdujemy jego kopię zapasową, którą przechowujemy w tabeli transpozycji. Kiedy później przeszukujemy sekwencję ruchów , znajdujemy się ponownie i możemy wyszukać wartość zamiast powtarzać wyszukiwanie. W szachach bardzo efektywne jest wykorzystanie tabel transpozycji, co pozwala nam podwoić osiągalną głębokość wyszukiwania w tym samym czasie. Nawet przy przycinaniu alfa-beta i sprytnym porządkowaniu ruchów minimax nie zadziała w grach takich jak szachy i Go, ponieważ wciąż jest zbyt wiele stanów do zbadania w dostępnym czasie. W pierwszym artykule na temat gier komputerowych, Programowanie komputera do gry w szachy, Claude Shannon rozpoznał ten problem i zaproponował dwie strategie: strategia typu A uwzględnia wszystkie możliwe ruchy do określonej głębokości w drzewie wyszukiwania, a następnie wykorzystuje heurystykę funkcja oceny do oszacowania użyteczności stanów na tej głębokości. Bada szeroką, ale płytką część drzewa. Strategia typu B ignoruje ruchy, które wyglądają źle i podąża za obiecującymi liniami „tak daleko, jak to możliwe”. Bada głęboką, ale wąską część drzewa. Historycznie, większość programów szachowych należała do Typu A (który omówimy w następnej sekcji), podczas gdy programy Go są częściej Typu B (omówione w Sekcji 5.4), ponieważ współczynnik rozgałęzienia jest znacznie wyższy w Go. Niedawno programy typu B pokazały grę na poziomie mistrzów świata w różnych grach, w tym w szachy

Liczba stanów gry jest wykładnicza na głębokości drzewa. Żaden algorytm nie jest w stanie całkowicie wyeliminować wykładnika, ale czasami możemy przeciąć go o połowę, obliczając prawidłową decyzję minimaksową bez badania każdego stanu poprzez przycinanie dużych części drzewa, które nie mają wpływu na wynik. Konkretna technika, którą badamy, nazywa się przycinaniem alfa-beta. Rozważmy ponownie dwuwarstwowe drzewo gry . Przejdźmy jeszcze raz przez obliczenie optymalnej decyzji, tym razem zwracając szczególną uwagę na to, co wiemy na każdym etapie procesu. Kroki są wyjaśnione na rysunku. Wynikiem jest to, że możemy zidentyfikować decyzję minimax bez oceny dwóch węzłów liści.

Innym sposobem spojrzenia na to jest uproszczenie formuły MINIMAX. Niech dwa nieocenione następniki węzła C na rysunku mają wartości x i y . Wtedy wartość węzła głównego jest dana przez

Innymi słowy, wartość pierwiastka, a tym samym decyzja o minimaksie, są niezależne od wartości liści x i y i dlatego można je przycinać. Przycinanie alfa-beta może być stosowane do drzew o dowolnej głębokości i często można przycinać całe poddrzewa, a nie tylko liście. Ogólna zasada jest następująca: rozważ węzeł n gdzieś w drzewie, taki, że Gracz ma wybór przejścia do . Jeśli Gracz ma lepszy wybór albo na tym samym poziomie (np. m’ na rysunku 5.6 ) lub w dowolnym punkcie wyżej w drzewie (np. m na rysunku), to nigdy nie przejdzie do . Więc kiedy już wystarczająco dowiedzieliśmy się o n (poprzez zbadanie niektórych jego potomków), aby dojść do tego wniosku, możemy je przyciąć.

Pamiętaj, że wyszukiwanie minimaksowe jest na pierwszym miejscu, więc w dowolnym momencie musimy brać pod uwagę węzły wzdłuż pojedynczej ścieżki w drzewie. Przycinanie alfa-beta bierze swoją nazwę od dwóch dodatkowych parametrów w MAX-VALUE (stan α , β) , które opisują granice wartości kopii zapasowej, które pojawiają się w dowolnym miejscu na ścieżce:

α = wartość najlepszego (tj. najwyższej wartości) wyboru, jaki do tej pory znaleźliśmy w dowolnym punkcie wyboru na ścieżce dla MAX. Pomyśl: α = „przynajmniej”.

β = wartość najlepszego (tj. najniższej wartości) wyboru, jaki do tej pory znaleźliśmy w dowolnym punkcie wyboru na ścieżce dla MIN. Pomyśl: β = „co najwyżej”.

Wyszukiwanie alfa-beta aktualizuje wartości α i β w miarę postępu i usuwa pozostałe gałęzie w węźle (tj. kończy wywołanie rekurencyjne), gdy tylko wiadomo, że wartość bieżącego węzła jest gorsza niż bieżąca alfa lub wartość beta odpowiednio dla MAX lub MIN.