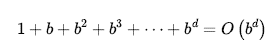Miesiąc: sierpień 2021

Najpopularniejszym algorytmem świadomego wyszukiwania jest wyszukiwanie A* (wymawiane „wyszukiwanie z gwiazdką A”), wyszukiwanie „najlepsze-pierwsze”, które wykorzystuje funkcję oceny

f(n) = h(n)+ g(n)

gdzie g(n) to koszt ścieżki od stanu początkowego do węzła n, a h(n) to szacowany koszt najkrótszej ścieżki z n do stanu docelowego, więc mamy

f(n) = szacowany koszt najlepszej ścieżki, która biegnie od n do celu.

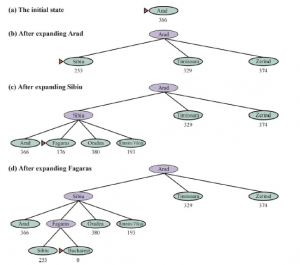
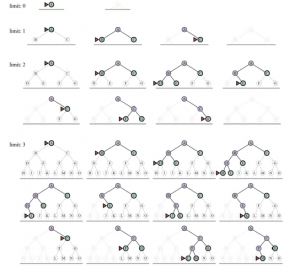
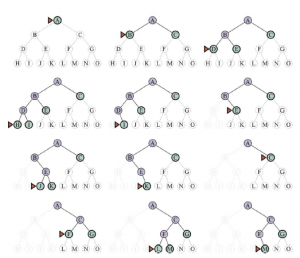
Na rysunku pokazujemy postęp wyszukiwania A*, którego celem jest dotarcie do Bukaresztu.

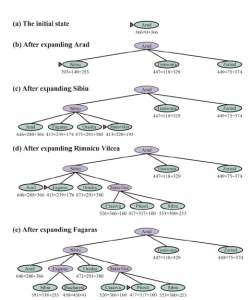
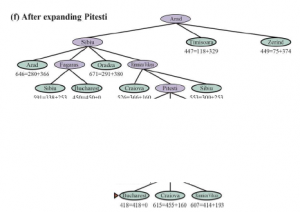
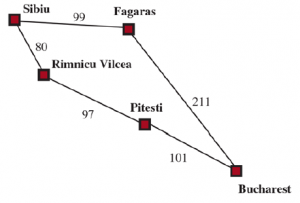
Wartości g obliczono z kosztów działań na Rysunku 3.1 , a wartości hSLD podano na Rysunku 3.16 . Zauważ, że Bukareszt po raz pierwszy pojawia się na granicy w kroku (e), ale nie jest wybrany do ekspansji (a zatem nie jest wykrywany jako rozwiązanie), ponieważ przy f = 450 nie jest to najtańszy węzeł na granicy — byłoby to Pitesti, przy f= A17. Innym sposobem na powiedzenie tego jest to, że może istnieć rozwiązanie przez Pitesti, którego koszt jest tak niski, jak 417, więc algorytm nie zadowoli się rozwiązaniem, które kosztuje 450. W kroku (f) inna droga do Bukaresztu jest teraz najniższa -koszt węzła, przy f = 418, więc jest wybierany i wykrywany jako rozwiązanie optymalne.

Wyszukiwanie* zakończone. To, czy A* jest optymalne pod względem kosztów, zależy od pewnych właściwości heurystyki. Kluczową właściwością jest dopuszczalność: dopuszczalna heurystyka to taka, która nigdy nie przecenia kosztów osiągnięcia celu. (Dopuszczalna heurystyka jest zatem optymistyczna.) Przy dopuszczalnej heurystyce A* jest optymalny pod względem kosztów, co możemy wykazać za pomocą dowodu przez sprzeczność. Załóżmy, że optymalna ścieżka ma koszt C*, ale algorytm zwraca ścieżkę o koszcie C > C*. Następnie musi istnieć jakiś węzeł n, który znajduje się na optymalnej ścieżce i jest nierozwinięty (ponieważ gdyby wszystkie węzły na optymalnej ścieżce zostały rozwinięte, to zwrócilibyśmy to optymalne rozwiązanie). Zatem używając notacji g*(n) do oznaczenia kosztu ścieżki optymalnej od początku do n i h*(n) do oznaczenia kosztu ścieżki optymalnej od n do najbliższego celu, mamy:

f (n) > C^∗ (w przeciwnym razie n zostałoby rozszerzone)

f (n) = g (n) + h (n) (z definicji)

f (n) = g^∗ (n) + h (n) (ponieważ n jest na optymalnej ścieżce)

f (n) ≤ g^∗ (n) + h^∗ (n) (ze względu na dopuszczalność, h (n) ≤ h^∗ (n))

f (n) ≤ C^∗ (z definicji, C^∗ = g^∗ (n) + h^∗ (n))

Pierwsza i ostatnia linia tworzą sprzeczność, więc założenie, że algorytm może zwrócić ścieżkę suboptymalną, musi być błędne – musi być tak, że A* zwraca tylko ścieżki optymalne kosztowo. Nieco silniejsza właściwość nazywa się konsystencją. Heurystyka h(n) jest niesprzeczna, jeśli dla każdego węzła n i każdego następnika n’ z n wygenerowanego przez akcję a mamy:

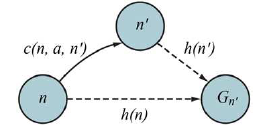
h(n) ≤ c(n, a, n′) + h(n′).

Jest to forma nierówności trójkąta, która stanowi, że bok trójkąta nie może być dłuższy niż suma pozostałych dwóch boków. Przykładem spójnej heurystyki jest odległość w linii prostej h_SLD, którą wykorzystaliśmy, aby dostać się do Bukaresztu.

Każda spójna heurystyka jest dopuszczalna (ale nie odwrotnie), więc przy spójnej heurystyce A* jest optymalny pod względem kosztów. Ponadto, dzięki spójnej heurystyce, za pierwszym razem, gdy osiągniemy stan, będzie on na optymalnej ścieżce, więc nigdy nie będziemy musieli ponownie dodawać stanu do granicy i nigdy nie musimy zmieniać wpisu w osiągniętym. Ale przy niespójnej heurystyce możemy skończyć z wieloma ścieżkami osiągającymi ten sam stan, a jeśli każda nowa ścieżka ma niższy koszt ścieżki niż poprzednia, wtedy skończymy z wieloma węzłami dla tego stanu na granicy, co będzie nas kosztować zarówno czas, jak i przestrzeń. Z tego powodu niektóre implementacje A* dbają o to, aby tylko raz wprowadzić stan do granicy, a jeśli zostanie znaleziona lepsza ścieżka do stanu, wszystkie następniki stanu są aktualizowane (co wymaga, aby węzły miały również wskaźniki podrzędne jako wskaźniki nadrzędne). Te komplikacje doprowadziły wielu realizatorów do uniknięcia niespójnych heurystyk, ale Felner przekonuje, że w praktyce najgorsze efekty zdarzają się rzadko i nie należy obawiać się niekonsekwentnych heurystyk.

Przy niedopuszczalnej heurystyce A* może być lub nie być optymalny pod względem kosztów. Oto dwa przypadki, w których tak jest: Po pierwsze, jeśli istnieje chociaż jedna ścieżka optymalna pod względem kosztów, na której h(n) jest dopuszczalne dla wszystkich n węzłów na ścieżce, wtedy ta ścieżka zostanie znaleziona, bez względu na to, co mówi heurystyka

stwierdza poza ścieżką. Po drugie, jeśli optymalne rozwiązanie ma koszt C*, a drugie najlepsze ma koszt C2 i h(n), jeśli przeszacowuje niektóre koszty, ale nigdy o więcej niż C2 – C*, to A* gwarantuje zwrócenie rozwiązań optymalnych kosztowo.

Chciwe przeszukiwanie „najlepsze-pierwsze” jest formą przeszukiwania „najlepsze-pierwsze”, które rozwija najpierw węzeł z najniższą wartością – węzeł, który wydaje się być najbliżej celu – na tej podstawie, że może to szybko doprowadzić do rozwiązania. Zatem funkcja oceny f(n) = g(n).

Zobaczmy, jak to działa w przypadku problemów ze znajdowaniem tras w Rumunii; używamy heurystyki odległości w linii prostej, którą nazwiemy h_SLD. Jeśli celem jest Bukareszt, musimy znać odległości do Bukaresztu w linii prostej, które pokazano tu .

Na przykład h_SLD(Arad) = 366. Zauważ, że wartości h_SLD nie można obliczyć na podstawie problemu

sam opis (czyli funkcje AKCJE i WYNIK). Co więcej, potrzeba pewnej wiedzy o świecie, aby wiedzieć, że h_SLD jest skorelowane z rzeczywistymi odległościami drogowymi i dlatego jest użyteczną heurystyką.

Rysunek przedstawia postęp zachłannego wyszukiwania „najpierw najlepszy” przy użyciu h_SLD w celu znalezienia drogi z Aradu do Bukaresztu.

Pierwszym węzłem, który zostanie rozszerzony z Arad, będzie Sibiu, ponieważ heurystyka mówi, że jest bliżej Bukaresztu niż Zerind czy Timisoara. Następnym rozwiniętym węzłem będzie Fagaras, ponieważ jest teraz najbliżej według heurystyki. Fagaras z kolei generuje Bukareszt, który jest celem. W przypadku tego konkretnego problemu zachłanne wyszukiwanie „najpierw najlepszy” przy użyciu hSLD znajduje rozwiązanie bez rozszerzania węzła, który nie znajduje się na ścieżce rozwiązania. Znalezione rozwiązanie nie ma jednak optymalnych kosztów: trasa przez Sibiu i Fagaras do Bukaresztu jest o 32 mile dłuższa niż trasa przez Rimnicu Vilcea i Pitesti. Dlatego algorytm jest nazywany „chciwym” – w każdej iteracji stara się zbliżyć do celu jak tylko może, ale zachłanność może prowadzić do gorszych wyników niż bycie ostrożnym. Chciwe przeszukiwanie grafu „najlepszy-pierwszy” jest kompletne w skończonych przestrzeniach stanów, ale nie w nieskończonych. Najgorszy przypadek złożoności czasowej i przestrzennej to O(|V|). Jednak przy dobrej funkcji heurystycznej złożoność można znacznie zmniejszyć, przy pewnych problemach osiągających O(bm).

W tej sekcji pokazano, w jaki sposób świadoma strategia wyszukiwania – korzystająca ze wskazówek specyficznych dla domeny dotyczących lokalizacji celów – może skuteczniej znajdować rozwiązania niż strategia oparta na niedoinformowaniu. Wskazówki mają postać funkcji heurystycznej, oznaczonej jako h(n).

h(n) = szacowany koszt najtańszej ścieżki od stanu w węźle n do stanu docelowego.

Na przykład w problemach ze znajdowaniem trasy możemy oszacować odległość od aktualnego stanu do celu, obliczając odległość w linii prostej na mapie między dwoma punktami.

To porównanie dotyczy wersji wyszukiwania podobnych do drzewa, które nie sprawdzają powtarzających się stanów. W przypadku przeszukiwań grafów, które sprawdzają, główne różnice polegają na tym, że wyszukiwanie w głąb jest kompletne dla skończonych przestrzeni stanów, a złożoność przestrzenna i czasowa jest ograniczona rozmiarem przestrzeni stanów (liczba wierzchołków i krawędzi, |V| + |E|). Ocena algorytmów wyszukiwania. jest czynnikiem rozgałęzienia; m to maksymalna głębokość drzewa wyszukiwania; d jest głębokością najpłytszego rozwiązania lub gdy m nie ma rozwiązania; l to limit głębokości. Zastrzeżenia indeksu górnego są następujące: zupełna, jeśli b jest skończona, a przestrzeń stanów ma rozwiązanie lub jest skończona. kompletna, jeśli wszystkie koszty działania są optymalne pod względem kosztów ≥ ε  0, jeśli wszystkie koszty działania są identyczne; jeśli obydwa kierunki są oparte na szerokościach lub jednolitych kosztach.

Algorytmy, które omówiliśmy do tej pory, zaczynają się od stanu początkowego i mogą osiągnąć dowolny z wielu możliwych stanów docelowych. Alternatywne podejście zwane przeszukiwaniem dwukierunkowym jednocześnie przeszukuje w przód od stanu początkowego i wstecz od stanu(ów) docelowego(ych), mając nadzieję, że oba wyszukiwania się spotkają. Motywacja jest taka, że b^d/2 +  b^d/2 to znacznie mniej niż b^d (np. 50 000 razy mniej, gdy b = d = 10).

Aby to zadziałało, musimy śledzić dwie granice i dwie tabele osiągniętych stanów, a także musimy być w stanie rozumować wstecz: jeśli stan s’ jest następcą w kierunku do przodu, to musimy wiedzieć, że jest następca s’ w kierunku wstecznym. Mamy rozwiązanie, gdy zderzają się dwie granice.

Istnieje wiele różnych wersji wyszukiwania dwukierunkowego, podobnie jak istnieje wiele różnych algorytmów wyszukiwania jednokierunkowego. W tej sekcji opisujemy dwukierunkowe wyszukiwanie od najlepszej do pierwszej. Chociaż istnieją dwie oddzielne granice, węzeł, który ma zostać rozwinięty jako następny, jest zawsze takim, który ma minimalną wartość funkcji oceny, po obu stronach granicy. Gdy funkcją oceny jest koszt ścieżki, otrzymujemy dwukierunkowe przeszukiwanie o jednolitym koszcie, a jeśli kosztem optymalnej ścieżki jest C^*, to żaden węzeł z kosztem > C^*/2 nie zostanie rozszerzony. Może to spowodować znaczne przyspieszenie. Ogólny algorytm dwukierunkowego wyszukiwania „najlepszy-pierwszy” pokazano na rysunku 3.14. Przekazujemy dwie wersje zadania i funkcji oceny, jedną w kierunku do przodu (subscript ) i jedną w kierunku wstecznym (subscript ). Gdy funkcją oceny jest koszt ścieżki, wiemy, że pierwsze znalezione rozwiązanie będzie rozwiązaniem optymalnym, ale z różnymi funkcjami oceny, co niekoniecznie jest prawdą. Dlatego śledzimy najlepsze znalezione do tej pory rozwiązanie i być może będziemy musieli aktualizować je kilka razy, zanim test ZAKOŃCZONY wykaże, że nie ma lepszego rozwiązania.

Dwukierunkowe wyszukiwanie „najlepszy-pierwszy” zachowuje dwie granice i dwie tabele osiągniętych stanów. Gdy ścieżka w jednej granicy osiąga stan, który został osiągnięty również w drugiej połowie poszukiwań, obie ścieżki są łączone (funkcją JOIN-NODES) w celu utworzenia rozwiązania. Pierwsze rozwiązanie, które otrzymamy, nie gwarantuje, że będzie najlepsze; funkcja ZAKOŃCZONA określa, kiedy przestać szukać nowych rozwiązań.

Aby uchronić wyszukiwanie w głąb przed wędrowaniem po nieskończonej ścieżce, możemy użyć wyszukiwania z ograniczeniem w głąb, wersji wyszukiwania w głąb, w której podajemy limit głębokości l i traktujemy wszystkie węzły na głębokości tak, jakby nie miały następców (zobacz Rysunek 3.12. Złożoność czasowa to O(b^l), a złożoność przestrzeni to O(bl). Niestety, jeśli dokonamy złego wyboru, algorytm nie zdoła znaleźć rozwiązania, czyniąc je ponownie niekompletnym.Aby uchronić wyszukiwanie w głąb przed wędrowaniem po nieskończonej ścieżce, możemy użyć wyszukiwania z ograniczeniem w głąb, wersji wyszukiwania w głąb, w której podajemy limit głębokości l i traktujemy wszystkie węzły na głębokości tak, jakby nie miały następców (Złożoność czasowa to O(b^l), a złożoność przestrzeni to O(bl). Niestety, jeśli dokonamy złego wyboru, algorytm nie zdoła znaleźć rozwiązania, czyniąc je ponownie niekompletnym.

Pogłębianie iteracyjne i wyszukiwanie podobne do drzewa z ograniczeniem głębokości. Pogłębianie iteracyjne wielokrotnie stosuje wyszukiwanie o ograniczonej głębokości z rosnącymi limitami. Zwraca jeden z trzech różnych typów wartości: albo węzeł rozwiązania; lub awaria, gdy wyczerpała wszystkie węzły i udowodniła, że nie ma rozwiązania na żadnej głębokości; lub odcięcie, co oznacza, że rozwiązanie może znajdować się na głębokości większej niż l. Jest to algorytm wyszukiwania podobny do drzewa, który nie śledzi osiągniętych stanów, a zatem zużywa znacznie mniej pamięci niż wyszukiwanie „najlepsze pierwsze”, ale wiąże się z ryzykiem wielokrotnego odwiedzania tego samego stanu na różnych ścieżkach. Ponadto, jeśli kontrola IS-CYCLE nie sprawdza wszystkich cykli, algorytm może zostać złapany w pętlę. Ponieważ przeszukiwanie w głąb jest przeszukiwaniem podobnym do drzewa, nie możemy generalnie powstrzymać go przed marnowaniem czasu na nadmiarowe ścieżki, ale możemy wyeliminować cykle kosztem czasu obliczeniowego. Jeśli spojrzymy tylko na kilka ogniw w łańcuchu nadrzędnym, możemy złapać większość cykli; dłuższe cykle są obsługiwane przez ograniczenie głębokości. Czasami na podstawie znajomości problemu można wybrać dobry limit głębokości. Na przykład na mapie Rumunii znajduje się 20 miast. Dlatego l = 19 , jest poprawną granicą. Ale gdybyśmy dokładnie przestudiowali mapę, odkrylibyśmy, że do każdego miasta można dotrzeć z dowolnego innego miasta w maksymalnie 9 akcjach. Ta liczba, znana jako średnica grafu w przestrzeni stanów, daje nam lepszy limit głębokości, co prowadzi do bardziej wydajnego wyszukiwania z ograniczeniem głębokości. Jednak w przypadku większości problemów nie będziemy znać dobrego limitu głębokości, dopóki nie rozwiążemy problemu. Iteracyjne wyszukiwanie pogłębiające rozwiązuje problem wyboru dobrej wartości przez wypróbowanie wszystkich wartości: najpierw 0, potem 1, potem 2 itd., dopóki nie zostanie znalezione rozwiązanie lub wyszukiwanie z ograniczeniem wgłębnym zwraca wartość niepowodzenia, a nie wartość odcięcia . Algorytm pokazano na rysunku powyżej. Pogłębianie iteracyjne łączy wiele zalet wyszukiwania w głąb i wszerz. Podobnie jak wyszukiwanie w głąb, jego wymagania dotyczące pamięci są skromne: O(bd), gdy istnieje rozwiązanie, lub O(bm) w skończonych przestrzeniach stanów bez rozwiązania. Podobnie jak przeszukiwanie wszerz, pogłębianie iteracyjne jest optymalne dla problemów, w których wszystkie działania mają ten sam koszt i są kompletne w skończonych acyklicznych przestrzeniach stanów lub w dowolnej skończonej przestrzeni stanów, gdy sprawdzamy węzły pod kątem cykli na całej ścieżce. Złożoność czasowa wynosi O(b^d), gdy istnieje rozwiązanie, lub O(b^m), gdy nie ma. Każda iteracja iteracyjnego wyszukiwania pogłębiającego generuje nowy poziom, w taki sam sposób jak wyszukiwanie wszerz, ale wszerz robi to poprzez przechowywanie wszystkich węzłów w pamięci, podczas gdy pogłębianie iteracyjne robi to poprzez powtarzanie poprzednich poziomów, oszczędzając w ten sposób pamięć kosztem więcej czasu. Rysunek przedstawia cztery iteracje pogłębiania iteracyjnego wyszukiwania na drzewie wyszukiwania binarnego, gdzie rozwiązanie znajduje się w czwartej iteracji.

Cztery iteracje iteracyjnego pogłębiania poszukiwania celu M na drzewie binarnym, z limitem głębokości wahającym się od 0 do 3. Zauważ, że węzły wewnętrzne tworzą jedną ścieżkę. Trójkąt oznacza węzeł do rozwinięcia w następnej kolejności; zielone węzły z ciemnymi konturami znajdują się na granicy; bardzo słabe węzły prawdopodobnie nie mogą być częścią rozwiązania z tym ograniczeniem głębokości. Pogłębiające wyszukiwanie iteracyjne może wydawać się marnotrawstwem, ponieważ stany w górnej części drzewa wyszukiwania są wielokrotnie generowane ponownie. Ale dla wielu przestrzeni stanów większość węzłów znajduje się na dolnym poziomie, więc nie ma większego znaczenia, że górne poziomy się powtarzają. W iteracyjnym wyszukiwaniu pogłębiającym węzły na najniższym poziomie (głębokość ) są generowane raz, te na kolejnym poziomie są generowane dwukrotnie i tak dalej, aż do dzieci korzenia, które są generowane razy. Zatem całkowita liczba węzłów wygenerowanych w najgorszym przypadku wynosi

co daje złożoność czasową O(b^d) – asymptotycznie taką samą jak przeszukiwanie wszerz. Na przykład, jeśli b = 10 i d = 5, liczby to

Jeśli naprawdę martwisz się powtarzaniem, możesz użyć podejścia hybrydowego, które uruchamia przeszukiwanie wszerz aż do zużycia prawie całej dostępnej pamięci, a następnie uruchamia iteracyjne pogłębianie ze wszystkich węzłów na granicy. Ogólnie rzecz biorąc, pogłębianie iteracyjne jest preferowaną metodą wyszukiwania bez informacji, gdy przestrzeń stanów wyszukiwania jest większa niż mieści się w pamięci, a głębokość rozwiązania nie jest znana.

Przeszukiwanie w głąb zawsze najpierw rozszerza najgłębszy węzeł na granicy. Może być wdrożony jako wezwanie do NAJLEPSZEJ PIERWSZEJ WYSZUKIWANIA, gdy funkcja oceny jest negatywna w stosunku do głębokości. Jednak jest to zwykle zaimplementowane nie jako przeszukiwanie grafów, ale jako przeszukiwanie przypominające drzewo, które nie przechowuje tabeli osiągniętych stanów. Postęp poszukiwań ilustruje Rysunek; wyszukiwanie przechodzi natychmiast do najgłębszego poziomu drzewa wyszukiwania, gdzie węzły nie mają następców. Wyszukiwanie następnie „cofa się” do następnego najgłębszego węzła, który wciąż ma nierozwiniętych następców. Wyszukiwanie w głąb nie jest optymalne pod względem kosztów; zwraca pierwsze znalezione rozwiązanie, nawet jeśli nie jest najtańsze.

Kilkanaście kroków (od lewej do prawej, od góry do dołu) w trakcie przeszukiwania w głąb drzewa binarnego od stanu początkowego A do celu M. Granica jest zielona, z trójkątem oznaczającym węzeł, który ma zostać rozwinięty w następnej kolejności. Poprzednio rozwinięte węzły są lawendowe, a

potencjalne przyszłe węzły mają delikatne przerywane linie. Rozszerzone węzły bez potomków na granicy (bardzo słabe linie) można odrzucić.

Dla skończonych przestrzeni stanów, które są drzewami, jest wydajny i kompletny; w przypadku acyklicznych przestrzeni stanów może skończyć się wielokrotnym rozszerzaniem tego samego stanu różnymi ścieżkami, ale (ewentualnie) systematycznie bada całą przestrzeń. W cyklicznych przestrzeniach stanów może utknąć w nieskończonej pętli; dlatego niektóre implementacje wyszukiwania w głąb sprawdzają każdy nowy węzeł pod kątem cykli. Wreszcie, w nieskończonych przestrzeniach stanów przeszukiwanie w głąb nie jest systematyczne: może utknąć w nieskończonej ścieżce, nawet jeśli nie ma cykli. W związku z tym wyszukiwanie w głąb jest niekompletne. Przy tych wszystkich złych wiadomościach, dlaczego ktokolwiek miałby rozważać korzystanie z wyszukiwania w głąb, a nie wszerz lub w pierwszej kolejności? Odpowiedź jest taka, że ​​w przypadku problemów, w których możliwe jest wyszukiwanie podobne do drzewa, wyszukiwanie w głąb ma znacznie mniejsze zapotrzebowanie na pamięć. W ogóle nie trzymamy ustalonego stołu, a granica jest bardzo mała: pomyśl o granicy w przeszukiwaniu wszerz jako powierzchni stale rozszerzającej się sfery, podczas gdy granica w przeszukiwaniu w głąb to tylko promień kula.

W przypadku skończonej przestrzeni stanów w kształcie drzewa, przeszukiwanie drzewa w głąb najpierw zajmuje czas proporcjonalny do liczby stanów i ma złożoność pamięci tylko O(b,m) , gdzie b jest czynnikiem rozgałęzienia a m jest maksymalną głębokością drzewo. Niektóre problemy, które wymagałyby eksabajtów pamięci przy przeszukiwaniu wszerz, można rozwiązać przy użyciu tylko kilobajtów przy użyciu przeszukiwania w głąb. Ze względu na oszczędne wykorzystanie pamięci, przeszukiwanie drzewa w głąb zostało przyjęte jako podstawowy koń pociągowy wielu obszarów sztucznej inteligencji, w tym spełniania ograniczeń, spełnialności zdań  i programowania logicznego.

Wariant wyszukiwania w głąb, zwany wyszukiwaniem wstecznym, zużywa jeszcze mniej pamięci. Każdy częściowo rozwinięty węzeł zapamiętuje, który następnik wygenerować jako następny. Ponadto następniki są generowane przez bezpośrednią modyfikację opisu stanu bieżącego zamiast przydzielania pamięci dla zupełnie nowego stanu. Zmniejsza to wymagania dotyczące pamięci do tylko jednego opisu stanu i ścieżki działań O(m); znaczne oszczędności w stosunku do stanów O(bm) w przypadku wyszukiwania w głąb. W przypadku wycofywania mamy również możliwość utrzymywania wydajnej struktury danych dla stanów na bieżącej ścieżce, co pozwala nam na sprawdzanie ścieżki cyklicznej w czasie O(1), a nie O(m). Aby cofanie zadziałało, musimy być w stanie cofnąć każdą akcję, gdy się cofamy. . Cofanie się ma kluczowe znaczenie dla powodzenia wielu problemów z dużymi opisami stanów, takich jak montaż robotów.

Gdy akcje mają różne koszty, oczywistym wyborem jest użycie wyszukiwania „najlepszy-pierwszy”, gdzie funkcją oceny jest koszt ścieżki od korzenia do bieżącego węzła. Nazywa się to algorytmem Dijkstry przez społeczność informatyki teoretycznej i wyszukiwaniem jednolitych kosztów przez społeczność AI. Pomysł polega na tym, że podczas gdy wyszukiwanie wszerz rozprzestrzenia się falami o jednakowej głębokości, najpierw głębokości 1, potem głębokości 2, a zatem wyszukiwanie według jednolitego kosztu rozprzestrzenia się falami o jednakowych kosztach ścieżki. Algorytm może być zaimplementowany jako wywołanie BEST-FIRSTSEARCH z PATH-COST jako funkcją oceny.

Rozważmy rysunek , gdzie problemem jest dostanie się z Sibiu do Bukaresztu. Następcami Sibiu są Rimnicu Vilcea i Fagaras, z kosztami odpowiednio 80 i 99. Węzeł o najniższym koszcie, Rimnicu Vilcea, jest następnie rozbudowywany, dodając Pitesti z kosztem 80 = 97 = 177 .Węzeł o najniższym koszcie to teraz Fagaras, więc jest rozwijany, dodając Bukareszt z kosztem  99 + 211 = 310.Bukareszt jest celem, ale algorytm testuje cele tylko wtedy, gdy rozwija węzeł , a nie wtedy, gdy generuje węzeł, więc nie wykrył jeszcze, że jest to ścieżka do celu.

Algorytm kontynuuje, wybierając Pitesti jako następną ekspansję i dodając drugą ścieżkę do Bukaresztu z kosztem 80 + 97 + 101 = 278. Ma niższy koszt, więc zastępuje poprzednią ścieżkę w osiągniętym i jest dodawany do granicy. Okazuje się, że ten węzeł ma teraz najniższy koszt, więc jest uważany za następny, uznany za cel i zwrócony. Zauważ, że gdybyśmy sprawdzili cel przy generowaniu węzła, a nie podczas rozwijania węzła o najniższym koszcie, zwrócilibyśmy ścieżkę o wyższym koszcie (tę przez Fagarasa). Złożoność wyszukiwania o jednolitym koszcie jest scharakteryzowana C^* w kategoriach kosztu optymalnego rozwiązania a ϵ  dolnego ograniczenia kosztu każdego działania, przy czym ϵ > 0 Najgorsza złożoność czasowa i przestrzenna algorytmu jest znacznie większa niż b^d. Tak jest ponieważ wyszukiwanie o jednolitym koszcie może eksplorować duże drzewa działań o niskich kosztach przed zbadaniem ścieżek wiążących się z kosztownymi i być może użytecznymi działaniami. Gdy wszystkie koszty działań są równe to  b^d+1, przeszukiwanie jest sprawiedliwe i o jednolitym koszcie jest podobne do przeszukiwania wszerz. Wyszukiwanie o jednolitym koszcie jest kompletne i optymalne pod względem kosztów, ponieważ pierwsze znalezione rozwiązanie będzie miało koszt co najmniej tak niski, jak koszt każdego innego węzła na granicy. Wyszukiwanie o jednolitym koszcie systematycznie analizuje wszystkie ścieżki w kolejności rosnących kosztów, nigdy nie dając się złapać na jednej nieskończonej ścieżce (przy założeniu, że wszystkie koszty działania wynoszą > ϵ > 0 ).

Gdy wszystkie działania mają ten sam koszt, odpowiednią strategią jest przeszukiwanie wszerz, w którym najpierw rozwijany jest węzeł główny, następnie rozwijane są wszystkie następniki węzła głównego, następnie ich następcy i tak dalej. Jest to strategia systematycznego wyszukiwania, która jest zatem kompletna nawet w nieskończonych przestrzeniach stanów. Moglibyśmy zaimplementować wyszukiwanie wszerz jako wywołanie BEST-FIRST-SEARCH, gdzie funkcja oceny f(n) jest głębokością węzła — to znaczy liczbą działań, jakie trzeba wykonać, aby dotrzeć do węzła. Możemy jednak uzyskać dodatkową wydajność za pomocą kilku sztuczek. Kolejka typu pierwszy-w-pierwszy-wyszła będzie szybsza niż kolejka priorytetowa i da nam prawidłową kolejność węzłów: nowe węzły (które zawsze znajdują się głębiej niż ich rodzice) idą na tył kolejki, a stare węzły, które są płytsze niż nowe węzły, należy je najpierw rozszerzyć. Ponadto osiągnięty może być zbiór stanów, a nie mapowanie ze stanów na węzły, ponieważ po osiągnięciu stanu nigdy nie możemy znaleźć lepszej ścieżki do stanu. Oznacza to również, że możemy wykonać test wczesnego celu, sprawdzający, czy węzeł jest rozwiązaniem zaraz po jego wygenerowaniu, a nie test późnego celu, którego używa wyszukiwanie „najlepszy-pierwszy”, czekając, aż węzeł zostanie usunięty z kolejki. Rysunek przedstawia postęp w przeszukiwaniu wszerz w drzewie binarnym, a algorytm przedstawia algorytm z ulepszeniami wydajności wczesnego celu.

Wyszukiwanie wszerz zawsze znajduje rozwiązanie z minimalną liczbą akcji, ponieważ podczas generowania węzłów na głębokości d wygenerowało już wszystkie węzły na głębokości d-1, więc gdyby jeden z nich był rozwiązaniem, zostałoby znalezione. Oznacza to, że jest optymalny pod względem kosztów w przypadku problemów, w których wszystkie działania mają ten sam koszt, ale nie w przypadku problemów, które nie mają tej właściwości. W obu przypadkach jest kompletny. Pod względem czasu i przestrzeni wyobraź sobie poszukiwanie jednolitego drzewa, w którym każde państwo ma następców. Korzeń drzewa wyszukiwania generuje b węzłów, z których każdy generuje więcej węzłów, łącznie na drugim poziomie b². Każdy z nich generuje więcej węzłów, dając b³węzły na trzecim poziomie i tak dalej. Załóżmy teraz, że rozwiązanie znajduje się na głębokości d. Wtedy łączna liczba wygenerowanych węzłów wynosi

Wszystkie węzły pozostają w pamięci, więc zarówno czasowa, jak i przestrzenna złożoność O(b^d) są wykładniczymi ograniczeniami, które są przerażające. Jako typowy przykład ze świata rzeczywistego rozważ problem z szybkością przetwarzania współczynnika b = 10, rozgałęzienia 1 milion węzłów na sekundę i wymaganiami dotyczącymi pamięci 1 KB/węzeł. Wyszukiwanie do głębokości d = 10 zajęłoby mniej niż 3 godziny, ale wymagałoby 10 terabajtów pamięci. Wymagania dotyczące pamięci stanowią większy problem dla wyszukiwania wszerz niż czas wykonania. Ale czas jest nadal ważnym czynnikiem. Na głębokości d = 14, nawet przy nieskończonej pamięci, poszukiwania zajęłyby 3,5 roku. Ogólnie, problemów związanych z wyszukiwaniem złożoności wykładniczej nie można rozwiązać przez niedoinformowane wyszukiwanie jakichkolwiek przypadków poza najmniejszymi.

Niedoinformowany algorytm wyszukiwania nie ma pojęcia, jak blisko celu (celów) znajduje się stan. Weźmy na przykład naszego agenta w Arad, którego celem jest dotarcie do Bukaresztu. Niedoinformowany agent bez znajomości geografii Rumunii nie ma pojęcia, czy lepszym pierwszym krokiem jest wyjazd do Zerind czy Sibiu. W przeciwieństwie do tego, poinformowany agent (sekcja 3.5), który zna lokalizację każdego miasta, wie, że Sybin jest znacznie bliżej Bukaresztu, a zatem jest bardziej prawdopodobne, że znajduje się na najkrótszej ścieżce.