Miesiąc: sierpień 2021

Widzieliśmy, że jednym ze sposobów wymyślenia heurystyki jest wymyślenie zrelaksowanego problemu, dla którego można łatwo znaleźć optymalne rozwiązanie. Alternatywą jest uczenie się na doświadczeniu. „Doświadczenie” oznacza tutaj na przykład rozwiązywanie wielu 8-zagadek. Każde optymalne rozwiązanie.

Zadanie 8-zagadkowe dostarcza przykładowej pary (cel, ścieżka). Na podstawie tych przykładów algorytm uczenia może być użyty do skonstruowania funkcji, która może (przy odrobinie szczęścia) przybliżyć rzeczywisty koszt ścieżki dla innych stanów, które pojawiają się podczas wyszukiwania. Większość z tych podejść uczy się niedoskonałego przybliżenia funkcji heurystycznej, a tym samym ryzykuje niedopuszczalność. Prowadzi to do nieuniknionego kompromisu między czasem nauki, czasem wykonywania wyszukiwania i kosztem rozwiązania. Techniki uczenia maszynowego przedstawiono w rozdziale 19 . Metody uczenia się przez wzmacnianie opisane w rozdziale 22 mają również zastosowanie do wyszukiwania. Niektóre techniki uczenia maszynowego działają lepiej, gdy są dostarczane z funkcjami stanu, które są istotne dla przewidywania wartości heurystycznej stanu, a nie tylko z surowym opisem stanu. Na przykład funkcja „liczba niewłaściwie umieszczonych kafelków” może być pomocna w przewidywaniu rzeczywistej odległości stanu 8-puzzli od celu. Nazwijmy tę funkcję x₁(n).

Moglibyśmy wziąć 100 losowo wygenerowanych 8-zagadkowych konfiguracji i zebrać statystyki dotyczące ich rzeczywistych kosztów rozwiązania. Możemy stwierdzić, że gdy x₁(n) wynosi 5, średni koszt rozwiązania wynosi około 14 i tak dalej. Oczywiście możemy korzystać z wielu funkcji. Drugą cechą x₂(n) może być „liczba par sąsiednich płytek, które nie sąsiadują ze sobą w stanie docelowym”. Jak należy połączyć x₁(n) i x₂(n), aby przewidzieć h(n)? Powszechnym podejściem jest użycie kombinacji liniowej:

Stałe c1 i c2 są dostosowywane, aby zapewnić najlepsze dopasowanie do rzeczywistych danych w losowo generowanych konfiguracjach. Oczekuje się, że zarówno c1 jak i c2 będą dodatnie, ponieważ źle ułożone płytki i nieprawidłowe sąsiednie pary utrudniają rozwiązanie problemu. Zauważ, że ta heurystyka spełnia warunek h(n) = 0 dla stanów celu, ale niekoniecznie jest to dopuszczalne lub spójne.

Przedstawiliśmy kilka ustalonych strategii wyszukiwania — od szerokości do pierwszego, A* itd. — które zostały starannie zaprojektowane i zaprogramowane przez informatyków. Czy agent mógłby nauczyć się lepiej wyszukiwać? Odpowiedź brzmi tak, a metoda opiera się na ważnej koncepcji zwanej przestrzenią stanów metapoziomu. Każdy stan w metapoziomowej przestrzeni stanów przechwytuje wewnętrzny (obliczeniowy) stan programu, który przeszukuje zwykłą przestrzeń stanów, taką jak mapa Rumunii. (Aby oddzielić te dwa pojęcia, mapę Rumunii nazywamy przestrzenią stanów na poziomie obiektu). Na przykład stan wewnętrzny algorytmu A* składa się z bieżącego drzewa poszukiwań. Każda akcja w przestrzeni stanów metapoziomu jest krokiem obliczeniowym, który zmienia stan wewnętrzny; na przykład każdy krok obliczeń w A* rozwija węzeł liścia i dodaje jego następniki do drzewa. Tak więc Rysunek 3.18, który pokazuje sekwencję coraz większych drzew wyszukiwania, może być postrzegany jako obraz przedstawiający ścieżkę w przestrzeni stanów metapoziomu, gdzie każdy stan na ścieżce jest drzewem wyszukiwania na poziomie obiektu. W przypadku trudniejszych problemów będzie wiele takich błędnych kroków, a algorytm uczenia się na metapoziomie może uczyć się na tych doświadczeniach, aby uniknąć odkrywania mało obiecujących poddrzew. Techniki stosowane do tego rodzaju uczenia się zostały opisane w rozdziale później. Celem nauki jest zminimalizowanie całkowitego kosztu rozwiązywania problemów, kompensowanie kosztów obliczeniowych i kosztów ścieżki.

Istnieją usługi online, które udostępniają mapy z dziesiątkami milionów wierzchołków i znajdują optymalne pod względem kosztów wskazówki dojazdu w milisekundach. Jak mogą to zrobić, skoro najlepsze algorytmy wyszukiwania, które do tej pory rozważaliśmy, są około milion razy wolniejsze? Istnieje wiele sztuczek, ale najważniejszą z nich jest wstępne obliczenie niektórych optymalnych kosztów ścieżki. Chociaż wstępne obliczenia mogą być czasochłonne, należy je wykonać tylko raz, a następnie można je amortyzować przez miliardy żądań wyszukiwania użytkowników.

Moglibyśmy wygenerować idealną heurystykę, wstępnie obliczając i przechowując koszt optymalnej ścieżki między każdą parą wierzchołków. Zajęłoby to przestrzeń O(|V|²) i czas O(|E|³) – praktyczne dla grafów z 10 tysiącami wierzchołków, ale nie z 10 milionami. Lepszym podejściem jest wybranie kilku (być może 10 lub 20) punktów orientacyjnych z wierzchołków. Następnie dla każdego punktu orientacyjnego L i dla każdego innego wierzchołka na wykresie obliczamy i przechowujemy C*(v,L) dokładny koszt optymalnej ścieżki od v do L. (Potrzebujemy również na C*(L,v); graf nieskierowany to to samo, co C*(v,L) na grafie skierowanym—np. z ulicami jednokierunkowymi—musimy to obliczyć osobno.) Mając zapisane tabele C*, możemy łatwo stworzyć wydajną ( chociaż niedopuszczalne) heurystyka: minimalny koszt dotarcia z bieżącego węzła do punktu orientacyjnego, a następnie do celu, ponad wszystkimi punktami orientacyjnymi:

Jeśli optymalna ścieżka przechodzi przez punkt orientacyjny, ta heurystyka będzie dokładna; jeśli nie, to jest niedopuszczalne – zawyża koszt do celu. W wyszukiwaniu A*, jeśli masz dokładną heurystykę, to po dotarciu do węzła, który znajduje się na optymalnej ścieżce, każdy węzeł, który rozwiniesz od tego momentu, będzie na optymalnej ścieżce. Pomyśl o liniach konturowych jako podążających wzdłuż tej optymalnej ścieżki. Wyszukiwanie będzie przebiegać wzdłuż optymalnej ścieżki, w każdej iteracji dodając akcję z kosztem, aby uzyskać wynik, którego wartość będzie mniejsza, co oznacza, że ​​całkowity wynik f = g + h pozostanie stały na C* na całej ścieżce . Niektóre algorytmy wyszukiwania tras oszczędzają jeszcze więcej czasu, dodając skróty – sztuczne krawędzie na wykresie, które definiują optymalną ścieżkę wielu działań. Na przykład, gdyby istniały wstępnie zdefiniowane skróty między wszystkimi 100 największymi miastami w Stanach Zjednoczonych, a my próbowaliśmy nawigować z kampusu Berkeley w Kalifornii do NYU w Nowym Jorku, moglibyśmy skorzystać ze skrótu między Sacramento a Manhattanem i objąć 90% ścieżka w jednej akcji.

h_L(n) jest skuteczny, ale niedopuszczalny. Ale z większą ostrożnością możemy wymyślić heurystykę, która jest zarówno skuteczna, jak i dopuszczalna:

Nazywa się to heurystyką różniczkową (z powodu odejmowania). Pomyśl o tym z punktem orientacyjnym, który znajduje się gdzieś poza celem. Jeśli cel znajduje się na optymalnej ścieżce od n do punktu orientacyjnego, oznacza to: „rozważ całą ścieżkę od n do L, a następnie odejmij ostatnią część tej ścieżki, od celu do L, dając nam dokładny koszt ścieżka od n do celu.” Do tego stopnia, że ​​cel jest nieco poza optymalną ścieżką do punktu orientacyjnego, heurystyka będzie niedokładna, ale nadal dopuszczalna. Punkty orientacyjne, które nie znajdują się poza celem, nie będą przydatne; punkt orientacyjny, który znajduje się dokładnie w połowie drogi między n a celem, da h_DH = 0, co nie jest pomocne. Istnieje kilka sposobów na wybranie punktów orientacyjnych. Losowe wybieranie punktów jest szybkie, ale lepsze wyniki uzyskujemy, jeśli zadbamy o rozmieszczenie punktów orientacyjnych, aby nie znajdowały się zbyt blisko siebie. Chciwym podejściem jest losowe wybranie pierwszego punktu orientacyjnego, a następnie znalezienie punktu, który jest najbardziej od niego oddalony, dodanie go do zestawu punktów orientacyjnych i kontynuowanie w każdej iteracji + dodanie punktu, który maksymalizuje odległość do najbliższy punkt orientacyjny. Jeśli masz dzienniki wcześniejszych żądań wyszukiwania przez użytkowników, możesz wybrać punkty orientacyjne, które są często wymagane w wyszukiwaniach. W przypadku heurystyki różnicowej dobrze jest, jeśli punkty orientacyjne są rozmieszczone na obwodzie wykresu. Tak więc dobrą techniką jest znalezienie środka ciężkości wykresu, ułożenie klinów w kształcie koła wokół środka ciężkości, aw każdym klinie wybranie wierzchołka, który jest najdalej od środka. Punkty orientacyjne sprawdzają się szczególnie dobrze w problemach ze znajdowaniem tras ze względu na sposób rozmieszczenia dróg na świecie: duży ruch faktycznie chce podróżować między punktami orientacyjnymi, więc inżynierowie budowlani budują najszersze i najszybsze drogi wzdłuż tych tras; wyszukiwanie punktów orientacyjnych ułatwia odzyskanie tych tras.

Dopuszczalne heurystyki można również wyprowadzić z kosztu rozwiązania podproblemu danego problemu. Na przykład rysunek 3 podproblem instancji 8-puzzli . Podproblem polega na umieszczeniu płytek 1, 2, 3, 4 i półwyrobu we właściwych pozycjach. Oczywiście koszt optymalnego rozwiązania tego podproblemu jest dolną granicą kosztu całego problemu. W niektórych przypadkach okazuje się to dokładniejsze niż odległość Manhattanu.

Ideą baz danych wzorców jest przechowywanie tych dokładnych kosztów rozwiązania dla każdego możliwego wystąpienia podproblemu – w naszym przykładzie, każdej możliwej konfiguracji czterech płytek i pustego miejsca. (W bazie danych będzie 9 x8x7 x 6 x 5 = 15 120 wzorców. Tożsamości pozostałych czterech płytek są nieistotne dla celów rozwiązania podproblemu, ale ruchy tych płytek wliczają się do kosztu rozwiązania podproblemu.) Następnie obliczamy dopuszczalną heurystyczną bazę hdDB dla każdego stanu napotkanego podczas wyszukiwania, po prostu wyszukując odpowiednią konfigurację podproblemu w bazie danych. Sama baza danych jest konstruowana poprzez wyszukiwanie wstecz od celu i rejestrowanie kosztu każdego nowego napotkanego wzorca; koszt tych poszukiwań jest amortyzowany w kolejnych wystąpieniach problemów, a więc ma sens, jeśli oczekujemy, że zostaniemy poproszeni o rozwiązanie wielu problemów. Wybór płytek 1-2-3-4 pasujących do blanku jest dość arbitralny; moglibyśmy również skonstruować bazy danych dla 5-6-7-8, dla 2-4-6-8 i tak dalej. Każda baza danych daje dopuszczalną heurystykę, a te heurystyki można łączyć, jak wyjaśniono wcześniej, przyjmując maksymalną wartość. Połączona heurystyka tego rodzaju jest znacznie dokładniejsza niż odległość Manhattanu; liczba węzłów generowanych podczas rozwiązywania przypadkowych 15-zagadek może zostać zmniejszona o współczynnik 1000. Jednak z każdą dodatkową bazą danych maleją zyski i rosną koszty pamięci i obliczeń. Można się zastanawiać, czy można dodać heurystyki uzyskane z bazy danych 1-2-3-4 i 5-6-7-8, ponieważ te dwa podproblemy wydają się nie pokrywać. Czy to nadal dałoby dopuszczalną heurystykę? Odpowiedź brzmi nie, ponieważ rozwiązania podproblemu 1-2-3-4 i podproblemu 5-6-7-8 dla danego stanu prawie na pewno podzielą niektóre ruchy – jest mało prawdopodobne, aby 1-2-3-4 można przenieść na miejsce bez dotykania 5-6-7-8 i na odwrót. Ale co, jeśli nie liczymy tych ruchów – co, jeśli nie abstrahujemy pozostałych płytek do gwiazd, ale raczej sprawimy, że znikną? Oznacza to, że rejestrujemy nie całkowity koszt rozwiązania podproblemu 1-2-3-4, ale tylko liczbę ruchów obejmujących 1-2-3-4. Wtedy suma tych dwóch kosztów jest nadal dolną granicą kosztu rozwiązania całego problemu. To jest idea rozłącznych baz danych wzorców. Dzięki takim bazom danych możliwe jest rozwiązywanie przypadkowych 15-zagadek w ciągu kilku milisekund — liczba generowanych węzłów jest zmniejszona o współczynnik 10 000 w porównaniu z wykorzystaniem odległości Manhattan. W przypadku 24 zagadek można uzyskać przyspieszenie rzędu miliona. Rozłączne bazy danych wzorców sprawdzają się w przypadku łamigłówek z przesuwanymi płytkami, ponieważ problem można podzielić w taki sposób, że każdy ruch wpływa tylko na jeden podproblem – ponieważ tylko jedna płytka jest przesuwana na raz.

Widzieliśmy, że zarówno h₁ (niewłaściwie umieszczone kafelki), jak i h₂ (odległość Manhattanu) są całkiem dobrą heurystyką dla 8-puzzli i że h₂ jest lepsze. Jak można wymyślić h₂? Czy komputer może wymyślić taką heurystykę mechanicznie? h₁ i h₂ są szacunkowymi pozostałymi długościami ścieżki dla 8-puzzli, ale są również idealnie dokładnymi długościami ścieżek dla uproszczonych wersji układanki. Gdyby zasady łamigłówki zostały zmienione tak, aby płytka mogła się przesunąć w dowolne miejsce, a nie tylko do sąsiedniego pustego pola, to h₁ dałoby dokładną długość najkrótszego rozwiązania. Podobnie, gdyby płytka mogła przesunąć się o jedno pole w dowolnym kierunku, nawet na zajęte pole, to h₂ dałoby dokładną długość najkrótszego rozwiązania. Problem z mniejszymi ograniczeniami w działaniach nazywany jest zrelaksowanym problemem. Graf w przestrzeni stanów rozluźnionego problemu jest supergrafem oryginalnej przestrzeni stanów, ponieważ usunięcie ograniczeń tworzy dodatkowe krawędzie w grafie.

Ponieważ zrelaksowany problem dodaje krawędzie do grafu w przestrzeni stanów, każde optymalne rozwiązanie w pierwotnym problemie jest z definicji również rozwiązaniem w zrelaksowanym problemie; ale rozluźniony problem może mieć lepsze rozwiązania, jeśli dodane krawędzie zapewniają skróty. Stąd koszt optymalnego rozwiązania rozluźnionego problemu jest dopuszczalną heurystyką dla pierwotnego problemu. Ponadto, ponieważ pochodna heurystyka jest dokładnym kosztem rozwiązania problemu rozluźnionego, musi być zgodna z nierównością trójkąta i dlatego jest spójna . Jeśli definicja problemu jest napisana w języku formalnym, możliwe jest automatyczne konstruowanie zrelaksowanych problemów. Na przykład, jeśli akcje 8-puzzli są opisane jako

Płytka może przesunąć się z kwadratu X na kwadrat Y, jeśli

X sąsiaduje z Y, a Y jest puste,

możemy wygenerować trzy rozluźnione problemy, usuwając jeden lub oba warunki:

1. Płytka może przesunąć się z pola X na pole Y, jeśli X sąsiaduje z Y.
2. Płytka może przesunąć się z pola X do pola Y, jeśli Y jest puste.
3. Płytka może przesunąć się z pola X do pola Y.

Z (a) możemy wyprowadzić h₂ (odległość Manhattanu). Rozumowanie jest takie, że h₂ byłoby właściwym wynikiem, gdybyśmy przesunęli po kolei każdą płytkę do miejsca przeznaczenia. Z (c) możemy wyprowadzić h₁ (niewłaściwie umieszczone płytki), ponieważ byłby to właściwy wynik, gdyby płytki mogły przemieścić się do zamierzonego miejsca w jednej akcji. Zauważ, że bardzo ważne jest, aby rozluźnione problemy generowane przez tę technikę można było rozwiązać zasadniczo bez wyszukiwania, ponieważ rozluźnione reguły pozwalają rozłożyć problem na osiem niezależnych podproblemów. Jeśli zrelaksowany problem jest trudny do rozwiązania, wtedy uzyskanie wartości odpowiedniej heurystyki będzie kosztowne. Program o nazwie ABSOLVER może automatycznie generować heurystyki z definicji problemów, używając metody „rozluźnionego problemu” i różnych innych technik. ABSOLVER wygenerował nową heurystykę dla 8-zagadek, która była lepsza niż jakakolwiek wcześniejsza heurystyka i znalazł pierwszą przydatną heurystykę dla słynnej układanki z kostką Rubika. Jeśli dla problemu dostępny jest zbiór dopuszczalnych heurystyk h₁…h_m i żadna z nich nie jest wyraźnie lepsza od pozostałych, co powinniśmy wybrać? Jak się okazuje, możemy mieć to, co najlepsze ze wszystkich światów, definiując

h(n) = max{h₁(n),…, h_k(n)}

Ta złożona heurystyka wybiera tę funkcję, która jest najdokładniejsza w danym węźle. Ponieważ składniki hi są dopuszczalne, jest dopuszczalne (a jeśli wszystkie hi są spójne, to h jest zgodne). Co więcej, h dominuje nad wszystkimi heurystykami składowymi. Jedyną wadą jest h(n), której obliczenie zajmuje więcej czasu. Jeśli jest to problem, alternatywą jest losowy wybór jednej z heurystyk przy każdej ocenie lub użycie algorytmu uczenia maszynowego, aby przewidzieć, która heurystyka będzie najlepsza. Takie postępowanie może skutkować niespójną heurystyką (nawet jeśli każde hi jest spójne), ale w praktyce zwykle prowadzi to do szybszego rozwiązywania problemów.

Przyjrzymy się, jak dokładność heurystyki wpływa na wydajność wyszukiwania, a także rozważymy, jak można wymyślić heurystykę. Jako nasz główny przykład powrócimy do 8-zagadki. Jak wspomniano w Sekcji 3.2, celem łamigłówki jest przesuwanie płytek poziomo lub pionowo w pustą przestrzeń, aż konfiguracja będzie pasować do konfiguracji celu.

W 8 Puzzle jest 9!/2 = 181 400 osiągalnych stanów, więc wyszukiwanie może z łatwością zachować je wszystkie w pamięci. Ale dla 15-puzzli jest 16!/2 stanów – ponad 10 bilionów – więc aby przeszukać tę przestrzeń, będziemy potrzebować pomocy dobrej, dopuszczalnej funkcji heurystycznej. Istnieje długa historia takich heurystyk dla 15-puzzli; oto dwa powszechnie używane kandydaci:

* h₁ = liczba zagubionych płytek (brak pustego miejsca). Na rysunku 3.25 wszystkie osiem płytek jest nie na miejscu, więc stan początkowy ma h₁ = 8, h₁ jest dopuszczalną heurystyką, ponieważ każda płytka, która jest nie na miejscu, będzie wymagała co najmniej jednego ruchu, aby umieścić ją we właściwym miejscu.

* h₂ = suma odległości płytek od ich pozycji bramkowych. Ponieważ kafelki nie mogą się poruszać po przekątnych, odległość jest sumą odległości poziomych i pionowych – czasami nazywanej odległością między miastami lub Manhattanem. h2 jest również dopuszczalne, ponieważ każdy ruch może zrobić, to przesunąć jedną płytkę o jeden krok bliżej celu. Kafelki od 1 do 8 w stanie początkowym na rysunku 3.25 dają odległość Manhattanu

h2 = 3 + 1 + 2 + 2 + 2 + 3 + 3 + 2 = 18.

Zgodnie z oczekiwaniami żadne z nich nie zawyża rzeczywistego kosztu rozwiązania, który wynosi 26.

3.6.1 Wpływ dokładności heurystycznej na wydajność

Jednym ze sposobów scharakteryzowania jakości heurystyki jest efektywny współczynnik rozgałęzienia b*. Jeśli całkowita liczba węzłów wygenerowanych przez A* dla konkretnego problemu wynosi N, a głębokość rozwiązania wynosi d, to b* jest współczynnikiem rozgałęzienia, który musiałoby mieć jednolite drzewo o głębokości d, aby zawierało N+1 węzłów. Zatem,

N + 1 = 1 + b^∗ + (b^∗)² +⋯+ (b^∗)^d.

Na przykład, jeśli A* znajdzie rozwiązanie na głębokości 5 przy użyciu 52 węzłów, to efektywny współczynnik rozgałęzienia wynosi 1,92. Efektywny współczynnik rozgałęzienia może się różnić w różnych instancjach problemów, ale zwykle dla określonej domeny (takiej jak 8-zagadek) jest dość stały we wszystkich nietrywialnych instancjach problemów. Dlatego eksperymentalne pomiary b^* na małym zestawie problemów mogą stanowić dobry przewodnik po ogólnej użyteczności heurystyki. Dobrze zaprojektowana heurystyka miałaby wartość b^* bliską 1, pozwalając na rozwiązanie dość dużych problemów przy rozsądnych kosztach obliczeniowych. Korf i Reid twierdzą, że lepszym sposobem scharakteryzowania efektu przycinania A^* przy użyciu danej heurystyki jest zmniejszenie głębokości efektywnej o stałą wartość k_h w porównaniu z głębokością rzeczywistą. Oznacza to, że całkowity koszt wyszukiwania wynosi O(b^d-kh) w porównaniu z O(b^d) w przypadku wyszukiwania bez informacji. Eksperymenty z kostką Rubika i problemami łamigłówkowymi pokazują, że ta formuła daje dokładne prognozy całkowitego kosztu wyszukiwania dla próbkowanych instancji problemów w szerokim zakresie długości rozwiązań – przynajmniej dla rozwiązań o długości większej niż k_h.

Dla rysunku wygenerowaliśmy losowe problemy z ośmioma łamigłówkami i rozwiązaliśmy je za pomocą niedoinformowanego przeszukiwania wszerz oraz przeszukiwania A* przy użyciu zarówno h₁ i h₂ podających średnią liczbę wygenerowanych węzłów i odpowiadający jej efektywny współczynnik rozgałęzienia dla każdej strategii wyszukiwania i dla każdej długości rozwiązania. Wyniki sugerują, że h₂ jest lepsze niż h₁ i oba są lepsze niż brak heurystyki.

Porównanie kosztów wyszukiwania i efektywnych współczynników rozgałęzienia dla problemów z 8 łamigłówkami przy użyciu szerokości na pierwszym miejscu

szukaj, A^* z

h₁

(zagubione płytki) i A^* z

h₂

(Odległość Manhattanu). Dane są uśredniane z ponad 100 puzzli dla każdej długości rozwiązania

d

od 6 do 28.

Można by zapytać, czy h₂ jest zawsze lepsze niż h₁. Odpowiedź brzmi: „Zasadniczo tak”. Łatwo zauważyć z definicji obu heurystyk, że dla dowolnego węzła n ,h₂(n) ≥ h1(n) Mówimy zatem, że h₂ dominuje nad h₁. Dominacja przekłada się bezpośrednio na efektywność: A* używający h₂ nigdy nie rozwinie więcej węzłów niż A^* używający h1 (poza przypadkowym zerwaniem więzi). Argument jest prosty. Przypomnij sobie obserwację, że każdy węzeł z f(n) < C* na pewno zostanie rozszerzony. To to samo, co powiedzenie, że każdy węzeł z h(n) < C* – g(n) jest na pewno rozwinięty, gdy jest niesprzeczny. Ale ponieważ h₂ jest co najmniej tak duże jak h₁ dla wszystkich węzłów, każdy węzeł, który z pewnością jest rozszerzany przez przeszukiwanie A* z h₂ jest również z pewnością rozszerzany z h₁ i może spowodować rozwinięcie innych węzłów. Dlatego generalnie lepiej jest użyć funkcji heurystycznej o wyższych wartościach, pod warunkiem, że jest ona spójna i czas obliczeń heurystyki nie jest zbyt długi.

W przypadku jednokierunkowego wyszukiwania typu „najlepszy-pierwszy” zauważyliśmy, że użycie  f(n) = g(n) + h(n) jako funkcji oceny daje nam przeszukiwanie A*, które gwarantuje znalezienie rozwiązań o optymalnym koszcie (przy założeniu dopuszczalnego ), a jednocześnie jest optymalnie wydajne pod względem liczby rozwiniętych węzłów. W przypadku dwukierunkowego wyszukiwania typu „najlepszy-pierwszy” moglibyśmy również spróbować użyć f(n) = g(n) + h(n)  , ale niestety nie ma gwarancji, że doprowadzi to do rozwiązania o optymalnych kosztach ani że będzie optymalnie wydajne, nawet przy dopuszczalnej heurystyce. Przy wyszukiwaniu dwukierunkowym okazuje się, że to nie pojedyncze węzły, ale raczej pary węzłów (po jednym z każdej granicy) można udowodnić, że są na pewno rozwinięte, więc każdy dowód wydajności będzie musiał uwzględniać pary węzłów. Zaczniemy od nowej notacji. Używamy f_F(n) = g_F(n) + h_F(n)  dla węzłów idących w przód (ze stanem początkowym jako root) oraz f_B(n) = g_B(n) + h_B(n)   dla węzłów w kierunku wstecznym (ze stanem docelowym jako root). Chociaż zarówno wyszukiwanie do przodu, jak i do tyłu rozwiązuje ten sam problem, mają różne funkcje oceny, ponieważ na przykład heurystyki różnią się w zależności od tego, czy dążysz do celu, czy do stanu początkowego. Założymy dopuszczalną heurystykę. Rozważ ścieżkę w przód od stanu początkowego do węzła m i ścieżkę powrotną od celu do węzła n. Możemy zdefiniować dolne ograniczenie kosztu rozwiązania, które podąża ścieżką od stanu początkowego do m następnie w jakiś sposób dociera do n , a następnie podąża ścieżką do celu jako

lb(m,n) =  max(gF(m) + gB(n),f_F(m),f_B(n)

 Innymi słowy, koszt takiej ścieżki musi być co najmniej tak duży, jak suma kosztów ścieżki obu części (ponieważ pozostałe połączenie między nimi musi mieć koszt nieujemny), a koszt również musi być co najmniej tyle, ile szacowany koszt każdej części (ponieważ szacunki heurystyczne są optymistyczne). Biorąc to pod uwagę, twierdzenie jest takie, że dla dowolnej pary węzłów (m,n)  z lb(m,n) o koszcie mniejszym niż optymalny C^*musimy rozszerzyć m albo n ponieważ ścieżka, która przechodzi przez oba z nich, jest potencjalnie optymalnym rozwiązaniem. Trudność polega na tym, że nie wiemy na pewno, który węzeł najlepiej rozwinąć, a zatem żaden algorytm wyszukiwania dwukierunkowego nie może zagwarantować, że będzie optymalnie wydajny – każdy algorytm może rozszerzyć do dwukrotności minimalnej liczby węzłów, jeśli zawsze wybierze złą składową pary, która ma się rozwinąć jako pierwsza. Niektóre algorytmy dwukierunkowego wyszukiwania heurystycznego wprost zarządzają kolejką par (m,n), ale pozostaniemy przy dwukierunkowym wyszukiwaniu „najlepszy-pierwszy”, które ma dwie kolejki priorytetów granicznych, i nadamy mu funkcję oceny, która naśladuje kryteria lb:

f₂(n) =  max(2g(n), g(n) + h(n)

Węzeł do rozwinięcia jako następny będzie tym, który minimalizuje tę wartość f₂ ; węzeł może pochodzić z dowolnej granicy. Ta funkcja f₂ gwarantuje, że nigdy nie rozszerzymy węzła (z którejkolwiek granicy) z g(n) > C^*/2. Mówimy, że dwie połowy wyszukiwania „spotykają się w środku” w tym sensie, że kiedy dwie granice się stykają, żaden węzeł wewnątrz żadnej z granic nie ma ścieżki koszt większy niż granica C^*/2. Rysunek przedstawia przykładowe wyszukiwanie dwukierunkowe.

Wyszukiwanie dwukierunkowe utrzymuje dwie granice: po lewej węzły A i B są następcami Start; po prawej węzeł F jest odwrotnym następcą celu. Każdy węzeł jest oznaczony wartościami f = g + h i wartością f₂ = max(2g, g + h) . (Wartości g są sumą kosztów działania, jak pokazano na każdej strzałce; wartości h  są arbitralne i nie można ich wyprowadzić z niczego na rysunku). Optymalne rozwiązanie, Start-A-Goal, ma koszt C^* = 4 + 2 + 4 = 10, co oznacza, że spotkanie- algorytm dwukierunkowy in-the-middle nie powinien rozszerzać żadnego węzła za pomocą g > C^*/2  =5 i rzeczywiście następnym węzłem do rozwinięcia będzie A lub F (każdy z g = 4 ), co prowadzi nas do optymalnego rozwiązania. Gdybyśmy najpierw rozszerzyli węzeł o najniższym koszcie, wtedy B i C byłyby następne, a D i E byłyby powiązane z A, ale wszystkie mają g > C^*/2   i dlatego nigdy nie są rozwijane, gdy f₂  jest funkcja oceny.

Opisaliśmy podejście, w którym heurystyka h_F szacuje odległość do celu (lub, gdy problem ma wiele stanów celu, odległość do najbliższego celu), a h_B szacuje odległość do początku. Nazywa się to wyszukiwaniem od frontu do końca. Alternatywa, zwana przeszukiwaniem front-to-front, polega na próbie oszacowania odległości do drugiej granicy. Oczywiście, jeśli granica ma miliony węzłów, nieefektywne byłoby zastosowanie funkcji heurystycznej do każdego z nich i przyjęcie minimum. Ale może działać próbkowanie kilku węzłów z granicy. W pewnych specyficznych dziedzinach problemowych możliwe jest podsumowanie granicy — na przykład w przypadku przeszukiwania siatki możemy przyrostowo obliczyć ramkę graniczną i użyć jako heurystyki odległość do ramki granicznej. Wyszukiwanie dwukierunkowe jest czasami bardziej wydajne niż wyszukiwanie jednokierunkowe, czasami nie. Ogólnie rzecz biorąc, jeśli mamy bardzo dobrą heurystykę, to wyszukiwanie A* tworzy kontury wyszukiwania, które są skoncentrowane na celu, a dodanie wyszukiwania dwukierunkowego niewiele pomaga. Przy przeciętnym heurystycznym wyszukiwaniu dwukierunkowym, które spotyka się w środku, ma tendencję do rozszerzania mniejszej liczby węzłów i jest preferowane. W najgorszym przypadku słabej heurystyki wyszukiwanie nie jest już skoncentrowane na celu, a wyszukiwanie dwukierunkowe ma taką samą asymptotyczną złożoność jak A*. Wyszukiwanie dwukierunkowe z funkcją oceny f₂ i dopuszczalną heurystyką jest kompletne i optymalne.

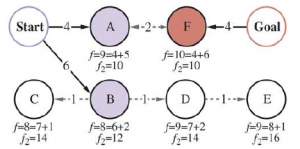
Głównym problemem z A* jest wykorzystanie pamięci. W tej sekcji omówimy kilka sztuczek implementacyjnych, które oszczędzają miejsce, a następnie kilka zupełnie nowych algorytmów, które lepiej wykorzystują dostępną przestrzeń. Pamięć jest podzielona między stany graniczne i osiągnięte. W naszej implementacji wyszukiwania best-first stan, który znajduje się na granicy, jest przechowywany w dwóch miejscach: jako węzeł na granicy (abyśmy mogli zdecydować, co dalej rozwinąć) oraz jako wpis w tabeli stanów osiągniętych (więc wiemy jeśli odwiedziliśmy ten stan wcześniej). W przypadku wielu problemów (takich jak eksploracja siatki) to powielanie nie stanowi problemu, ponieważ rozmiar granicy jest znacznie mniejszy niż osiągnięty, więc powielanie stanów na granicy wymaga stosunkowo niewielkiej ilości pamięci. Ale niektóre implementacje utrzymują stan tylko w jednym z dwóch miejsc, oszczędzając trochę miejsca kosztem komplikacji (i być może spowolnienia) algorytmu. Inną możliwością jest usunięcie stanów z osiągniętych, kiedy możemy udowodnić, że nie są już potrzebne. W przypadku niektórych problemów możemy użyć właściwości separacji (Rysunek 3.6 na stronie 72) wraz z zakazem wykonywania zawracania, aby upewnić się, że wszystkie działania przesuną się na zewnątrz z granicy lub do innego stanu granicznego. W takim przypadku wystarczy sprawdzić granicę pod kątem zbędnych ścieżek i możemy wyeliminować osiągniętą tabelę. W przypadku innych problemów możemy zachować liczniki odwołań wskazujące, ile razy stan został osiągnięty i usunąć go z osiągniętej tabeli, gdy nie ma więcej sposobów na osiągnięcie stanu. Na przykład w świecie z siatką, w którym każdy stan można osiągnąć tylko od czterech sąsiadów, po czterokrotnym osiągnięciu stanu możemy usunąć go z tabeli. Rozważmy teraz nowe algorytmy, które mają na celu oszczędzanie pamięci.

Wyszukiwanie wiązki ogranicza rozmiar granicy. Najprostszym podejściem jest zachowanie tylko węzłów z najlepszymi wynikami, odrzucając wszelkie inne rozwinięte węzły. To oczywiście sprawia, że ​​wyszukiwanie jest niekompletne i nieoptymalne, ale możemy zdecydować się na dobre wykorzystanie dostępnej pamięci, a algorytm działa szybko, ponieważ rozszerza mniej węzłów. W przypadku wielu problemów może znaleźć dobre, prawie optymalne rozwiązania. Możesz myśleć o przeszukiwaniu o jednolitym koszcie lub A* jako o rozchodzeniu się wszędzie w koncentrycznych konturach, a o przeszukiwaniu wiązką jako o badaniu tylko skupionej części tych konturów, części, która zawiera najlepszych kandydatów. Alternatywna wersja wyszukiwania wiązki nie utrzymuje ścisłego limitu rozmiaru granicy, ale zamiast tego utrzymuje każdy węzeł, którego -wynik mieści się w najlepszym -wyniku. W ten sposób, gdy istnieje kilka węzłów o silnej punktacji, tylko kilka zostanie zachowanych, ale jeśli nie ma żadnych silnych węzłów, zostanie zachowanych więcej, dopóki nie pojawi się silny.

Pogłębiające iteracyjne przeszukiwanie A* (IDA*) jest dla A* tym, czym iteracyjne-pogłębiające przeszukiwanie jest od pierwszego w głąb: IDA* daje nam korzyści z A* bez konieczności zachowywania w pamięci wszystkich osiągniętych stanów, kosztem odwiedzenia niektórych stanów wiele razy. Jest to bardzo ważny i powszechnie stosowany algorytm rozwiązywania problemów, które nie mieszczą się w pamięci. W standardowym pogłębianiu iteracyjnym odcięciem jest głębokość, która jest zwiększana o jedną w każdej iteracji. W IDA* punktem odcięcia jest koszt f ( g+h); w każdej iteracji wartość odcięcia jest najmniejszym kosztem dowolnego węzła, który przekroczył wartość odcięcia w poprzedniej iteracji. Innymi słowy , każda iteracja wyczerpująco przeszukuje -kontur, znajduje węzeł tuż za tym konturem i używa -kosztu tego węzła jako następnego konturu. W przypadku problemów, takich jak 8-puzzle, w których koszt każdej ścieżki jest liczbą całkowitą, działa to bardzo dobrze, powodując stały postęp w kierunku celu w każdej iteracji. Jeśli optymalne rozwiązanie kosztuje C* , to nie może być więcej niż C* iteracji (na przykład nie więcej niż 31 iteracji na najtrudniejszych 8-zagadkowych problemach). Ale w przypadku problemu, w którym każdy węzeł ma inny koszt f, każdy nowy kontur może zawierać tylko jeden nowy węzeł, a liczba iteracji może być równa liczbie stanów.

Rekurencyjne przeszukiwanie „najlepszy-pierwszy” (RBFS) próbuje naśladować działanie standardowego przeszukiwania „najlepszy-pierwszy”, ale używa tylko przestrzeni liniowej.

RBFS przypomina rekurencyjne wyszukiwanie wgłębne, ale zamiast kontynuować w nieskończoność bieżącą ścieżkę, używa zmiennej _limit do śledzenia wartości f najlepszej alternatywnej ścieżki dostępnej od dowolnego przodka bieżącego węzła. Jeśli bieżący węzeł przekroczy ten limit, rekursja zostanie cofnięta do alternatywnej ścieżki. Gdy rekursja się rozwija, RBFS zastępuje wartość f każdego węzła na ścieżce wartością z kopii zapasowej — najlepszą wartością f jego dzieci. W ten sposób RBFS zapamiętuje wartość f najlepszego liścia w zapomnianym poddrzewie i dlatego może zdecydować, czy warto ponownie rozwinąć poddrzewo w późniejszym czasie. Rysunek  pokazuje, w jaki sposób RBFS dociera do Bukaresztu.

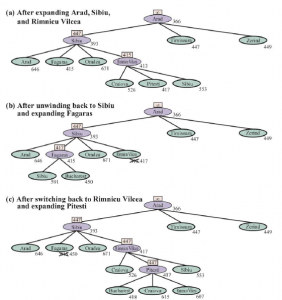
Etapy w RBFS szukają najkrótszej trasy do Bukaresztu. Wartość f-limit dla każdego wywołania rekurencyjnego jest pokazana na górze każdego bieżącego węzła, a każdy węzeł jest oznaczony swoim kosztem f. (a) Ścieżka przez Rimnicu Vilcea jest kontynuowana, aż aktualnie najlepszy liść (Pitesti) ma wartość gorszą niż najlepsza alternatywa Ath (Fagaras). (b) Rekurencja rozwija się i najlepsza wartość liścia zapomnianego poddrzewa (417) jest kopiowana do Rimnicu Vilcea; następnie Fagaras jest rozwijany, odsłaniając najlepszą wartość liścia wynoszącą 450. (c) Rekurencja rozwija się i najlepsza wartość liścia zapomnianego poddrzewa (450) jest kopiowana do Fagarasa; następnie rozbudowuje się Rimnicu Vilcea. Tym razem, ponieważ najlepsza alternatywna droga (przez Timisoarę) kosztuje co najmniej 447, ekspansja trwa dalej do Bukaresztu.

RBFS jest nieco bardziej wydajny niż IDA*, ale nadal cierpi z powodu nadmiernej regeneracji węzłów. W przykładzie na rysunku 3.23 RBFS podąża ścieżką przez Rimnicu Vilcea, następnie „zmienia zdanie” i próbuje Fagaras, a następnie ponownie zmienia zdanie. Te zmiany myślenia zachodzą, ponieważ za każdym razem, gdy bieżąca najlepsza ścieżka jest rozszerzana, jej wartość f prawdopodobnie wzrośnie — h jest zwykle mniej optymistyczny dla węzłów bliższych celowi. Kiedy tak się stanie, druga najlepsza ścieżka może stać się najlepszą ścieżką, więc poszukiwanie musi się cofnąć, aby nią podążać. Każda zmiana myślenia odpowiada iteracji IDA* i może wymagać wielu ponownych rozszerzeń zapomnianych węzłów, aby odtworzyć najlepszą ścieżkę i rozszerzyć ją o kolejny węzeł.

RBFS jest optymalny, jeśli dopuszczalna jest funkcja heurystyczna h(n). Jego złożoność przestrzenna jest liniowa na głębokości najgłębszego optymalnego rozwiązania, ale jego złożoność czasowa jest raczej trudna do scharakteryzowania: zależy ona zarówno od dokładności funkcji heurystycznej, jak i od tego, jak często zmienia się najlepsza ścieżka w miarę rozszerzania węzłów. Rozszerza węzły w kolejności rosnącej f -score, nawet jeśli f jest niemonotoniczne.

IDA* i RBFS cierpią z powodu używania zbyt małej ilości pamięci. Między iteracjami IDA* zachowuje tylko jedną liczbę: aktualny limit kosztów F. RBFS zachowuje więcej informacji w pamięci, ale wykorzystuje tylko przestrzeń liniową: nawet jeśli więcej pamięci byłoby dostępne, RBFS nie ma możliwości jej wykorzystania. Ponieważ zapominają o większości tego, co zrobili, oba algorytmy mogą w efekcie wielokrotnie ponownie badać te same stany. Rozsądne wydaje się zatem określenie, ile mamy dostępnej pamięci i umożliwienie algorytmowi wykorzystania jej całej. Dwa algorytmy, które to robią, to MA* (A* ograniczone do pamięci) i SMA* (uproszczone MA*). SMA* jest dużo prostsze, więc to opiszemy. SMA* postępuje podobnie jak A*, rozwijając najlepszy liść aż do zapełnienia pamięci. W tym momencie nie może dodać nowego węzła do drzewa wyszukiwania bez usunięcia starego. SMA* zawsze odrzuca najgorszy węzeł liścia — ten z najwyższą wartością f. Podobnie jak RBFS, SMA* następnie tworzy kopię zapasową wartości zapomnianego węzła do swojego rodzica. W ten sposób przodek zapomnianego poddrzewa zna jakość najlepszej ścieżki w tym poddrzewie. Dzięki tym informacjom SMA* regeneruje poddrzewo tylko wtedy, gdy wszystkie inne ścieżki wyglądają gorzej niż ścieżka, którą zapomniała. Innym sposobem powiedzenia tego jest to, że jeśli zapomnimy o wszystkich potomkach węzła n, to nie będziemy wiedzieć, w którą stronę przejść od n , ale nadal będziemy mieli wyobrażenie o tym, jak opłaca się iść gdziekolwiek od n. Cały algorytm jest opisany w internetowym repozytorium kodu dołączonym do tej książki. Warto wspomnieć o jednej subtelności. Powiedzieliśmy, że SMA* rozwija najlepszy liść i usuwa najgorszy liść. Co się stanie, jeśli wszystkie węzły liści mają tę samą wartość f? Aby uniknąć wybierania tego samego węzła do usunięcia i rozwinięcia, SMA* rozwija najnowszy najlepszy liść i usuwa najstarszy najgorszy liść. Są one zbieżne, gdy istnieje tylko jeden liść, ale w takim przypadku bieżące drzewo wyszukiwania musi być pojedynczą ścieżką od korzenia do liścia, która wypełnia całą pamięć. Jeśli liść nie jest węzłem celu, to nawet jeśli znajduje się na optymalnej ścieżce rozwiązania, rozwiązanie to nie jest osiągalne z dostępną pamięcią. Dlatego węzeł można odrzucić dokładnie tak, jakby nie miał następców. SMA* jest zakończona, jeśli istnieje jakiekolwiek osiągalne rozwiązanie, to znaczy, jeśli głębokość najpłytszego węzła docelowego jest mniejsza niż rozmiar pamięci (wyrażony w węzłach). Optymalne jest, jeśli osiągalne jest jakiekolwiek optymalne rozwiązanie; w przeciwnym razie zwraca najlepsze osiągalne rozwiązanie. W praktyce SMA* jest dość solidnym wyborem do znajdowania optymalnych rozwiązań, szczególnie gdy przestrzeń stanów jest grafem, koszty działania nie są jednolite, a generowanie węzłów jest drogie w porównaniu z kosztami utrzymania granicy i osiągniętego zbioru. Jednak w przypadku bardzo trudnych problemów często zdarza się, że SMA* jest zmuszony do ciągłego przełączania się między wieloma potencjalnymi ścieżkami rozwiązania, z których tylko mały podzbiór może zmieścić się w pamięci. (Przypomina to problem thrashingu w systemach stronicowania dysków.) Następnie dodatkowy czas wymagany do powtórnej regeneracji tych samych węzłów oznacza, że ​​problemy, które byłyby praktycznie możliwe do rozwiązania przez A* przy nieograniczonej ilości pamięci, stają się nie do rozwiązania dla SMA*. Innymi słowy, ograniczenia pamięci mogą sprawić, że problem będzie trudny do rozwiązania z punktu widzenia czasu obliczeń. Chociaż żadna aktualna teoria nie wyjaśnia kompromisu między czasem a pamięcią, wydaje się, że jest to nieunikniony problem. Jedynym wyjściem jest porzucenie wymogu optymalności.

Wyszukiwanie* ma wiele dobrych cech, ale rozszerza wiele węzłów. Możemy zbadać mniej węzłów (zabierając mniej czasu i przestrzeni), jeśli jesteśmy gotowi zaakceptować rozwiązania, które są nieoptymalne, ale są „wystarczająco dobre” – co nazywamy satysfakcjonującymi rozwiązaniami. Jeśli pozwolimy wyszukiwaniu A* na użycie niedopuszczalnej heurystyki — takiej, która może być przeszacowana — ryzykujemy pominięcie optymalnego rozwiązania, ale heurystyka może być potencjalnie bardziej dokładna, zmniejszając w ten sposób liczbę rozwiniętych węzłów. Na przykład inżynierowie drogowi znają pojęcie wskaźnika objazdu, który jest mnożnikiem stosowanym do odległości w linii prostej w celu uwzględnienia typowej krzywizny dróg. Wskaźnik objazdu wynoszący 1,3 oznacza, że ​​jeśli dwa miasta są oddalone od siebie o 10 mil w linii prostej, dobre oszacowanie najlepszej ścieżki między nimi wynosi 13 mil. Dla większości miejscowości wskaźnik objazdu waha się od 1,2 do 1,6. Możemy zastosować tę ideę do dowolnego problemu, nie tylko dotyczącego dróg, za pomocą podejścia zwanego przeszukiwaniem ważonym A*, w którym ważymy wartość heurystyczną bardziej, dając nam funkcję oceny f(n) = g(n) +W x h( n) dla niektórych W > 1. Rysunek pokazuje problem wyszukiwania w świecie siatki. W (a) wyszukiwanie A* znajduje optymalne rozwiązanie, ale aby je znaleźć, musi zbadać dużą część przestrzeni stanów. W (b) ważone wyszukiwanie A* znajduje rozwiązanie, które jest nieco droższe, ale czas wyszukiwania jest znacznie szybszy. Widzimy, że ważone wyszukiwanie skupia kontur osiągniętych stanów w kierunku celu. Oznacza to, że eksplorowanych jest mniej stanów, ale jeśli optymalna ścieżka kiedykolwiek wyjdzie poza kontur ważonego wyszukiwania (jak to ma miejsce w tym przypadku), to optymalna ścieżka nie zostanie znaleziona. Ogólnie rzecz biorąc, jeśli optymalne rozwiązanie kosztuje C* ważone wyszukiwanie A*, znajdzie rozwiązanie, które kosztuje gdzieś pomiędzy C^* a  W x C^*, ale w praktyce zwykle otrzymujemy wyniki znacznie bliższe C* niż W x C^*.

Dwa wyszukiwania na tej samej siatce: (a) wyszukiwanie A* i (b) wyszukiwanie ważone A* z wagą W = 2. Szare paski to przeszkody, fioletowa linia to ścieżka od zielonego startu do czerwonego celu, oraz małe kropki to stany osiągnięte podczas każdego wyszukiwania. W przypadku tego konkretnego problemu ważone A* bada 7 razy mniej stanów i znajduje ścieżkę, która jest o 5% droższa. Rozważaliśmy wyszukiwania, które oceniają stany przez łączenie i na różne sposoby; ważone A* można postrzegać jako uogólnienie pozostałych:

Wyszukiwanie A*: g(n) + h(n)  (W = 1)

Wyszukiwanie według jednolitych kosztów: g(n) (W = 0)

Chciwe wyszukiwanie najpierw: h(n) (W = ∞)

Wyszukiwanie ważone A*: g(n) +W x h(n) (1 < W  < ∞)

Możesz nazwać ważone A* „nieco zachłanne wyszukiwanie”: podobnie jak zachłanne wyszukiwanie „najlepiej-najpierw”, skupia ono wyszukiwanie na celu; z drugiej strony nie zignoruje całkowicie kosztu ścieżki i zawiesi ścieżkę, która robi niewielkie postępy wielkim kosztem. Istnieje wiele nieoptymalnych algorytmów wyszukiwania, które można scharakteryzować za pomocą kryteriów określających, co jest „wystarczająco dobre”. W ograniczonym wyszukiwaniu suboptymalnym szukamy rozwiązania, które gwarantuje, że mieści się w stałym współczynniku W kosztu optymalnego. Ważona A* zapewnia tę gwarancję. W wyszukiwaniu z kosztem ograniczonym szukamy rozwiązania, którego koszt jest mniejszy niż pewna stała C. A w wyszukiwaniu z kosztem nieograniczonym akceptujemy rozwiązanie o dowolnym koszcie, o ile możemy je szybko znaleźć. Przykładem algorytmu wyszukiwania o nieograniczonych kosztach jest szybkie wyszukiwanie, które jest wersją zachłannego wyszukiwania „najlepiej najpierw”, które wykorzystuje jako heurystykę szacowaną liczbę działań wymaganych do osiągnięcia celu, niezależnie od kosztu tych działań. Tak więc w przypadku problemów, w których wszystkie działania mają ten sam koszt, jest to takie samo, jak zachłanne wyszukiwanie „najlepiej najpierw”, ale gdy działania mają różne koszty, zwykle prowadzi wyszukiwanie do szybkiego znalezienia rozwiązania, nawet jeśli może to mieć wysoki koszt.

Przydatnym sposobem wizualizacji wyszukiwania jest narysowanie konturów w przestrzeni stanów, podobnie jak kontury na mapie topograficznej. Rysunek 3.20 pokazuje przykład. Wewnątrz konturu oznaczonego 400 wszystkie węzły mają f(n) =  g(n) + h(n) ≤ 400 i tak dalej. Następnie, ponieważ A* rozszerza węzeł graniczny o najniższym koszcie, możemy zobaczyć, że wyszukiwanie A* rozchodzi się od węzła początkowego, dodając węzły w koncentrycznych pasmach o rosnącym koszcie.

W przypadku wyszukiwania o jednolitym koszcie również mamy kontury, ale z opcją g-cost, nie g + h. Warstwice z wyszukiwaniem o jednolitym koszcie będą „kołowe” wokół stanu początkowego, rozłożone równomiernie we wszystkich kierunkach bez preferencji w kierunku celu. Przy wyszukiwaniu A* przy użyciu dobrej heurystyki, pasma g + h rozciągną się w kierunku stanu docelowego (jak na rysunku 3.20) i staną się węższe wokół optymalnej ścieżki. Powinno być jasne, że wraz z wydłużaniem ścieżki koszty są monotoniczne: koszt ścieżki zawsze wzrasta wraz z jej postępem, ponieważ koszty działania są zawsze dodatnie. Dlatego otrzymujesz koncentryczne linie konturowe, które się nie przecinają, a jeśli zdecydujesz się narysować je wystarczająco precyzyjnie, możesz umieścić linię między dowolnymi dwoma węzłami na dowolnej ścieżce.

Nie jest jednak oczywiste, czy koszty  f= g + h będą monotonnie rosły. Gdy rozszerzasz ścieżkę od n do n‘, koszt od g(n) + h(n) do g(n) + c(n,a,n’) + h(n’) Anulowanie terminu g(n), widzimy, że koszt ścieżki będzie monotonicznie wzrastał wtedy i tylko wtedy, gdy h(n) ≤ c(n,a,n’) + h(n’)   innymi słowy wtedy i tylko wtedy, gdy heurystyka jest spójna. Zauważ jednak, że ścieżka może wnosić kilka węzłów z rzędu z tym samym wynikiem g(n) + h(n); dzieje się tak, gdy spadek jest dokładnie równy kosztowi podjętej akcji (na przykład w przypadku problemu z siatką, gdy n znajduje się w tym samym wierszu co cel i robisz krok w kierunku celu, jest zwiększany o 1 i zmniejszany o 1). Jeżeli C*jest to koszt optymalnej ścieżki rozwiązania, to możemy powiedzieć, że:

* A* rozwija wszystkie węzły, do których można dotrzeć ze stanu początkowego na ścieżce, gdzie każdy węzeł na ścieżce posiada f(n) < C^* Mówimy, że są to z pewnością węzły rozwinięte

* A* może następnie rozwinąć niektóre węzły bezpośrednio na „obrysie celu” (gdzie f(n) = C*) przed wybraniem węzła celu.

* A* nie rozwija żadnych węzłów z f(n) > C*

Mówimy, że A* ze spójną heurystyką jest optymalnie wydajny w tym sensie, że każdy algorytm, który rozszerza ścieżki wyszukiwania ze stanu początkowego i używa tej samej informacji heurystycznej, musi rozwinąć wszystkie węzły, które z pewnością są rozwinięte przez A* (ponieważ którykolwiek z mogły być częścią optymalnego rozwiązania). Wśród węzłów f(n) = C* jednym algorytmem może mieć szczęście i wybrać ten optymalny, ponieważ inny algorytm ma pecha; nie bierzemy pod uwagę tej różnicy w definiowaniu optymalnej wydajności.

A* jest wydajny, ponieważ usuwa węzły drzewa wyszukiwania, które nie są konieczne do znalezienia optymalnego rozwiązania. Wcześniej widzieliśmy, że Timisoara ma f = 447 , a Zerind ma f = 449.Nawet jeśli są dziećmi pierwiastka i byłyby jednymi z pierwszych węzłów rozwijanych przez wyszukiwanie jednostajne lub wszerz, nigdy nie są rozwijane przez wyszukiwanie A*, ponieważ rozwiązanie z f = 418 jest znalezione jako pierwsze. Koncepcja przycinania – ograniczanie możliwości od rozważania bez konieczności ich badania – jest ważna dla wielu obszarów SI.

To, że wyszukiwanie A* jest kompletne, optymalne kosztowo i optymalnie wydajne wśród wszystkich takich algorytmów, jest raczej satysfakcjonujące. Niestety nie oznacza to, że A* jest odpowiedzią na wszystkie nasze potrzeby poszukiwawcze. Połów polega na tym, że w przypadku wielu problemów liczba rozwiniętych węzłów może być wykładnicza w długości rozwiązania. Rozważmy na przykład wersję świata próżni z superpotężną próżnią, która może wyczyścić dowolny kwadrat za cenę 1 jednostki, nawet bez konieczności odwiedzania placu; w tym scenariuszu kwadraty można czyścić w dowolnej kolejności. W przypadku N początkowo brudnych kwadratów istnieją  2^N stany, w których jakiś podzbiór został oczyszczony; wszystkie te stany znajdują się na optymalnej ścieżce rozwiązania, a więc spełniają f(n) < C^*, więc wszystkie byłyby odwiedzane przez A*.