Wyjaśniliśmy różnicę między środowiskami dyskretnymi i ciągłymi, wskazując, że większość środowisk świata rzeczywistego jest ciągła. Ciągła przestrzeń działania ma nieskończony czynnik rozgałęzienia, a zatem nie może być obsłużona przez większość algorytmów, które omówiliśmy do tej pory (z wyjątkiem wspinaczki pod górę pierwszego wyboru i symulowanego wyżarzania). Ta sekcja zawiera bardzo krótkie wprowadzenie do niektórych lokalnych technik wyszukiwania spacji ciągłych. Literatura na ten temat jest obszerna; wiele podstawowych technik powstało w XVII wieku, po opracowaniu rachunku różniczkowego przez Newtona i Leibniza. Zastosowania tych technik znajdujemy w kilku miejscach tej książki, w tym w rozdziałach dotyczących uczenia się, wizji i robotyki. Zaczynamy od przykładu. Załóżmy, że chcemy umieścić trzy nowe lotniska w dowolnym miejscu w Rumunii, tak aby zminimalizować sumę kwadratów odległości w linii prostej od każdego miasta na mapie do najbliższego lotniska. Przestrzeń państwowa jest następnie definiowana przez współrzędne trzech lotnisk: (x1,y1) , (x2,y2) i (x3,y3). To jest sześciowymiarowa przestrzeń; mówimy również, że stany są definiowane przez sześć zmiennych. Ogólnie, stany są definiowane przez dwuwymiarowy wektor zmiennych, . Poruszanie się w tej przestrzeni odpowiada przesuwaniu jednego lub więcej lotnisk na mapie. Funkcja celu f(x) = f(x1,y1,x2,y2,x3,y3) jest stosunkowo łatwa do obliczenia dla dowolnego konkretnego stanu po obliczeniu najbliższych miast. Niech Ci będzie zbiorem miast, których najbliższym lotniskiem (w stanie x) jest lotnisko . Potem będzie
Równanie to jest poprawne nie tylko dla stanu, ale także dla stanów x w lokalnym sąsiedztwie x. Jednak globalnie nie jest to poprawne; jeśli oddalimy się zbyt daleko (zmieniając położenie jednego lub więcej lotnisk o dużą wartość), to zestaw najbliższych miast tego lotniska zmienia się i musimy ponownie obliczyć Ci . Jednym ze sposobów radzenia sobie z ciągłą przestrzenią stanów jest jej dyskretyzacja. Na przykład, zamiast pozwalać, aby lokalizacje (x1,y1) były dowolnymi punktami w ciągłej dwuwymiarowej przestrzeni, moglibyśmy ograniczyć je do stałych punktów na prostokątnej siatce z odstępami wielkości (delta). Wtedy zamiast nieskończonej liczby następców, każdy stan w przestrzeni miałby tylko 12 następców, co odpowiada zwiększeniu jednej z 6 zmiennych o +/-δ. Następnie możemy zastosować dowolny z naszych lokalnych algorytmów wyszukiwania do tej dyskretnej przestrzeni. Alternatywnie moglibyśmy uczynić czynnik rozgałęzienia skończony przez losowe próbkowanie stanów następczych, poruszając się w losowym kierunku o niewielką wartość, . Metody mierzące postęp poprzez zmianę wartości funkcji celu pomiędzy dwoma pobliskimi punktami nazywane są empirycznymi metodami gradientowymi. Empiryczne poszukiwanie gradientu jest tym samym, co wspinaczka po najbardziej stromych zboczach w dyskretnej wersji przestrzeni stanów. Zmniejszenie wartości w czasie może dać dokładniejsze rozwiązanie, ale niekoniecznie zbiega się do globalnego optimum w limicie.
Często mamy funkcję celu wyrażoną w postaci matematycznej, tak że możemy użyć rachunku różniczkowego do rozwiązania problemu analitycznie, a nie empirycznie. Wiele metod próbuje wykorzystać gradient krajobrazu, aby znaleźć maksimum. Gradient funkcji celu jest wektorem f, który podaje wielkość i kierunek najbardziej stromego zbocza. Na nasz problem mamy
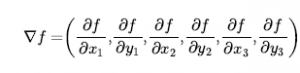
W niektórych przypadkach możemy znaleźć maksimum, rozwiązując równanie 
. (Można to zrobić, na przykład, gdybyśmy umieścili tylko jedno lotnisko; rozwiązaniem jest średnia arytmetyczna wszystkich współrzędnych wszystkich miast.) Jednak w wielu przypadkach tego równania nie da się rozwiązać w postaci zamkniętej. Na przykład w przypadku trzech lotnisk wyrażenie określające gradient zależy od tego, które miasta znajdują się najbliżej każdego lotniska w obecnym stanie. Oznacza to, że możemy obliczyć gradient lokalnie (ale nie globalnie); na przykład,
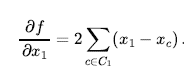
Mając lokalnie poprawne wyrażenie dla gradientu, możemy wykonać wspinaczkę pod górę o najbardziej stromym wzniesieniu, aktualizując aktualny stan zgodnie ze wzorem
gdzie α (alfa) jest małą stałą często nazywaną wielkością kroku. Istnieje ogromna różnorodność metod dostosowywania α . Podstawowym problemem jest to, że jeśli α jest za mały, to wymaga zbyt wielu kroków; jeśli α jest zbyt duży, wyszukiwanie może przekroczyć maksimum. Technika przeszukiwania linii próbuje przezwyciężyć ten dylemat, rozszerzając bieżący kierunek gradientu — zwykle przez wielokrotne podwajanie α – aż do ponownego spadku. Punkt, w którym to nastąpi, staje się nowym stanem obecnym. Istnieje kilka szkół myślenia o tym, jak należy obrać nowy kierunek w tym momencie.
W przypadku wielu problemów najskuteczniejszym algorytmem jest czcigodna metoda Newtona-Raphsona. Jest to ogólna technika znajdowania pierwiastków funkcji, czyli rozwiązywania równań postaci g(x) = 0 . Działa poprzez obliczenie nowego oszacowania pierwiastka x zgodnie ze wzorem Newtona
Aby znaleźć maksimum lub minimum f, musimy znaleźć x takie, że gradient jest wektorem zerowym (tj. 
). Zatem g(x) we wzorze Newtona staje się , a równanie uaktualniające można zapisać w postaci macierzowo-wektorowej jako
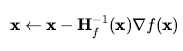
gdzie Hf(x) jest hesowską macierzą drugich pochodnych, której elementy Hij są podane przez 
. W naszym przykładzie z lotniskiem widzimy z równania , że Hf(x) jest szczególnie proste: elementy poza przekątną wynoszą zero, a elementy przekątne lotniska to tylko dwa razy więcej miast w C1 . Chwilowe obliczenia pokazują, że jeden krok aktualizacji przenosi lotnisko bezpośrednio do środka ciężkości Ci, który jest minimum lokalnego wyrażenia dla f z równania (4.1) . Jednak w przypadku problemów wysokowymiarowych obliczenie n2 wpisów hessu i odwrócenie go może być kosztowne, dlatego opracowano wiele przybliżonych wersji metody Newtona-Raphsona. Lokalne metody wyszukiwania cierpią z powodu lokalnych maksimów, grzbietów i płaskowyżów w przestrzeniach stanów ciągłych tak samo jak w przestrzeniach dyskretnych. Często pomocne są losowe restarty i symulowane wyżarzanie. Wysokowymiarowe przestrzenie ciągłe to jednak duże miejsca, w których bardzo łatwo się zgubić. Ostatnim tematem jest ograniczona optymalizacja. Problem optymalizacji jest ograniczony, jeśli rozwiązania muszą spełniać pewne twarde ograniczenia dotyczące wartości zmiennych. Na przykład, w naszym problemie z lokalizacją lotnisk, możemy ograniczyć lokalizację terenów na terenie Rumunii i na suchym lądzie (a nie w środku jezior). Trudność problemów optymalizacji z ograniczeniami zależy od charakteru ograniczeń i funkcji celu. Najbardziej znaną kategorią jest problem programowania liniowego, w którym ograniczenia muszą być nierównościami liniowymi tworzącymi zbiór wypukły, a funkcja celu jest również liniowa. Złożoność czasowa programowania liniowego jest wielomianowa w liczbie zmiennych. Programowanie liniowe jest prawdopodobnie najszerzej badaną i powszechnie przydatną metodą optymalizacji. Jest to szczególny przypadek bardziej ogólnego problemu optymalizacji wypukłej, który pozwala, aby obszarem ograniczeń był dowolny obszar wypukły, a celem była dowolna funkcja, która jest wypukła w obszarze ograniczeń. W pewnych warunkach wypukłe problemy optymalizacji są również rozwiązywalne wielomianowo i mogą być wykonalne w praktyce z tysiącami zmiennych. Kilka ważnych problemów związanych z uczeniem maszynowym i teorią sterowania można sformułować jako wypukłe problemy optymalizacji.