Algorytmy ewolucyjne można postrzegać jako warianty stochastycznego wyszukiwania wiązek, które są wyraźnie motywowane metaforą doboru naturalnego w biologii: istnieje populacja osobników (stanów), w której najsilniejsze (o najwyższej wartości) osobniki produkują potomstwo (stany następcze), które zaludnienie następnego pokolenia, proces zwany rekombinacją. Istnieje nieskończona liczba form algorytmów ewolucyjnych, różniących się w następujący sposób:
*Wielkość populacji.
*Reprezentacja każdej osoby. W algorytmach genetycznych każda osoba jest ciągiem nad skończonym alfabetem (często ciągiem logicznym), tak jak DNA jest ciągiem nad alfabetem ACGT. W strategiach ewolucyjnych jednostka jest sekwencją liczb rzeczywistych, a w programowaniu genetycznym jednostka jest programem komputerowym.
*Liczba mieszańców, która jest liczbą rodziców, którzy tworzą potomstwo. Najczęstszym przypadkiem jest ρ = 2: dwoje rodziców łączy swoje „geny” (części swojej reprezentacji), aby utworzyć potomstwo. Gdy ρ = 1 mamy stochastyczne przeszukiwanie wiązki (co może być postrzegane jako rozmnażanie bezpłciowe). Możliwe jest uzyskanie ρ > 2, co zdarza się rzadko w przyrodzie, ale jest wystarczająco łatwe do symulacji na komputerach.
*Proces selekcji osobników, które staną się rodzicami następnego pokolenia: jedną z możliwości jest wybór spośród wszystkich osobników z prawdopodobieństwem proporcjonalnym do ich wyniku sprawności. Inną możliwością jest losowe wybranie n osobników (n > ρ ), a następnie wybranie ρ najbardziej odpowiednich jako rodziców.
* Procedura rekombinacji. Jednym z powszechnych podejść (zakładając ρ = 2) jest losowy wybór punktu przecięcia w celu podzielenia każdego z ciągów rodzica i ponowne połączenie części w celu utworzenia dwojga dzieci, jednego z pierwszą częścią rodzica 1 i drugą częścią rodzica 2; druga z drugą częścią rodzica 1 i pierwszą częścią rodzica 2.
* Szybkość mutacji, która określa, jak często potomstwo ma losowe mutacje w swojej reprezentacji. Po wygenerowaniu potomstwa każdy bit w jego składzie jest odwracany z prawdopodobieństwem równym szybkości mutacji.
* Makijaż następnej generacji. Może to być tylko nowo uformowane potomstwo lub może obejmować kilku najlepszych rodziców z poprzedniego pokolenia (praktyka nazywana elitarnością, która gwarantuje, że ogólna sprawność nigdy nie spadnie z czasem). Praktyka uboju, w której odnotowuje się wszystkie osobniki poniżej określonego progu, prowadzi do przyspieszenia
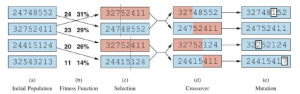
Algorytm genetyczny, zilustrowany dla ciągów cyfr reprezentujących stany 8-królowych. Populacja początkowa w (a) jest uszeregowana według funkcji przystosowania w (b), w wyniku czego powstają pary do krycia w (c). Wytwarzają potomstwo w (d), które podlega mutacji w (e).
Rysunek (a) pokazuje populację czterech 8-cyfrowych ciągów, z których każdy reprezentuje stan układanki z ośmioma hetmanami: -ta cyfra reprezentuje numer rzędu hetmana w kolumnie . W (b) każdy stan jest oceniany przez funkcję sprawności. Wyższe wartości sprawności są lepsze, więc dla 8-problemu hetmanów używamy do rozwiązania liczby nieatakujących par hetmanów, która ma wartość 8 x 7/2 = 28. Wartości czterech stanów w (b) to 24, 23, 20 i 11. Oceny sprawności są następnie znormalizowane do prawdopodobieństw, a otrzymane wartości są pokazane obok wartości sprawności w (b).
Algorytm genetyczny, zilustrowany dla ciągów cyfr reprezentujących stany 8-królowych. Populacja początkowa w (a) jest uszeregowana według funkcji przystosowania w (b), w wyniku czego powstają pary do krycia w (c). Wytwarzają potomstwo w (d), które podlega mutacji w (e). W (c) wybiera się dwie pary rodziców zgodnie z prawdopodobieństwami z (b). Zauważ, że jedna osoba została wybrana dwukrotnie, a druga wcale. Dla każdej wybranej pary losowo wybierany jest punkt przecięcia (linia przerywana). W (d) krzyżujemy struny rodzicielskie w punktach przecięcia, dając nowe potomstwo. Na przykład pierwsze dziecko z pierwszej pary otrzymuje pierwsze trzy cyfry (327) od pierwszego rodzica, a pozostałe cyfry (48552) od drugiego rodzica. 8 stanów królowych biorących udział w tym etapie rekombinacji pokazano na rycinie

8 stanów matek odpowiadających dwóm pierwszym rodzicom z ryciny (c) i pierwszemu potomstwu z ryciny (d). Zielone kolumny są tracone w kroku krzyżowania, a czerwone kolumny pozostają. (Aby zinterpretować liczby na rysunku: wiersz 1 to wiersz dolny, a wiersz 8 to wiersz górny).
Wreszcie w (e) każda lokalizacja w każdym ciągu podlega losowej mutacji z małym niezależnym prawdopodobieństwem. Jedna cyfra została zmutowana u pierwszego, trzeciego i czwartego potomstwa. W zagadnieniu 8 hetmanów odpowiada to losowemu wybraniu hetmana i przesunięciu go na losowe pole w jego kolumnie. Często jest tak, że populacja jest zróżnicowana na wczesnym etapie procesu, więc krzyżowanie często wykonuje duże kroki w przestrzeni stanów na początku procesu wyszukiwania (jak w symulowanym wyżarzaniu). Po wielu pokoleniach selekcji w kierunku wyższej sprawności populacja staje się mniej zróżnicowana i typowe są mniejsze kroki. Rysunek opisuje algorytm, który implementuje wszystkie te kroki.

Algorytmy genetyczne są podobne do stochastycznego wyszukiwania wiązki, ale z dodatkiem operacji krzyżowania. Jest to korzystne, jeśli istnieją bloki, które wykonują przydatne funkcje. Na przykład może się zdarzyć, że umieszczenie pierwszych trzech hetmanów w pozycjach 2, 4 i 6 (gdzie nie atakują się nawzajem) stanowi przydatny bloczek, który można połączyć z innymi przydatnymi bloczkami, które pojawiają się u innych osobników, aby skonstruować rozwiązanie . Można wykazać matematycznie, że jeśli bloki nie służą celowi – na przykład jeśli pozycje kodu genetycznego są losowo permutowane – to krzyżowanie nie daje żadnej korzyści. Teoria algorytmów genetycznych wyjaśnia, jak to działa, wykorzystując ideę schematu, który jest podciągiem, w którym niektóre pozycje można pozostawić nieokreślone. Na przykład schemat 246***** opisuje wszystkie stany 8-matek, w których pierwsze trzy królowe znajdują się odpowiednio na pozycjach 2, 4 i 6. Ciągi pasujące do schematu (takie jak 24613578) są nazywane instancjami schematu. Można wykazać, że jeśli średnia dopasowanie instancji schematu jest powyżej średniej, to liczba instancji schematu będzie z czasem rosła.