Istnieją usługi online, które udostępniają mapy z dziesiątkami milionów wierzchołków i znajdują optymalne pod względem kosztów wskazówki dojazdu w milisekundach. Jak mogą to zrobić, skoro najlepsze algorytmy wyszukiwania, które do tej pory rozważaliśmy, są około milion razy wolniejsze? Istnieje wiele sztuczek, ale najważniejszą z nich jest wstępne obliczenie niektórych optymalnych kosztów ścieżki. Chociaż wstępne obliczenia mogą być czasochłonne, należy je wykonać tylko raz, a następnie można je amortyzować przez miliardy żądań wyszukiwania użytkowników.
Moglibyśmy wygenerować idealną heurystykę, wstępnie obliczając i przechowując koszt optymalnej ścieżki między każdą parą wierzchołków. Zajęłoby to przestrzeń O(|V|2) i czas O(|E|3) – praktyczne dla grafów z 10 tysiącami wierzchołków, ale nie z 10 milionami. Lepszym podejściem jest wybranie kilku (być może 10 lub 20) punktów orientacyjnych z wierzchołków. Następnie dla każdego punktu orientacyjnego L i dla każdego innego wierzchołka na wykresie obliczamy i przechowujemy C*(v,L) dokładny koszt optymalnej ścieżki od v do L. (Potrzebujemy również na C*(L,v); graf nieskierowany to to samo, co C*(v,L) na grafie skierowanym—np. z ulicami jednokierunkowymi—musimy to obliczyć osobno.) Mając zapisane tabele C*, możemy łatwo stworzyć wydajną ( chociaż niedopuszczalne) heurystyka: minimalny koszt dotarcia z bieżącego węzła do punktu orientacyjnego, a następnie do celu, ponad wszystkimi punktami orientacyjnymi:
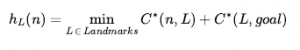
Jeśli optymalna ścieżka przechodzi przez punkt orientacyjny, ta heurystyka będzie dokładna; jeśli nie, to jest niedopuszczalne – zawyża koszt do celu. W wyszukiwaniu A*, jeśli masz dokładną heurystykę, to po dotarciu do węzła, który znajduje się na optymalnej ścieżce, każdy węzeł, który rozwiniesz od tego momentu, będzie na optymalnej ścieżce. Pomyśl o liniach konturowych jako podążających wzdłuż tej optymalnej ścieżki. Wyszukiwanie będzie przebiegać wzdłuż optymalnej ścieżki, w każdej iteracji dodając akcję z kosztem, aby uzyskać wynik, którego wartość będzie mniejsza, co oznacza, że całkowity wynik f = g + h pozostanie stały na C* na całej ścieżce . Niektóre algorytmy wyszukiwania tras oszczędzają jeszcze więcej czasu, dodając skróty – sztuczne krawędzie na wykresie, które definiują optymalną ścieżkę wielu działań. Na przykład, gdyby istniały wstępnie zdefiniowane skróty między wszystkimi 100 największymi miastami w Stanach Zjednoczonych, a my próbowaliśmy nawigować z kampusu Berkeley w Kalifornii do NYU w Nowym Jorku, moglibyśmy skorzystać ze skrótu między Sacramento a Manhattanem i objąć 90% ścieżka w jednej akcji.
hL(n) jest skuteczny, ale niedopuszczalny. Ale z większą ostrożnością możemy wymyślić heurystykę, która jest zarówno skuteczna, jak i dopuszczalna:
![]()
Nazywa się to heurystyką różniczkową (z powodu odejmowania). Pomyśl o tym z punktem orientacyjnym, który znajduje się gdzieś poza celem. Jeśli cel znajduje się na optymalnej ścieżce od n do punktu orientacyjnego, oznacza to: „rozważ całą ścieżkę od n do L, a następnie odejmij ostatnią część tej ścieżki, od celu do L, dając nam dokładny koszt ścieżka od n do celu.” Do tego stopnia, że cel jest nieco poza optymalną ścieżką do punktu orientacyjnego, heurystyka będzie niedokładna, ale nadal dopuszczalna. Punkty orientacyjne, które nie znajdują się poza celem, nie będą przydatne; punkt orientacyjny, który znajduje się dokładnie w połowie drogi między n a celem, da hDH = 0, co nie jest pomocne. Istnieje kilka sposobów na wybranie punktów orientacyjnych. Losowe wybieranie punktów jest szybkie, ale lepsze wyniki uzyskujemy, jeśli zadbamy o rozmieszczenie punktów orientacyjnych, aby nie znajdowały się zbyt blisko siebie. Chciwym podejściem jest losowe wybranie pierwszego punktu orientacyjnego, a następnie znalezienie punktu, który jest najbardziej od niego oddalony, dodanie go do zestawu punktów orientacyjnych i kontynuowanie w każdej iteracji + dodanie punktu, który maksymalizuje odległość do najbliższy punkt orientacyjny. Jeśli masz dzienniki wcześniejszych żądań wyszukiwania przez użytkowników, możesz wybrać punkty orientacyjne, które są często wymagane w wyszukiwaniach. W przypadku heurystyki różnicowej dobrze jest, jeśli punkty orientacyjne są rozmieszczone na obwodzie wykresu. Tak więc dobrą techniką jest znalezienie środka ciężkości wykresu, ułożenie klinów w kształcie koła wokół środka ciężkości, aw każdym klinie wybranie wierzchołka, który jest najdalej od środka. Punkty orientacyjne sprawdzają się szczególnie dobrze w problemach ze znajdowaniem tras ze względu na sposób rozmieszczenia dróg na świecie: duży ruch faktycznie chce podróżować między punktami orientacyjnymi, więc inżynierowie budowlani budują najszersze i najszybsze drogi wzdłuż tych tras; wyszukiwanie punktów orientacyjnych ułatwia odzyskanie tych tras.