Przyjrzymy się, jak dokładność heurystyki wpływa na wydajność wyszukiwania, a także rozważymy, jak można wymyślić heurystykę. Jako nasz główny przykład powrócimy do 8-zagadki. Jak wspomniano w Sekcji 3.2, celem łamigłówki jest przesuwanie płytek poziomo lub pionowo w pustą przestrzeń, aż konfiguracja będzie pasować do konfiguracji celu.
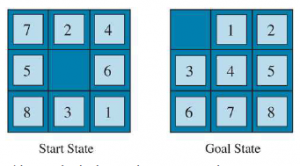
W 8 Puzzle jest 9!/2 = 181 400 osiągalnych stanów, więc wyszukiwanie może z łatwością zachować je wszystkie w pamięci. Ale dla 15-puzzli jest 16!/2 stanów – ponad 10 bilionów – więc aby przeszukać tę przestrzeń, będziemy potrzebować pomocy dobrej, dopuszczalnej funkcji heurystycznej. Istnieje długa historia takich heurystyk dla 15-puzzli; oto dwa powszechnie używane kandydaci:
* h1 = liczba zagubionych płytek (brak pustego miejsca). Na rysunku 3.25 wszystkie osiem płytek jest nie na miejscu, więc stan początkowy ma h1 = 8, h1 jest dopuszczalną heurystyką, ponieważ każda płytka, która jest nie na miejscu, będzie wymagała co najmniej jednego ruchu, aby umieścić ją we właściwym miejscu.
* h2 = suma odległości płytek od ich pozycji bramkowych. Ponieważ kafelki nie mogą się poruszać po przekątnych, odległość jest sumą odległości poziomych i pionowych – czasami nazywanej odległością między miastami lub Manhattanem. h2 jest również dopuszczalne, ponieważ każdy ruch może zrobić, to przesunąć jedną płytkę o jeden krok bliżej celu. Kafelki od 1 do 8 w stanie początkowym na rysunku 3.25 dają odległość Manhattanu
h2 = 3 + 1 + 2 + 2 + 2 + 3 + 3 + 2 = 18.
Zgodnie z oczekiwaniami żadne z nich nie zawyża rzeczywistego kosztu rozwiązania, który wynosi 26.
3.6.1 Wpływ dokładności heurystycznej na wydajność
Jednym ze sposobów scharakteryzowania jakości heurystyki jest efektywny współczynnik rozgałęzienia b*. Jeśli całkowita liczba węzłów wygenerowanych przez A* dla konkretnego problemu wynosi N, a głębokość rozwiązania wynosi d, to b* jest współczynnikiem rozgałęzienia, który musiałoby mieć jednolite drzewo o głębokości d, aby zawierało N+1 węzłów. Zatem,
N + 1 = 1 + b∗ + (b∗)2 +⋯+ (b∗)d.
Na przykład, jeśli A* znajdzie rozwiązanie na głębokości 5 przy użyciu 52 węzłów, to efektywny współczynnik rozgałęzienia wynosi 1,92. Efektywny współczynnik rozgałęzienia może się różnić w różnych instancjach problemów, ale zwykle dla określonej domeny (takiej jak 8-zagadek) jest dość stały we wszystkich nietrywialnych instancjach problemów. Dlatego eksperymentalne pomiary b* na małym zestawie problemów mogą stanowić dobry przewodnik po ogólnej użyteczności heurystyki. Dobrze zaprojektowana heurystyka miałaby wartość b* bliską 1, pozwalając na rozwiązanie dość dużych problemów przy rozsądnych kosztach obliczeniowych. Korf i Reid twierdzą, że lepszym sposobem scharakteryzowania efektu przycinania A* przy użyciu danej heurystyki jest zmniejszenie głębokości efektywnej o stałą wartość kh w porównaniu z głębokością rzeczywistą. Oznacza to, że całkowity koszt wyszukiwania wynosi O(bd-kh) w porównaniu z O(bd) w przypadku wyszukiwania bez informacji. Eksperymenty z kostką Rubika i problemami łamigłówkowymi pokazują, że ta formuła daje dokładne prognozy całkowitego kosztu wyszukiwania dla próbkowanych instancji problemów w szerokim zakresie długości rozwiązań – przynajmniej dla rozwiązań o długości większej niż kh.
Dla rysunku wygenerowaliśmy losowe problemy z ośmioma łamigłówkami i rozwiązaliśmy je za pomocą niedoinformowanego przeszukiwania wszerz oraz przeszukiwania A* przy użyciu zarówno h1 i h2 podających średnią liczbę wygenerowanych węzłów i odpowiadający jej efektywny współczynnik rozgałęzienia dla każdej strategii wyszukiwania i dla każdej długości rozwiązania. Wyniki sugerują, że h2 jest lepsze niż h1 i oba są lepsze niż brak heurystyki.
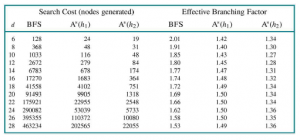
Porównanie kosztów wyszukiwania i efektywnych współczynników rozgałęzienia dla problemów z 8 łamigłówkami przy użyciu szerokości na pierwszym miejscu
szukaj, A* z
h1
(zagubione płytki) i A* z
h2
(Odległość Manhattanu). Dane są uśredniane z ponad 100 puzzli dla każdej długości rozwiązania
d
od 6 do 28.
Można by zapytać, czy h2 jest zawsze lepsze niż h1. Odpowiedź brzmi: „Zasadniczo tak”. Łatwo zauważyć z definicji obu heurystyk, że dla dowolnego węzła n ,h2(n) ≥ h1(n) Mówimy zatem, że h2 dominuje nad h1. Dominacja przekłada się bezpośrednio na efektywność: A* używający h2 nigdy nie rozwinie więcej węzłów niż A* używający h1 (poza przypadkowym zerwaniem więzi). Argument jest prosty. Przypomnij sobie obserwację, że każdy węzeł z f(n) < C* na pewno zostanie rozszerzony. To to samo, co powiedzenie, że każdy węzeł z h(n) < C* – g(n) jest na pewno rozwinięty, gdy jest niesprzeczny. Ale ponieważ h2 jest co najmniej tak duże jak h1 dla wszystkich węzłów, każdy węzeł, który z pewnością jest rozszerzany przez przeszukiwanie A* z h2 jest również z pewnością rozszerzany z h1 i może spowodować rozwinięcie innych węzłów. Dlatego generalnie lepiej jest użyć funkcji heurystycznej o wyższych wartościach, pod warunkiem, że jest ona spójna i czas obliczeń heurystyki nie jest zbyt długi.