W przypadku jednokierunkowego wyszukiwania typu „najlepszy-pierwszy” zauważyliśmy, że użycie f(n) = g(n) + h(n) jako funkcji oceny daje nam przeszukiwanie A*, które gwarantuje znalezienie rozwiązań o optymalnym koszcie (przy założeniu dopuszczalnego ), a jednocześnie jest optymalnie wydajne pod względem liczby rozwiniętych węzłów. W przypadku dwukierunkowego wyszukiwania typu „najlepszy-pierwszy” moglibyśmy również spróbować użyć f(n) = g(n) + h(n) , ale niestety nie ma gwarancji, że doprowadzi to do rozwiązania o optymalnych kosztach ani że będzie optymalnie wydajne, nawet przy dopuszczalnej heurystyce. Przy wyszukiwaniu dwukierunkowym okazuje się, że to nie pojedyncze węzły, ale raczej pary węzłów (po jednym z każdej granicy) można udowodnić, że są na pewno rozwinięte, więc każdy dowód wydajności będzie musiał uwzględniać pary węzłów. Zaczniemy od nowej notacji. Używamy fF(n) = gF(n) + hF(n) dla węzłów idących w przód (ze stanem początkowym jako root) oraz fB(n) = gB(n) + hB(n) dla węzłów w kierunku wstecznym (ze stanem docelowym jako root). Chociaż zarówno wyszukiwanie do przodu, jak i do tyłu rozwiązuje ten sam problem, mają różne funkcje oceny, ponieważ na przykład heurystyki różnią się w zależności od tego, czy dążysz do celu, czy do stanu początkowego. Założymy dopuszczalną heurystykę. Rozważ ścieżkę w przód od stanu początkowego do węzła m i ścieżkę powrotną od celu do węzła n. Możemy zdefiniować dolne ograniczenie kosztu rozwiązania, które podąża ścieżką od stanu początkowego do m następnie w jakiś sposób dociera do n , a następnie podąża ścieżką do celu jako
lb(m,n) = max(gF(m) + gB(n),fF(m),fB(n)
Innymi słowy, koszt takiej ścieżki musi być co najmniej tak duży, jak suma kosztów ścieżki obu części (ponieważ pozostałe połączenie między nimi musi mieć koszt nieujemny), a koszt również musi być co najmniej tyle, ile szacowany koszt każdej części (ponieważ szacunki heurystyczne są optymistyczne). Biorąc to pod uwagę, twierdzenie jest takie, że dla dowolnej pary węzłów (m,n) z lb(m,n) o koszcie mniejszym niż optymalny C*musimy rozszerzyć m albo n ponieważ ścieżka, która przechodzi przez oba z nich, jest potencjalnie optymalnym rozwiązaniem. Trudność polega na tym, że nie wiemy na pewno, który węzeł najlepiej rozwinąć, a zatem żaden algorytm wyszukiwania dwukierunkowego nie może zagwarantować, że będzie optymalnie wydajny – każdy algorytm może rozszerzyć do dwukrotności minimalnej liczby węzłów, jeśli zawsze wybierze złą składową pary, która ma się rozwinąć jako pierwsza. Niektóre algorytmy dwukierunkowego wyszukiwania heurystycznego wprost zarządzają kolejką par (m,n), ale pozostaniemy przy dwukierunkowym wyszukiwaniu „najlepszy-pierwszy”, które ma dwie kolejki priorytetów granicznych, i nadamy mu funkcję oceny, która naśladuje kryteria lb:
f2(n) = max(2g(n), g(n) + h(n)
Węzeł do rozwinięcia jako następny będzie tym, który minimalizuje tę wartość f2 ; węzeł może pochodzić z dowolnej granicy. Ta funkcja f2 gwarantuje, że nigdy nie rozszerzymy węzła (z którejkolwiek granicy) z g(n) > C*/2. Mówimy, że dwie połowy wyszukiwania „spotykają się w środku” w tym sensie, że kiedy dwie granice się stykają, żaden węzeł wewnątrz żadnej z granic nie ma ścieżki koszt większy niż granica C*/2. Rysunek przedstawia przykładowe wyszukiwanie dwukierunkowe.
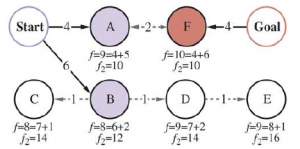
Wyszukiwanie dwukierunkowe utrzymuje dwie granice: po lewej węzły A i B są następcami Start; po prawej węzeł F jest odwrotnym następcą celu. Każdy węzeł jest oznaczony wartościami f = g + h i wartością f2 = max(2g, g + h) . (Wartości g są sumą kosztów działania, jak pokazano na każdej strzałce; wartości h są arbitralne i nie można ich wyprowadzić z niczego na rysunku). Optymalne rozwiązanie, Start-A-Goal, ma koszt C* = 4 + 2 + 4 = 10, co oznacza, że spotkanie- algorytm dwukierunkowy in-the-middle nie powinien rozszerzać żadnego węzła za pomocą g > C*/2 =5 i rzeczywiście następnym węzłem do rozwinięcia będzie A lub F (każdy z g = 4 ), co prowadzi nas do optymalnego rozwiązania. Gdybyśmy najpierw rozszerzyli węzeł o najniższym koszcie, wtedy B i C byłyby następne, a D i E byłyby powiązane z A, ale wszystkie mają g > C*/2 i dlatego nigdy nie są rozwijane, gdy f2 jest funkcja oceny.
Opisaliśmy podejście, w którym heurystyka hF szacuje odległość do celu (lub, gdy problem ma wiele stanów celu, odległość do najbliższego celu), a hB szacuje odległość do początku. Nazywa się to wyszukiwaniem od frontu do końca. Alternatywa, zwana przeszukiwaniem front-to-front, polega na próbie oszacowania odległości do drugiej granicy. Oczywiście, jeśli granica ma miliony węzłów, nieefektywne byłoby zastosowanie funkcji heurystycznej do każdego z nich i przyjęcie minimum. Ale może działać próbkowanie kilku węzłów z granicy. W pewnych specyficznych dziedzinach problemowych możliwe jest podsumowanie granicy — na przykład w przypadku przeszukiwania siatki możemy przyrostowo obliczyć ramkę graniczną i użyć jako heurystyki odległość do ramki granicznej. Wyszukiwanie dwukierunkowe jest czasami bardziej wydajne niż wyszukiwanie jednokierunkowe, czasami nie. Ogólnie rzecz biorąc, jeśli mamy bardzo dobrą heurystykę, to wyszukiwanie A* tworzy kontury wyszukiwania, które są skoncentrowane na celu, a dodanie wyszukiwania dwukierunkowego niewiele pomaga. Przy przeciętnym heurystycznym wyszukiwaniu dwukierunkowym, które spotyka się w środku, ma tendencję do rozszerzania mniejszej liczby węzłów i jest preferowane. W najgorszym przypadku słabej heurystyki wyszukiwanie nie jest już skoncentrowane na celu, a wyszukiwanie dwukierunkowe ma taką samą asymptotyczną złożoność jak A*. Wyszukiwanie dwukierunkowe z funkcją oceny f2 i dopuszczalną heurystyką jest kompletne i optymalne.