Wyszukiwanie* ma wiele dobrych cech, ale rozszerza wiele węzłów. Możemy zbadać mniej węzłów (zabierając mniej czasu i przestrzeni), jeśli jesteśmy gotowi zaakceptować rozwiązania, które są nieoptymalne, ale są „wystarczająco dobre” – co nazywamy satysfakcjonującymi rozwiązaniami. Jeśli pozwolimy wyszukiwaniu A* na użycie niedopuszczalnej heurystyki — takiej, która może być przeszacowana — ryzykujemy pominięcie optymalnego rozwiązania, ale heurystyka może być potencjalnie bardziej dokładna, zmniejszając w ten sposób liczbę rozwiniętych węzłów. Na przykład inżynierowie drogowi znają pojęcie wskaźnika objazdu, który jest mnożnikiem stosowanym do odległości w linii prostej w celu uwzględnienia typowej krzywizny dróg. Wskaźnik objazdu wynoszący 1,3 oznacza, że jeśli dwa miasta są oddalone od siebie o 10 mil w linii prostej, dobre oszacowanie najlepszej ścieżki między nimi wynosi 13 mil. Dla większości miejscowości wskaźnik objazdu waha się od 1,2 do 1,6. Możemy zastosować tę ideę do dowolnego problemu, nie tylko dotyczącego dróg, za pomocą podejścia zwanego przeszukiwaniem ważonym A*, w którym ważymy wartość heurystyczną bardziej, dając nam funkcję oceny f(n) = g(n) +W x h( n) dla niektórych W > 1. Rysunek pokazuje problem wyszukiwania w świecie siatki. W (a) wyszukiwanie A* znajduje optymalne rozwiązanie, ale aby je znaleźć, musi zbadać dużą część przestrzeni stanów. W (b) ważone wyszukiwanie A* znajduje rozwiązanie, które jest nieco droższe, ale czas wyszukiwania jest znacznie szybszy. Widzimy, że ważone wyszukiwanie skupia kontur osiągniętych stanów w kierunku celu. Oznacza to, że eksplorowanych jest mniej stanów, ale jeśli optymalna ścieżka kiedykolwiek wyjdzie poza kontur ważonego wyszukiwania (jak to ma miejsce w tym przypadku), to optymalna ścieżka nie zostanie znaleziona. Ogólnie rzecz biorąc, jeśli optymalne rozwiązanie kosztuje C* ważone wyszukiwanie A*, znajdzie rozwiązanie, które kosztuje gdzieś pomiędzy C* a W x C*, ale w praktyce zwykle otrzymujemy wyniki znacznie bliższe C* niż W x C*.
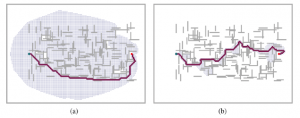
Dwa wyszukiwania na tej samej siatce: (a) wyszukiwanie A* i (b) wyszukiwanie ważone A* z wagą W = 2. Szare paski to przeszkody, fioletowa linia to ścieżka od zielonego startu do czerwonego celu, oraz małe kropki to stany osiągnięte podczas każdego wyszukiwania. W przypadku tego konkretnego problemu ważone A* bada 7 razy mniej stanów i znajduje ścieżkę, która jest o 5% droższa. Rozważaliśmy wyszukiwania, które oceniają stany przez łączenie i na różne sposoby; ważone A* można postrzegać jako uogólnienie pozostałych:
Wyszukiwanie A*: g(n) + h(n) (W = 1)
Wyszukiwanie według jednolitych kosztów: g(n) (W = 0)
Chciwe wyszukiwanie najpierw: h(n) (W = ∞)
Wyszukiwanie ważone A*: g(n) +W x h(n) (1 < W < ∞)
Możesz nazwać ważone A* „nieco zachłanne wyszukiwanie”: podobnie jak zachłanne wyszukiwanie „najlepiej-najpierw”, skupia ono wyszukiwanie na celu; z drugiej strony nie zignoruje całkowicie kosztu ścieżki i zawiesi ścieżkę, która robi niewielkie postępy wielkim kosztem. Istnieje wiele nieoptymalnych algorytmów wyszukiwania, które można scharakteryzować za pomocą kryteriów określających, co jest „wystarczająco dobre”. W ograniczonym wyszukiwaniu suboptymalnym szukamy rozwiązania, które gwarantuje, że mieści się w stałym współczynniku W kosztu optymalnego. Ważona A* zapewnia tę gwarancję. W wyszukiwaniu z kosztem ograniczonym szukamy rozwiązania, którego koszt jest mniejszy niż pewna stała C. A w wyszukiwaniu z kosztem nieograniczonym akceptujemy rozwiązanie o dowolnym koszcie, o ile możemy je szybko znaleźć. Przykładem algorytmu wyszukiwania o nieograniczonych kosztach jest szybkie wyszukiwanie, które jest wersją zachłannego wyszukiwania „najlepiej najpierw”, które wykorzystuje jako heurystykę szacowaną liczbę działań wymaganych do osiągnięcia celu, niezależnie od kosztu tych działań. Tak więc w przypadku problemów, w których wszystkie działania mają ten sam koszt, jest to takie samo, jak zachłanne wyszukiwanie „najlepiej najpierw”, ale gdy działania mają różne koszty, zwykle prowadzi wyszukiwanie do szybkiego znalezienia rozwiązania, nawet jeśli może to mieć wysoki koszt.