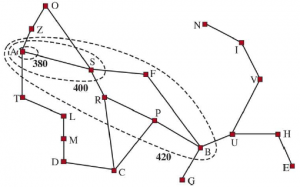
Przydatnym sposobem wizualizacji wyszukiwania jest narysowanie konturów w przestrzeni stanów, podobnie jak kontury na mapie topograficznej. Rysunek 3.20 pokazuje przykład. Wewnątrz konturu oznaczonego 400 wszystkie węzły mają f(n) = g(n) + h(n) ≤ 400 i tak dalej. Następnie, ponieważ A* rozszerza węzeł graniczny o najniższym koszcie, możemy zobaczyć, że wyszukiwanie A* rozchodzi się od węzła początkowego, dodając węzły w koncentrycznych pasmach o rosnącym koszcie.
W przypadku wyszukiwania o jednolitym koszcie również mamy kontury, ale z opcją g-cost, nie g + h. Warstwice z wyszukiwaniem o jednolitym koszcie będą „kołowe” wokół stanu początkowego, rozłożone równomiernie we wszystkich kierunkach bez preferencji w kierunku celu. Przy wyszukiwaniu A* przy użyciu dobrej heurystyki, pasma g + h rozciągną się w kierunku stanu docelowego (jak na rysunku 3.20) i staną się węższe wokół optymalnej ścieżki. Powinno być jasne, że wraz z wydłużaniem ścieżki koszty są monotoniczne: koszt ścieżki zawsze wzrasta wraz z jej postępem, ponieważ koszty działania są zawsze dodatnie. Dlatego otrzymujesz koncentryczne linie konturowe, które się nie przecinają, a jeśli zdecydujesz się narysować je wystarczająco precyzyjnie, możesz umieścić linię między dowolnymi dwoma węzłami na dowolnej ścieżce.
Nie jest jednak oczywiste, czy koszty f= g + h będą monotonnie rosły. Gdy rozszerzasz ścieżkę od n do n‘, koszt od g(n) + h(n) do g(n) + c(n,a,n’) + h(n’) Anulowanie terminu g(n), widzimy, że koszt ścieżki będzie monotonicznie wzrastał wtedy i tylko wtedy, gdy h(n) ≤ c(n,a,n’) + h(n’) innymi słowy wtedy i tylko wtedy, gdy heurystyka jest spójna. Zauważ jednak, że ścieżka może wnosić kilka węzłów z rzędu z tym samym wynikiem g(n) + h(n); dzieje się tak, gdy spadek jest dokładnie równy kosztowi podjętej akcji (na przykład w przypadku problemu z siatką, gdy n znajduje się w tym samym wierszu co cel i robisz krok w kierunku celu, jest zwiększany o 1 i zmniejszany o 1). Jeżeli C*jest to koszt optymalnej ścieżki rozwiązania, to możemy powiedzieć, że:
* A* rozwija wszystkie węzły, do których można dotrzeć ze stanu początkowego na ścieżce, gdzie każdy węzeł na ścieżce posiada f(n) < C* Mówimy, że są to z pewnością węzły rozwinięte
* A* może następnie rozwinąć niektóre węzły bezpośrednio na „obrysie celu” (gdzie f(n) = C*) przed wybraniem węzła celu.
* A* nie rozwija żadnych węzłów z f(n) > C*
Mówimy, że A* ze spójną heurystyką jest optymalnie wydajny w tym sensie, że każdy algorytm, który rozszerza ścieżki wyszukiwania ze stanu początkowego i używa tej samej informacji heurystycznej, musi rozwinąć wszystkie węzły, które z pewnością są rozwinięte przez A* (ponieważ którykolwiek z mogły być częścią optymalnego rozwiązania). Wśród węzłów f(n) = C* jednym algorytmem może mieć szczęście i wybrać ten optymalny, ponieważ inny algorytm ma pecha; nie bierzemy pod uwagę tej różnicy w definiowaniu optymalnej wydajności.
A* jest wydajny, ponieważ usuwa węzły drzewa wyszukiwania, które nie są konieczne do znalezienia optymalnego rozwiązania. Wcześniej widzieliśmy, że Timisoara ma f = 447 , a Zerind ma f = 449.Nawet jeśli są dziećmi pierwiastka i byłyby jednymi z pierwszych węzłów rozwijanych przez wyszukiwanie jednostajne lub wszerz, nigdy nie są rozwijane przez wyszukiwanie A*, ponieważ rozwiązanie z f = 418 jest znalezione jako pierwsze. Koncepcja przycinania – ograniczanie możliwości od rozważania bez konieczności ich badania – jest ważna dla wielu obszarów SI.
To, że wyszukiwanie A* jest kompletne, optymalne kosztowo i optymalnie wydajne wśród wszystkich takich algorytmów, jest raczej satysfakcjonujące. Niestety nie oznacza to, że A* jest odpowiedzią na wszystkie nasze potrzeby poszukiwawcze. Połów polega na tym, że w przypadku wielu problemów liczba rozwiniętych węzłów może być wykładnicza w długości rozwiązania. Rozważmy na przykład wersję świata próżni z superpotężną próżnią, która może wyczyścić dowolny kwadrat za cenę 1 jednostki, nawet bez konieczności odwiedzania placu; w tym scenariuszu kwadraty można czyścić w dowolnej kolejności. W przypadku N początkowo brudnych kwadratów istnieją 2N stany, w których jakiś podzbiór został oczyszczony; wszystkie te stany znajdują się na optymalnej ścieżce rozwiązania, a więc spełniają f(n) < C*, więc wszystkie byłyby odwiedzane przez A*.