Chciwe przeszukiwanie „najlepsze-pierwsze” jest formą przeszukiwania „najlepsze-pierwsze”, które rozwija najpierw węzeł z najniższą wartością – węzeł, który wydaje się być najbliżej celu – na tej podstawie, że może to szybko doprowadzić do rozwiązania. Zatem funkcja oceny f(n) = g(n).
Zobaczmy, jak to działa w przypadku problemów ze znajdowaniem tras w Rumunii; używamy heurystyki odległości w linii prostej, którą nazwiemy hSLD. Jeśli celem jest Bukareszt, musimy znać odległości do Bukaresztu w linii prostej, które pokazano tu .

Na przykład hSLD(Arad) = 366. Zauważ, że wartości hSLD nie można obliczyć na podstawie problemu
sam opis (czyli funkcje AKCJE i WYNIK). Co więcej, potrzeba pewnej wiedzy o świecie, aby wiedzieć, że hSLD jest skorelowane z rzeczywistymi odległościami drogowymi i dlatego jest użyteczną heurystyką.
Rysunek przedstawia postęp zachłannego wyszukiwania „najpierw najlepszy” przy użyciu hSLD w celu znalezienia drogi z Aradu do Bukaresztu.
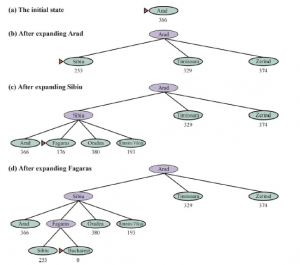
Pierwszym węzłem, który zostanie rozszerzony z Arad, będzie Sibiu, ponieważ heurystyka mówi, że jest bliżej Bukaresztu niż Zerind czy Timisoara. Następnym rozwiniętym węzłem będzie Fagaras, ponieważ jest teraz najbliżej według heurystyki. Fagaras z kolei generuje Bukareszt, który jest celem. W przypadku tego konkretnego problemu zachłanne wyszukiwanie „najpierw najlepszy” przy użyciu hSLD znajduje rozwiązanie bez rozszerzania węzła, który nie znajduje się na ścieżce rozwiązania. Znalezione rozwiązanie nie ma jednak optymalnych kosztów: trasa przez Sibiu i Fagaras do Bukaresztu jest o 32 mile dłuższa niż trasa przez Rimnicu Vilcea i Pitesti. Dlatego algorytm jest nazywany „chciwym” – w każdej iteracji stara się zbliżyć do celu jak tylko może, ale zachłanność może prowadzić do gorszych wyników niż bycie ostrożnym. Chciwe przeszukiwanie grafu „najlepszy-pierwszy” jest kompletne w skończonych przestrzeniach stanów, ale nie w nieskończonych. Najgorszy przypadek złożoności czasowej i przestrzennej to O(|V|). Jednak przy dobrej funkcji heurystycznej złożoność można znacznie zmniejszyć, przy pewnych problemach osiągających O(bm).