Aby uchronić wyszukiwanie w głąb przed wędrowaniem po nieskończonej ścieżce, możemy użyć wyszukiwania z ograniczeniem w głąb, wersji wyszukiwania w głąb, w której podajemy limit głębokości l i traktujemy wszystkie węzły na głębokości tak, jakby nie miały następców (zobacz Rysunek 3.12. Złożoność czasowa to O(bl), a złożoność przestrzeni to O(bl). Niestety, jeśli dokonamy złego wyboru, algorytm nie zdoła znaleźć rozwiązania, czyniąc je ponownie niekompletnym.Aby uchronić wyszukiwanie w głąb przed wędrowaniem po nieskończonej ścieżce, możemy użyć wyszukiwania z ograniczeniem w głąb, wersji wyszukiwania w głąb, w której podajemy limit głębokości l i traktujemy wszystkie węzły na głębokości tak, jakby nie miały następców (Złożoność czasowa to O(bl), a złożoność przestrzeni to O(bl). Niestety, jeśli dokonamy złego wyboru, algorytm nie zdoła znaleźć rozwiązania, czyniąc je ponownie niekompletnym.

Pogłębianie iteracyjne i wyszukiwanie podobne do drzewa z ograniczeniem głębokości. Pogłębianie iteracyjne wielokrotnie stosuje wyszukiwanie o ograniczonej głębokości z rosnącymi limitami. Zwraca jeden z trzech różnych typów wartości: albo węzeł rozwiązania; lub awaria, gdy wyczerpała wszystkie węzły i udowodniła, że nie ma rozwiązania na żadnej głębokości; lub odcięcie, co oznacza, że rozwiązanie może znajdować się na głębokości większej niż l. Jest to algorytm wyszukiwania podobny do drzewa, który nie śledzi osiągniętych stanów, a zatem zużywa znacznie mniej pamięci niż wyszukiwanie „najlepsze pierwsze”, ale wiąże się z ryzykiem wielokrotnego odwiedzania tego samego stanu na różnych ścieżkach. Ponadto, jeśli kontrola IS-CYCLE nie sprawdza wszystkich cykli, algorytm może zostać złapany w pętlę. Ponieważ przeszukiwanie w głąb jest przeszukiwaniem podobnym do drzewa, nie możemy generalnie powstrzymać go przed marnowaniem czasu na nadmiarowe ścieżki, ale możemy wyeliminować cykle kosztem czasu obliczeniowego. Jeśli spojrzymy tylko na kilka ogniw w łańcuchu nadrzędnym, możemy złapać większość cykli; dłuższe cykle są obsługiwane przez ograniczenie głębokości. Czasami na podstawie znajomości problemu można wybrać dobry limit głębokości. Na przykład na mapie Rumunii znajduje się 20 miast. Dlatego l = 19 , jest poprawną granicą. Ale gdybyśmy dokładnie przestudiowali mapę, odkrylibyśmy, że do każdego miasta można dotrzeć z dowolnego innego miasta w maksymalnie 9 akcjach. Ta liczba, znana jako średnica grafu w przestrzeni stanów, daje nam lepszy limit głębokości, co prowadzi do bardziej wydajnego wyszukiwania z ograniczeniem głębokości. Jednak w przypadku większości problemów nie będziemy znać dobrego limitu głębokości, dopóki nie rozwiążemy problemu. Iteracyjne wyszukiwanie pogłębiające rozwiązuje problem wyboru dobrej wartości przez wypróbowanie wszystkich wartości: najpierw 0, potem 1, potem 2 itd., dopóki nie zostanie znalezione rozwiązanie lub wyszukiwanie z ograniczeniem wgłębnym zwraca wartość niepowodzenia, a nie wartość odcięcia . Algorytm pokazano na rysunku powyżej. Pogłębianie iteracyjne łączy wiele zalet wyszukiwania w głąb i wszerz. Podobnie jak wyszukiwanie w głąb, jego wymagania dotyczące pamięci są skromne: O(bd), gdy istnieje rozwiązanie, lub O(bm) w skończonych przestrzeniach stanów bez rozwiązania. Podobnie jak przeszukiwanie wszerz, pogłębianie iteracyjne jest optymalne dla problemów, w których wszystkie działania mają ten sam koszt i są kompletne w skończonych acyklicznych przestrzeniach stanów lub w dowolnej skończonej przestrzeni stanów, gdy sprawdzamy węzły pod kątem cykli na całej ścieżce. Złożoność czasowa wynosi O(bd), gdy istnieje rozwiązanie, lub O(bm), gdy nie ma. Każda iteracja iteracyjnego wyszukiwania pogłębiającego generuje nowy poziom, w taki sam sposób jak wyszukiwanie wszerz, ale wszerz robi to poprzez przechowywanie wszystkich węzłów w pamięci, podczas gdy pogłębianie iteracyjne robi to poprzez powtarzanie poprzednich poziomów, oszczędzając w ten sposób pamięć kosztem więcej czasu. Rysunek przedstawia cztery iteracje pogłębiania iteracyjnego wyszukiwania na drzewie wyszukiwania binarnego, gdzie rozwiązanie znajduje się w czwartej iteracji.
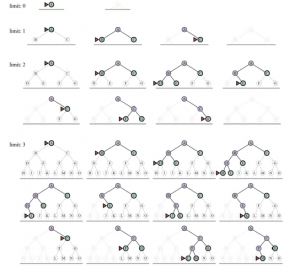
Cztery iteracje iteracyjnego pogłębiania poszukiwania celu M na drzewie binarnym, z limitem głębokości wahającym się od 0 do 3. Zauważ, że węzły wewnętrzne tworzą jedną ścieżkę. Trójkąt oznacza węzeł do rozwinięcia w następnej kolejności; zielone węzły z ciemnymi konturami znajdują się na granicy; bardzo słabe węzły prawdopodobnie nie mogą być częścią rozwiązania z tym ograniczeniem głębokości. Pogłębiające wyszukiwanie iteracyjne może wydawać się marnotrawstwem, ponieważ stany w górnej części drzewa wyszukiwania są wielokrotnie generowane ponownie. Ale dla wielu przestrzeni stanów większość węzłów znajduje się na dolnym poziomie, więc nie ma większego znaczenia, że górne poziomy się powtarzają. W iteracyjnym wyszukiwaniu pogłębiającym węzły na najniższym poziomie (głębokość ) są generowane raz, te na kolejnym poziomie są generowane dwukrotnie i tak dalej, aż do dzieci korzenia, które są generowane razy. Zatem całkowita liczba węzłów wygenerowanych w najgorszym przypadku wynosi
![]()
co daje złożoność czasową O(bd) – asymptotycznie taką samą jak przeszukiwanie wszerz. Na przykład, jeśli b = 10 i d = 5, liczby to
![]()
Jeśli naprawdę martwisz się powtarzaniem, możesz użyć podejścia hybrydowego, które uruchamia przeszukiwanie wszerz aż do zużycia prawie całej dostępnej pamięci, a następnie uruchamia iteracyjne pogłębianie ze wszystkich węzłów na granicy. Ogólnie rzecz biorąc, pogłębianie iteracyjne jest preferowaną metodą wyszukiwania bez informacji, gdy przestrzeń stanów wyszukiwania jest większa niż mieści się w pamięci, a głębokość rozwiązania nie jest znana.