Przeszukiwanie w głąb zawsze najpierw rozszerza najgłębszy węzeł na granicy. Może być wdrożony jako wezwanie do NAJLEPSZEJ PIERWSZEJ WYSZUKIWANIA, gdy funkcja oceny jest negatywna w stosunku do głębokości. Jednak jest to zwykle zaimplementowane nie jako przeszukiwanie grafów, ale jako przeszukiwanie przypominające drzewo, które nie przechowuje tabeli osiągniętych stanów. Postęp poszukiwań ilustruje Rysunek; wyszukiwanie przechodzi natychmiast do najgłębszego poziomu drzewa wyszukiwania, gdzie węzły nie mają następców. Wyszukiwanie następnie „cofa się” do następnego najgłębszego węzła, który wciąż ma nierozwiniętych następców. Wyszukiwanie w głąb nie jest optymalne pod względem kosztów; zwraca pierwsze znalezione rozwiązanie, nawet jeśli nie jest najtańsze.
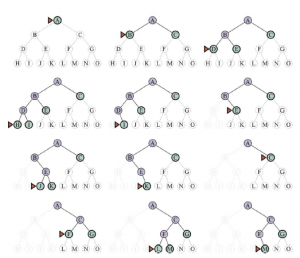
Kilkanaście kroków (od lewej do prawej, od góry do dołu) w trakcie przeszukiwania w głąb drzewa binarnego od stanu początkowego A do celu M. Granica jest zielona, z trójkątem oznaczającym węzeł, który ma zostać rozwinięty w następnej kolejności. Poprzednio rozwinięte węzły są lawendowe, a
potencjalne przyszłe węzły mają delikatne przerywane linie. Rozszerzone węzły bez potomków na granicy (bardzo słabe linie) można odrzucić.
Dla skończonych przestrzeni stanów, które są drzewami, jest wydajny i kompletny; w przypadku acyklicznych przestrzeni stanów może skończyć się wielokrotnym rozszerzaniem tego samego stanu różnymi ścieżkami, ale (ewentualnie) systematycznie bada całą przestrzeń. W cyklicznych przestrzeniach stanów może utknąć w nieskończonej pętli; dlatego niektóre implementacje wyszukiwania w głąb sprawdzają każdy nowy węzeł pod kątem cykli. Wreszcie, w nieskończonych przestrzeniach stanów przeszukiwanie w głąb nie jest systematyczne: może utknąć w nieskończonej ścieżce, nawet jeśli nie ma cykli. W związku z tym wyszukiwanie w głąb jest niekompletne. Przy tych wszystkich złych wiadomościach, dlaczego ktokolwiek miałby rozważać korzystanie z wyszukiwania w głąb, a nie wszerz lub w pierwszej kolejności? Odpowiedź jest taka, że w przypadku problemów, w których możliwe jest wyszukiwanie podobne do drzewa, wyszukiwanie w głąb ma znacznie mniejsze zapotrzebowanie na pamięć. W ogóle nie trzymamy ustalonego stołu, a granica jest bardzo mała: pomyśl o granicy w przeszukiwaniu wszerz jako powierzchni stale rozszerzającej się sfery, podczas gdy granica w przeszukiwaniu w głąb to tylko promień kula.
W przypadku skończonej przestrzeni stanów w kształcie drzewa, przeszukiwanie drzewa w głąb najpierw zajmuje czas proporcjonalny do liczby stanów i ma złożoność pamięci tylko O(b,m) , gdzie b jest czynnikiem rozgałęzienia a m jest maksymalną głębokością drzewo. Niektóre problemy, które wymagałyby eksabajtów pamięci przy przeszukiwaniu wszerz, można rozwiązać przy użyciu tylko kilobajtów przy użyciu przeszukiwania w głąb. Ze względu na oszczędne wykorzystanie pamięci, przeszukiwanie drzewa w głąb zostało przyjęte jako podstawowy koń pociągowy wielu obszarów sztucznej inteligencji, w tym spełniania ograniczeń, spełnialności zdań i programowania logicznego.
Wariant wyszukiwania w głąb, zwany wyszukiwaniem wstecznym, zużywa jeszcze mniej pamięci. Każdy częściowo rozwinięty węzeł zapamiętuje, który następnik wygenerować jako następny. Ponadto następniki są generowane przez bezpośrednią modyfikację opisu stanu bieżącego zamiast przydzielania pamięci dla zupełnie nowego stanu. Zmniejsza to wymagania dotyczące pamięci do tylko jednego opisu stanu i ścieżki działań O(m); znaczne oszczędności w stosunku do stanów O(bm) w przypadku wyszukiwania w głąb. W przypadku wycofywania mamy również możliwość utrzymywania wydajnej struktury danych dla stanów na bieżącej ścieżce, co pozwala nam na sprawdzanie ścieżki cyklicznej w czasie O(1), a nie O(m). Aby cofanie zadziałało, musimy być w stanie cofnąć każdą akcję, gdy się cofamy. . Cofanie się ma kluczowe znaczenie dla powodzenia wielu problemów z dużymi opisami stanów, takich jak montaż robotów.