Algorytm Dijkstry lub przeszukiwanie o jednolitym koszcie

Gdy akcje mają różne koszty, oczywistym wyborem jest użycie wyszukiwania „najlepszy-pierwszy”, gdzie funkcją oceny jest koszt ścieżki od korzenia do bieżącego węzła. Nazywa się to algorytmem Dijkstry przez społeczność informatyki teoretycznej i wyszukiwaniem jednolitych kosztów przez społeczność AI. Pomysł polega na tym, że podczas gdy wyszukiwanie wszerz rozprzestrzenia się falami o jednakowej głębokości, najpierw głębokości 1, potem głębokości 2, a zatem wyszukiwanie według jednolitego kosztu rozprzestrzenia się falami o jednakowych kosztach ścieżki. Algorytm może być zaimplementowany jako wywołanie BEST-FIRSTSEARCH z PATH-COST jako funkcją oceny.

Rozważmy rysunek , gdzie problemem jest dostanie się z Sibiu do Bukaresztu. Następcami Sibiu są Rimnicu Vilcea i Fagaras, z kosztami odpowiednio 80 i 99. Węzeł o najniższym koszcie, Rimnicu Vilcea, jest następnie rozbudowywany, dodając Pitesti z kosztem 80 = 97 = 177 .Węzeł o najniższym koszcie to teraz Fagaras, więc jest rozwijany, dodając Bukareszt z kosztem  99 + 211 = 310.Bukareszt jest celem, ale algorytm testuje cele tylko wtedy, gdy rozwija węzeł , a nie wtedy, gdy generuje węzeł, więc nie wykrył jeszcze, że jest to ścieżka do celu.

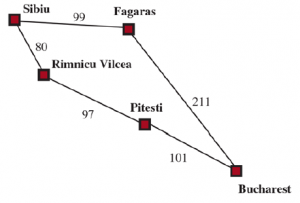
Algorytm kontynuuje, wybierając Pitesti jako następną ekspansję i dodając drugą ścieżkę do Bukaresztu z kosztem 80 + 97 + 101 = 278. Ma niższy koszt, więc zastępuje poprzednią ścieżkę w osiągniętym i jest dodawany do granicy. Okazuje się, że ten węzeł ma teraz najniższy koszt, więc jest uważany za następny, uznany za cel i zwrócony. Zauważ, że gdybyśmy sprawdzili cel przy generowaniu węzła, a nie podczas rozwijania węzła o najniższym koszcie, zwrócilibyśmy ścieżkę o wyższym koszcie (tę przez Fagarasa). Złożoność wyszukiwania o jednolitym koszcie jest scharakteryzowana C^* w kategoriach kosztu optymalnego rozwiązania a ϵ  dolnego ograniczenia kosztu każdego działania, przy czym ϵ > 0 Najgorsza złożoność czasowa i przestrzenna algorytmu jest znacznie większa niż b^d. Tak jest ponieważ wyszukiwanie o jednolitym koszcie może eksplorować duże drzewa działań o niskich kosztach przed zbadaniem ścieżek wiążących się z kosztownymi i być może użytecznymi działaniami. Gdy wszystkie koszty działań są równe to  b^d+1, przeszukiwanie jest sprawiedliwe i o jednolitym koszcie jest podobne do przeszukiwania wszerz. Wyszukiwanie o jednolitym koszcie jest kompletne i optymalne pod względem kosztów, ponieważ pierwsze znalezione rozwiązanie będzie miało koszt co najmniej tak niski, jak koszt każdego innego węzła na granicy. Wyszukiwanie o jednolitym koszcie systematycznie analizuje wszystkie ścieżki w kolejności rosnących kosztów, nigdy nie dając się złapać na jednej nieskończonej ścieżce (przy założeniu, że wszystkie koszty działania wynoszą > ϵ > 0 ).