Gdy wszystkie działania mają ten sam koszt, odpowiednią strategią jest przeszukiwanie wszerz, w którym najpierw rozwijany jest węzeł główny, następnie rozwijane są wszystkie następniki węzła głównego, następnie ich następcy i tak dalej. Jest to strategia systematycznego wyszukiwania, która jest zatem kompletna nawet w nieskończonych przestrzeniach stanów. Moglibyśmy zaimplementować wyszukiwanie wszerz jako wywołanie BEST-FIRST-SEARCH, gdzie funkcja oceny f(n) jest głębokością węzła — to znaczy liczbą działań, jakie trzeba wykonać, aby dotrzeć do węzła. Możemy jednak uzyskać dodatkową wydajność za pomocą kilku sztuczek. Kolejka typu pierwszy-w-pierwszy-wyszła będzie szybsza niż kolejka priorytetowa i da nam prawidłową kolejność węzłów: nowe węzły (które zawsze znajdują się głębiej niż ich rodzice) idą na tył kolejki, a stare węzły, które są płytsze niż nowe węzły, należy je najpierw rozszerzyć. Ponadto osiągnięty może być zbiór stanów, a nie mapowanie ze stanów na węzły, ponieważ po osiągnięciu stanu nigdy nie możemy znaleźć lepszej ścieżki do stanu. Oznacza to również, że możemy wykonać test wczesnego celu, sprawdzający, czy węzeł jest rozwiązaniem zaraz po jego wygenerowaniu, a nie test późnego celu, którego używa wyszukiwanie „najlepszy-pierwszy”, czekając, aż węzeł zostanie usunięty z kolejki. Rysunek przedstawia postęp w przeszukiwaniu wszerz w drzewie binarnym, a algorytm przedstawia algorytm z ulepszeniami wydajności wczesnego celu.


Wyszukiwanie wszerz zawsze znajduje rozwiązanie z minimalną liczbą akcji, ponieważ podczas generowania węzłów na głębokości d wygenerowało już wszystkie węzły na głębokości d-1, więc gdyby jeden z nich był rozwiązaniem, zostałoby znalezione. Oznacza to, że jest optymalny pod względem kosztów w przypadku problemów, w których wszystkie działania mają ten sam koszt, ale nie w przypadku problemów, które nie mają tej właściwości. W obu przypadkach jest kompletny. Pod względem czasu i przestrzeni wyobraź sobie poszukiwanie jednolitego drzewa, w którym każde państwo ma następców. Korzeń drzewa wyszukiwania generuje b węzłów, z których każdy generuje więcej węzłów, łącznie na drugim poziomie b2. Każdy z nich generuje więcej węzłów, dając b3węzły na trzecim poziomie i tak dalej. Załóżmy teraz, że rozwiązanie znajduje się na głębokości d. Wtedy łączna liczba wygenerowanych węzłów wynosi
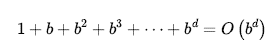
Wszystkie węzły pozostają w pamięci, więc zarówno czasowa, jak i przestrzenna złożoność O(bd) są wykładniczymi ograniczeniami, które są przerażające. Jako typowy przykład ze świata rzeczywistego rozważ problem z szybkością przetwarzania współczynnika b = 10, rozgałęzienia 1 milion węzłów na sekundę i wymaganiami dotyczącymi pamięci 1 KB/węzeł. Wyszukiwanie do głębokości d = 10 zajęłoby mniej niż 3 godziny, ale wymagałoby 10 terabajtów pamięci. Wymagania dotyczące pamięci stanowią większy problem dla wyszukiwania wszerz niż czas wykonania. Ale czas jest nadal ważnym czynnikiem. Na głębokości d = 14, nawet przy nieskończonej pamięci, poszukiwania zajęłyby 3,5 roku. Ogólnie, problemów związanych z wyszukiwaniem złożoności wykładniczej nie można rozwiązać przez niedoinformowane wyszukiwanie jakichkolwiek przypadków poza najmniejszymi.