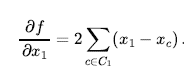Miesiąc: sierpień 2021

Wcześniej przyjęliśmy w pełni obserwowalne, deterministyczne, znane środowisko. Dzięki temu agent może obserwować stan początkowy, obliczać sekwencję działań, które prowadzą do celu i wykonywać je z „zamkniętymi oczami”, nigdy nie musząc używać swoich percepcji. Kiedy jednak środowisko jest częściowo obserwowalne, osoba nie wie na pewno, w jakim jest stanie; a gdy środowisko jest niedeterministyczne, agent nie wie, do jakiego stanu przechodzi po wykonaniu działania. Oznacza to, że zamiast myśleć „Jestem w stanie s1 i jeśli podejmę działanie, skończę w stanie s2 ”, agent będzie teraz myślał „Jestem w stanie s1 lub s3 , a jeśli podejmę działanie Skończę w stanie s2, s4 lub s5”. Zbiór stanów fizycznych, które według agenta są możliwe, nazywamy stanem przekonań. W środowiskach częściowo obserwowalnych i niedeterministycznych rozwiązanie problemu nie jest dłuższa sekwencja, ale raczej plan warunkowy (czasami nazywany planem awaryjnym lub strategią), który określa, co należy zrobić w zależności od tego, jakie percepty otrzymuje agent podczas wykonywania planu. W tej części zbadamy niedeterminizm, a w następnej częściową obserwowalność.

Wyjaśniliśmy różnicę między środowiskami dyskretnymi i ciągłymi, wskazując, że większość środowisk świata rzeczywistego jest ciągła. Ciągła przestrzeń działania ma nieskończony czynnik rozgałęzienia, a zatem nie może być obsłużona przez większość algorytmów, które omówiliśmy do tej pory (z wyjątkiem wspinaczki pod górę pierwszego wyboru i symulowanego wyżarzania). Ta sekcja zawiera bardzo krótkie wprowadzenie do niektórych lokalnych technik wyszukiwania spacji ciągłych. Literatura na ten temat jest obszerna; wiele podstawowych technik powstało w XVII wieku, po opracowaniu rachunku różniczkowego przez Newtona i Leibniza. Zastosowania tych technik znajdujemy w kilku miejscach tej książki, w tym w rozdziałach dotyczących uczenia się, wizji i robotyki. Zaczynamy od przykładu. Załóżmy, że chcemy umieścić trzy nowe lotniska w dowolnym miejscu w Rumunii, tak aby zminimalizować sumę kwadratów odległości w linii prostej od każdego miasta na mapie do najbliższego lotniska. Przestrzeń państwowa jest następnie definiowana przez współrzędne trzech lotnisk: (x₁,y₁) , (x₂,y₂) i (x₃,y₃). To jest sześciowymiarowa przestrzeń; mówimy również, że stany są definiowane przez sześć zmiennych. Ogólnie, stany są definiowane przez dwuwymiarowy wektor zmiennych, . Poruszanie się w tej przestrzeni odpowiada przesuwaniu jednego lub więcej lotnisk na mapie. Funkcja celu f(x) = f(x₁,y₁,x₂,y₂,x₃,y₃) jest stosunkowo łatwa do obliczenia dla dowolnego konkretnego stanu po obliczeniu najbliższych miast. Niech C_i będzie zbiorem miast, których najbliższym lotniskiem (w stanie x) jest lotnisko . Potem będzie

Równanie to jest poprawne nie tylko dla stanu, ale także dla stanów x w lokalnym sąsiedztwie x. Jednak globalnie nie jest to poprawne; jeśli oddalimy się zbyt daleko (zmieniając położenie jednego lub więcej lotnisk o dużą wartość), to zestaw najbliższych miast tego lotniska zmienia się i musimy ponownie obliczyć Ci . Jednym ze sposobów radzenia sobie z ciągłą przestrzenią stanów jest jej dyskretyzacja. Na przykład, zamiast pozwalać, aby lokalizacje (x₁,y₁) były dowolnymi punktami w ciągłej dwuwymiarowej przestrzeni, moglibyśmy ograniczyć je do stałych punktów na prostokątnej siatce z odstępami wielkości (delta). Wtedy zamiast nieskończonej liczby następców, każdy stan w przestrzeni miałby tylko 12 następców, co odpowiada zwiększeniu jednej z 6 zmiennych o +/-δ. Następnie możemy zastosować dowolny z naszych lokalnych algorytmów wyszukiwania do tej dyskretnej przestrzeni. Alternatywnie moglibyśmy uczynić czynnik rozgałęzienia skończony przez losowe próbkowanie stanów następczych, poruszając się w losowym kierunku o niewielką wartość, . Metody mierzące postęp poprzez zmianę wartości funkcji celu pomiędzy dwoma pobliskimi punktami nazywane są empirycznymi metodami gradientowymi. Empiryczne poszukiwanie gradientu jest tym samym, co wspinaczka po najbardziej stromych zboczach w dyskretnej wersji przestrzeni stanów. Zmniejszenie wartości w czasie może dać dokładniejsze rozwiązanie, ale niekoniecznie zbiega się do globalnego optimum w limicie.

Często mamy funkcję celu wyrażoną w postaci matematycznej, tak że możemy użyć rachunku różniczkowego do rozwiązania problemu analitycznie, a nie empirycznie. Wiele metod próbuje wykorzystać gradient krajobrazu, aby znaleźć maksimum. Gradient funkcji celu jest wektorem f, który podaje wielkość i kierunek najbardziej stromego zbocza. Na nasz problem mamy

W niektórych przypadkach możemy znaleźć maksimum, rozwiązując równanie . (Można to zrobić, na przykład, gdybyśmy umieścili tylko jedno lotnisko; rozwiązaniem jest średnia arytmetyczna wszystkich współrzędnych wszystkich miast.) Jednak w wielu przypadkach tego równania nie da się rozwiązać w postaci zamkniętej. Na przykład w przypadku trzech lotnisk wyrażenie określające gradient zależy od tego, które miasta znajdują się najbliżej każdego lotniska w obecnym stanie. Oznacza to, że możemy obliczyć gradient lokalnie (ale nie globalnie); na przykład,

Mając lokalnie poprawne wyrażenie dla gradientu, możemy wykonać wspinaczkę pod górę o najbardziej stromym wzniesieniu, aktualizując aktualny stan zgodnie ze wzorem

gdzie α (alfa) jest małą stałą często nazywaną wielkością kroku. Istnieje ogromna różnorodność metod dostosowywania α . Podstawowym problemem jest to, że jeśli α jest za mały, to wymaga zbyt wielu kroków; jeśli α jest zbyt duży, wyszukiwanie może przekroczyć maksimum. Technika przeszukiwania linii próbuje przezwyciężyć ten dylemat, rozszerzając bieżący kierunek gradientu — zwykle przez wielokrotne podwajanie α – aż do ponownego spadku. Punkt, w którym to nastąpi, staje się nowym stanem obecnym. Istnieje kilka szkół myślenia o tym, jak należy obrać nowy kierunek w tym momencie.

W przypadku wielu problemów najskuteczniejszym algorytmem jest czcigodna metoda Newtona-Raphsona. Jest to ogólna technika znajdowania pierwiastków funkcji, czyli rozwiązywania równań postaci g(x) = 0 . Działa poprzez obliczenie nowego oszacowania pierwiastka x zgodnie ze wzorem Newtona

Aby znaleźć maksimum lub minimum f, musimy znaleźć x takie, że gradient jest wektorem zerowym (tj.  ). Zatem g(x) we wzorze Newtona staje się   , a równanie uaktualniające można zapisać w postaci macierzowo-wektorowej jako

gdzie H_f(x) jest hesowską macierzą drugich pochodnych, której elementy H_ij są podane przez

. W naszym przykładzie z lotniskiem widzimy z równania , że H_f(x) jest szczególnie proste: elementy poza przekątną wynoszą zero, a elementy przekątne lotniska to tylko dwa razy więcej miast w C₁ . Chwilowe obliczenia pokazują, że jeden krok aktualizacji przenosi lotnisko bezpośrednio do środka ciężkości C_i, który jest minimum lokalnego wyrażenia dla f z równania (4.1) . Jednak w przypadku problemów wysokowymiarowych obliczenie n² wpisów hessu i odwrócenie go może być kosztowne, dlatego opracowano wiele przybliżonych wersji metody Newtona-Raphsona. Lokalne metody wyszukiwania cierpią z powodu lokalnych maksimów, grzbietów i płaskowyżów w przestrzeniach stanów ciągłych tak samo jak w przestrzeniach dyskretnych. Często pomocne są losowe restarty i symulowane wyżarzanie. Wysokowymiarowe przestrzenie ciągłe to jednak duże miejsca, w których bardzo łatwo się zgubić. Ostatnim tematem jest ograniczona optymalizacja. Problem optymalizacji jest ograniczony, jeśli rozwiązania muszą spełniać pewne twarde ograniczenia dotyczące wartości zmiennych. Na przykład, w naszym problemie z lokalizacją lotnisk, możemy ograniczyć lokalizację terenów na terenie Rumunii i na suchym lądzie (a nie w środku jezior). Trudność problemów optymalizacji z ograniczeniami zależy od charakteru ograniczeń i funkcji celu. Najbardziej znaną kategorią jest problem programowania liniowego, w którym ograniczenia muszą być nierównościami liniowymi tworzącymi zbiór wypukły, a funkcja celu jest również liniowa. Złożoność czasowa programowania liniowego jest wielomianowa w liczbie zmiennych. Programowanie liniowe jest prawdopodobnie najszerzej badaną i powszechnie przydatną metodą optymalizacji. Jest to szczególny przypadek bardziej ogólnego problemu optymalizacji wypukłej, który pozwala, aby obszarem ograniczeń był dowolny obszar wypukły, a celem była dowolna funkcja, która jest wypukła w obszarze ograniczeń. W pewnych warunkach wypukłe problemy optymalizacji są również rozwiązywalne wielomianowo i mogą być wykonalne w praktyce z tysiącami zmiennych. Kilka ważnych problemów związanych z uczeniem maszynowym i teorią sterowania można sformułować jako wypukłe problemy optymalizacji.

Teoria ewolucji została rozwinięta przez Karola Darwina w O powstawaniu gatunków za pomocą doboru naturalnego (1859) i niezależnie przez Alfreda Russela Wallace’a (1858). Główna idea jest prosta: w rozmnażaniu występują różnice i będą się one utrzymywały w kolejnych pokoleniach w przybliżeniu proporcjonalnie do ich wpływu na sprawność rozrodu. Teoria Darwina została opracowana bez wiedzy o tym, jak cechy organizmów mogą być dziedziczone i modyfikowane. Prawa probabilistyczne rządzące tymi procesami zostały po raz pierwszy zidentyfikowane przez Gregora Mendla (1866), mnicha, który eksperymentował ze słodkim groszkiem. Znacznie później Watson i Crick (1953) zidentyfikowali strukturę cząsteczki DNA i jej alfabet AGTC (adenina, guanina, tymina, cytozyna). W standardowym modelu zmienność występuje zarówno przez mutacje punktowe w sekwencji liter, jak i przez „crossover” (w którym DNA potomstwa jest generowane przez łączenie długich odcinków DNA od każdego rodzica). Analogia do lokalnych algorytmów wyszukiwania została już opisana; główną różnicą między poszukiwaniem wiązek stochastycznych a ewolucją jest użycie funkcji seksualnych i reprodukcja, w której następcy są generowani z wielu osobników, a nie tylko z jednej. Rzeczywiste mechanizmy ewolucji są jednak znacznie bogatsze, niż pozwala na to większość algorytmów genetycznych. Na przykład mutacje mogą obejmować odwrócenia, duplikacje i ruch dużych fragmentów DNA; niektóre wirusy pożyczają DNA z jednego organizmu i wstawiają go do innego; istnieją geny transpozycyjne, które nie robią nic poza kopiowaniem się tysiące razy w obrębie genomu. Istnieją nawet geny, które zatruwają komórki potencjalnych partnerów, które nie są nosicielami genu, zwiększając w ten sposób ich własne szanse na replikację. Najważniejszy jest fakt, że same geny kodują mechanizmy, dzięki którym genom jest reprodukowany i przenoszony do organizmu. W algorytmach genetycznych te mechanizmy są oddzielnym programem, który nie jest reprezentowany w manipulowanych ciągach. Ewolucja darwinowska może wydawać się nieefektywna, ponieważ na ślepo wygenerowała niektóre organizmy bez poprawy heurystyki wyszukiwania o jedną jotę. Ale uczenie się odgrywa rolę w ewolucji. Chociaż skądinąd wielki francuski przyrodnik Jean Lamarck (1809) mylił się, proponując, że cechy nabyte przez adaptację w ciągu życia organizmu zostaną przekazane jego potomstwu, pozornie podobna teoria Jamesa Baldwina (1896) jest słuszna: uczenie się może skutecznie rozluźnić przystosowanie. krajobraz, co prowadzi do przyspieszenia tempa ewolucji. Organizm, który ma cechę, która nie jest całkiem adaptacyjna do środowiska, przekaże tę cechę, jeśli ma również wystarczającą plastyczność, aby nauczyć się dostosowywać do środowiska w korzystny sposób. Symulacje komputerowe potwierdzają, że ten efekt Baldwina jest prawdziwy i że w konsekwencji rzeczy trudne do nauczenia trafiają do genomu, ale rzeczy łatwe do nauczenia nie muszą się tam znajdować.

Oczywiście efekt ten prawdopodobnie nie będzie znaczący, jeśli sąsiednie bity nie są ze sobą całkowicie powiązane, ponieważ wtedy będzie kilka ciągłych bloków, które zapewnią stałą korzyść. Algorytmy genetyczne działają najlepiej, gdy schematy odpowiadają znaczącym składnikom rozwiązania. Na przykład, jeśli ciąg jest reprezentacją anteny, wówczas schematy mogą reprezentować elementy anteny, takie jak reflektory i deflektory. Dobry element może być dobry w wielu różnych projektach. Sugeruje to, że skuteczne wykorzystanie algorytmów genetycznych wymaga starannej inżynierii reprezentacji. W praktyce algorytmy genetyczne mają swoje miejsce w szerokim krajobrazie metod optymalizacji , zwłaszcza w przypadku złożonych problemów strukturalnych, takich jak układ obwodów lub planowanie warsztatów, a ostatnio w ewolucji architektury głębokich sieci neuronowych . Nie jest jasne, na ile atrakcyjność algorytmów genetycznych wynika z ich wyższości w konkretnych zadaniach, a na ile z atrakcyjnej metafory ewolucji.

Algorytmy ewolucyjne można postrzegać jako warianty stochastycznego wyszukiwania wiązek, które są wyraźnie motywowane metaforą doboru naturalnego w biologii: istnieje populacja osobników (stanów), w której najsilniejsze (o najwyższej wartości) osobniki produkują potomstwo (stany następcze), które zaludnienie następnego pokolenia, proces zwany rekombinacją. Istnieje nieskończona liczba form algorytmów ewolucyjnych, różniących się w następujący sposób:

*Wielkość populacji.

*Reprezentacja każdej osoby. W algorytmach genetycznych każda osoba jest ciągiem nad skończonym alfabetem (często ciągiem logicznym), tak jak DNA jest ciągiem nad alfabetem ACGT. W strategiach ewolucyjnych jednostka jest sekwencją liczb rzeczywistych, a w programowaniu genetycznym jednostka jest programem komputerowym.

*Liczba mieszańców, która jest liczbą rodziców, którzy tworzą potomstwo. Najczęstszym przypadkiem jest ρ = 2: dwoje rodziców łączy swoje „geny” (części swojej reprezentacji), aby utworzyć potomstwo. Gdy ρ = 1 mamy stochastyczne przeszukiwanie wiązki (co może być postrzegane jako rozmnażanie bezpłciowe). Możliwe jest uzyskanie ρ > 2, co zdarza się rzadko w przyrodzie, ale jest wystarczająco łatwe do symulacji na komputerach.

*Proces selekcji osobników, które staną się rodzicami następnego pokolenia: jedną z możliwości jest wybór spośród wszystkich osobników z prawdopodobieństwem proporcjonalnym do ich wyniku sprawności. Inną możliwością jest losowe wybranie n osobników (n > ρ ), a następnie wybranie ρ najbardziej odpowiednich jako rodziców.

* Procedura rekombinacji. Jednym z powszechnych podejść (zakładając ρ = 2) jest losowy wybór punktu przecięcia w celu podzielenia każdego z ciągów rodzica i ponowne połączenie części w celu utworzenia dwojga dzieci, jednego z pierwszą częścią rodzica 1 i drugą częścią rodzica 2; druga z drugą częścią rodzica 1 i pierwszą częścią rodzica 2.

* Szybkość mutacji, która określa, jak często potomstwo ma losowe mutacje w swojej reprezentacji. Po wygenerowaniu potomstwa każdy bit w jego składzie jest odwracany z prawdopodobieństwem równym szybkości mutacji.

* Makijaż następnej generacji. Może to być tylko nowo uformowane potomstwo lub może obejmować kilku najlepszych rodziców z poprzedniego pokolenia (praktyka nazywana elitarnością, która gwarantuje, że ogólna sprawność nigdy nie spadnie z czasem). Praktyka uboju, w której odnotowuje się wszystkie osobniki poniżej określonego progu, prowadzi do przyspieszenia

Algorytm genetyczny, zilustrowany dla ciągów cyfr reprezentujących stany 8-królowych. Populacja początkowa w (a) jest uszeregowana według funkcji przystosowania w (b), w wyniku czego powstają pary do krycia w (c). Wytwarzają potomstwo w (d), które podlega mutacji w (e).

Rysunek (a) pokazuje populację czterech 8-cyfrowych ciągów, z których każdy reprezentuje stan układanki z ośmioma hetmanami: -ta cyfra reprezentuje numer rzędu hetmana w kolumnie . W (b) każdy stan jest oceniany przez funkcję sprawności. Wyższe wartości sprawności są lepsze, więc dla 8-problemu hetmanów używamy do rozwiązania liczby nieatakujących par hetmanów, która ma wartość 8 x 7/2 = 28. Wartości czterech stanów w (b) to 24, 23, 20 i 11. Oceny sprawności są następnie znormalizowane do prawdopodobieństw, a otrzymane wartości są pokazane obok wartości sprawności w (b).

Algorytm genetyczny, zilustrowany dla ciągów cyfr reprezentujących stany 8-królowych. Populacja początkowa w (a) jest uszeregowana według funkcji przystosowania w (b), w wyniku czego powstają pary do krycia w (c). Wytwarzają potomstwo w (d), które podlega mutacji w (e). W (c) wybiera się dwie pary rodziców zgodnie z prawdopodobieństwami z (b). Zauważ, że jedna osoba została wybrana dwukrotnie, a druga wcale. Dla każdej wybranej pary losowo wybierany jest punkt przecięcia (linia przerywana). W (d) krzyżujemy struny rodzicielskie w punktach przecięcia, dając nowe potomstwo. Na przykład pierwsze dziecko z pierwszej pary otrzymuje pierwsze trzy cyfry (327) od pierwszego rodzica, a pozostałe cyfry (48552) od drugiego rodzica. 8 stanów królowych biorących udział w tym etapie rekombinacji pokazano na rycinie

8 stanów matek odpowiadających dwóm pierwszym rodzicom z ryciny (c) i pierwszemu potomstwu z ryciny (d). Zielone kolumny są tracone w kroku krzyżowania, a czerwone kolumny pozostają. (Aby zinterpretować liczby na rysunku: wiersz 1 to wiersz dolny, a wiersz 8 to wiersz górny).

Wreszcie w (e) każda lokalizacja w każdym ciągu podlega losowej mutacji z małym niezależnym prawdopodobieństwem. Jedna cyfra została zmutowana u pierwszego, trzeciego i czwartego potomstwa. W zagadnieniu 8 hetmanów odpowiada to losowemu wybraniu hetmana i przesunięciu go na losowe pole w jego kolumnie. Często jest tak, że populacja jest zróżnicowana na wczesnym etapie procesu, więc krzyżowanie często wykonuje duże kroki w przestrzeni stanów na początku procesu wyszukiwania (jak w symulowanym wyżarzaniu). Po wielu pokoleniach selekcji w kierunku wyższej sprawności populacja staje się mniej zróżnicowana i typowe są mniejsze kroki. Rysunek  opisuje algorytm, który implementuje wszystkie te kroki.

Algorytmy genetyczne są podobne do stochastycznego wyszukiwania wiązki, ale z dodatkiem operacji krzyżowania. Jest to korzystne, jeśli istnieją bloki, które wykonują przydatne funkcje. Na przykład może się zdarzyć, że umieszczenie pierwszych trzech hetmanów w pozycjach 2, 4 i 6 (gdzie nie atakują się nawzajem) stanowi przydatny bloczek, który można połączyć z innymi przydatnymi bloczkami, które pojawiają się u innych osobników, aby skonstruować rozwiązanie . Można wykazać matematycznie, że jeśli bloki nie służą celowi – na przykład jeśli pozycje kodu genetycznego są losowo permutowane – to krzyżowanie nie daje żadnej korzyści. Teoria algorytmów genetycznych wyjaśnia, jak to działa, wykorzystując ideę schematu, który jest podciągiem, w którym niektóre pozycje można pozostawić nieokreślone. Na przykład schemat 246***** opisuje wszystkie stany 8-matek, w których pierwsze trzy królowe znajdują się odpowiednio na pozycjach 2, 4 i 6. Ciągi pasujące do schematu (takie jak 24613578) są nazywane instancjami schematu. Można wykazać, że jeśli średnia dopasowanie instancji schematu jest powyżej średniej, to liczba instancji schematu będzie z czasem rosła.

Utrzymywanie tylko jednego węzła w pamięci może wydawać się skrajną reakcją na problem ograniczeń pamięci. Lokalny algorytm wyszukiwania wiązki śledzi stany, a nie tylko jeden. Zaczyna się od losowo generowanych stanów. Na każdym kroku generowane są wszystkie następcy wszystkich stanów. Jeśli którykolwiek jest celem, algorytm zatrzymuje się. W przeciwnym razie wybiera najlepszych następców z pełnej listy i powtarza. Na pierwszy rzut oka lokalne przeszukiwanie wiązki ze stanami może wydawać się niczym innym, jak uruchamianiem k losowych restartów równolegle zamiast sekwencyjnie. W rzeczywistości te dwa algorytmy są zupełnie inne. W wyszukiwaniu z ponownym uruchomieniem losowym każdy proces wyszukiwania działa niezależnie od innych. W lokalnym wyszukiwaniu wiązki przydatne informacje są przekazywane między równoległymi wątkami wyszukiwania. W efekcie stany, które generują najlepszych następców, mówią innym: „Chodź tutaj, trawa jest bardziej zielona!” Algorytm szybko porzuca bezowocne poszukiwania i przenosi swoje zasoby tam, gdzie dokonuje się największy postęp. Lokalne wyszukiwanie wiązki może ucierpieć z powodu braku różnorodności między stanami – mogą one zostać skupione w małym regionie przestrzeni stanów, co sprawia, że ​​wyszukiwanie jest niewiele więcej niż -raz wolniejszą wersją wspinaczki górskiej. Wariant zwany poszukiwaniem stochastycznym, analogiczny do stochastycznego wspinania się po wzgórzach, pomaga złagodzić ten problem. Zamiast wybierać najlepszych następców, stochastyczne wyszukiwanie wiązki wybiera następców z prawdopodobieństwem proporcjonalnym do wartości następcy, zwiększając w ten sposób różnorodność.

 

Algorytm pokonywania wzniesień, który nigdy nie wykonuje ruchów „w dół” w kierunku stanów o niższej wartości (lub wyższym koszcie), jest zawsze podatny na utknięcie w lokalnym maksimum. W przeciwieństwie do tego, czysto losowe chodzenie, które przechodzi do stanu następcy bez troski o wartość, ostatecznie natknie się na globalne maksimum, ale będzie wyjątkowo nieefektywne. Dlatego rozsądne wydaje się połączenie wspinaczki pod górę z chodzeniem losowym w sposób, który zapewni zarówno efektywność, jak i kompletność. Takim algorytmem jest symulowane wyżarzanie. W metalurgii wyżarzanie jest procesem stosowanym do odpuszczania lub hartowania metali i szkła poprzez podgrzanie ich do wysokiej temperatury, a następnie stopniowe ich schładzanie, co pozwala na osiągnięcie przez materiał stanu krystalicznego o niskiej energii. Aby wyjaśnić symulowane wyżarzanie, zmieniamy nasz punkt widzenia ze wspinania się pod górę na schodzenie w dół (tj. minimalizując koszty) i wyobrażamy sobie zadanie wbicia piłki pingpongowej w najgłębszą szczelinę na bardzo wyboistej powierzchni. Jeśli po prostu pozwolimy piłce toczyć się, zatrzyma się ona na lokalnym minimum. Jeśli potrząśniemy powierzchnią, możemy wybić piłkę z lokalnego minimum – być może do głębszego lokalnego minimum, gdzie spędzi więcej czasu. Sztuką jest potrząsać wystarczająco mocno, aby wybić piłkę z lokalnych minimów, ale nie na tyle mocno, aby wybić ją z globalnego minimum. Roztwór do symulowanego wyżarzania ma rozpocząć się od mocnego wstrząsania (tj. w wysokiej temperaturze), a następnie stopniowo zmniejszać intensywność wytrząsania (tj. obniżać temperaturę). Ogólna struktura algorytmu symulowanego wyżarzania (rysunek 4.5 ) jest podobna do wspinaczki pod górę.

Jednak zamiast wybrać najlepszy ruch, wybiera losowy ruch. Jeśli posunięcie poprawia sytuację, jest zawsze akceptowane. W przeciwnym razie algorytm akceptuje ruch z pewnym prawdopodobieństwem mniejszym niż 1. Prawdopodobieństwo maleje wykładniczo wraz ze „złością” ruchu – wielkością ∆E, o którą ocena jest pogorszona. Prawdopodobieństwo maleje również wraz ze spadkiem „temperatury” T: „złe” ruchy są bardziej prawdopodobne na początku, gdy T jest wysokie, i stają się mniej prawdopodobne, gdy T maleje. Jeśli harmonogram obniży T do 0 wystarczająco wolno, to własność rozkładu Boltzmanna, e^∆E/T, polega na tym, że całe prawdopodobieństwo koncentruje się na globalnych maksimach, które algorytm znajdzie z prawdopodobieństwem bliskim 1. Symulowane wyżarzanie było używane do rozwiązywania problemów z układem VLSI począwszy od lat 80-tych. Jest szeroko stosowany w harmonogramach fabrycznych i innych zadaniach optymalizacyjnych na dużą skalę.

Algorytm wyszukiwania wspinaczki pokazano poniżej

Śledzi jeden aktualny stan i przy każdej iteracji przechodzi do sąsiedniego stanu o najwyższej wartości, to znaczy kieruje się w kierunku, który zapewnia najbardziej strome wznoszenie. Kończy się, gdy osiągnie „szczyt”, w którym żaden sąsiad nie ma wyższej wartości. Wspinaczka górska nie wykracza poza bezpośrednich sąsiadów obecnego stanu. Przypomina to próbę znalezienia szczytu Mount Everestu w gęstej mgle podczas cierpienia na amnezję. Zwróć uwagę, że jeden ze sposobów korzystania z wyszukiwania wspinaczki górskiej polega na użyciu negatywu heurystycznej funkcji kosztu jako funkcji celu; który będzie wspinał się lokalnie do stanu o najmniejszej heurystycznej odległości do celu. Aby zilustrować wspinaczkę po wzgórzach, użyjemy problemu 8-królowych.

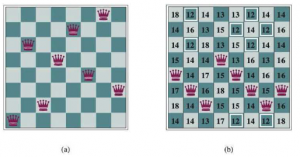
(a) Problem 8 hetmanów: umieść 8 hetmanów na szachownicy tak, aby żaden hetman nie atakował drugiego. (Hetman atakuje dowolną figurę w tym samym rzędzie, kolumnie lub po przekątnej.) Ta pozycja jest prawie rozwiązaniem, z wyjątkiem dwóch hetmanów w czwartej i siódmej kolumnie, które atakują się nawzajem po przekątnej. (b) Stan 8 hetmanów z heurystycznym kosztorysem h = 17. Plansza pokazuje wartość dla każdego możliwego następcy uzyskanego przez przesunięcie hetmana w jej kolumnie. Jest 8 ruchów, które są remisowane najlepiej, z h = 12 . Algorytm pokonywania wzniesień wybierze jeden z nich.

Użyjemy sformułowania pełnego stanu, co oznacza, że każdy stan ma wszystkie składniki rozwiązania, ale nie wszystkie mogą być we właściwym miejscu. W tym przypadku każdy stan ma na planszy 8 hetmanów, po jednej na kolumnę. Stan początkowy wybierany jest losowo, a następcami stanu są wszystkie możliwe stany generowane przez przeniesienie jednej hetmanki do innego pola w tej samej kolumnie (a więc każdy stan ma 8 x 7 = 56 następców). Heurystyczna funkcja kosztu to liczba par królowych, które atakują się nawzajem; będzie to zero tylko dla rozwiązań. (Liczy się jako atak, jeśli dwa pionki znajdują się w tej samej linii, nawet jeśli znajduje się między nimi pionek). Rysunek (b) pokazuje stan, w którym h = 17 . Rysunek przedstawia również wartości wszystkich jego następców.

Wspinaczka górska jest czasami nazywana chciwym poszukiwaniem lokalnym, ponieważ chwyta stan dobrego sąsiada, nie myśląc z wyprzedzeniem o tym, gdzie iść dalej. Chociaż chciwość jest uważana za jeden z siedmiu grzechów głównych, okazuje się, że algorytmy chciwości często działają całkiem nieźle. Wspinaczka po wzgórzach może szybko poczynić postępy w kierunku rozwiązania problemu, ponieważ zazwyczaj dość łatwo jest poprawić zły stan. Na przykład ze stanu z rysunku 4.3(b) wystarczy pięć kroków, aby osiągnąć stan z rysunku (a), który ma h = 1 i jest prawie rozwiązaniem. Niestety, wspinaczka górska może utknąć z jednego z następujących powodów:

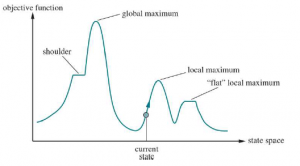
* LOCAL MAXIMA: Lokalne maksimum to szczyt, który jest wyższy niż każdy z sąsiednich stanów, ale niższy niż globalne maksimum. Algorytmy pokonywania wzniesień, które osiągną okolice lokalnego maksimum, zostaną przesunięte w górę w kierunku szczytu, ale utkną wtedy, nie mając dokąd pójść. Rysunek 4.1 ilustruje problem schematycznie. Mówiąc konkretniej, stan na rysunku 4.3(a) jest lokalnym maksimum (tj. lokalnym minimum kosztu); każdy ruch jednej hetmana pogarsza sytuację.

* GRZEBIE: Grzbiet pokazano na rysunku.

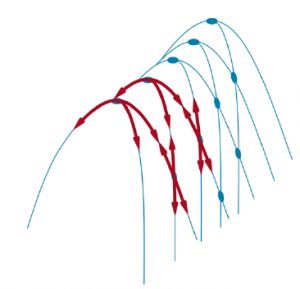
Ilustracja wyjaśniająca, dlaczego grzbiety utrudniają wspinaczkę na wzgórza. Siatka stanów (ciemne koła) nakłada się na grzbiet wznoszący się od lewej do prawej, tworząc ciąg lokalnych maksimów, które nie są bezpośrednio ze sobą połączone. Od każdego lokalnego maksimum wszystkie dostępne akcje kierują się w dół. Takie topologie są powszechne w niskowymiarowych przestrzeniach stanów, takich jak punkty na dwuwymiarowej płaszczyźnie. Ale w przestrzeniach stanów o setkach lub tysiącach wymiarów, ten intuicyjny obraz nie sprawdza się i zazwyczaj istnieje przynajmniej kilka wymiarów, które umożliwiają ucieczkę z grzbietów i płaskowyżów. Grzbiety tworzą sekwencję lokalnych maksimów, która jest bardzo trudna do nawigacji dla zachłannych algorytmów * PLATEAUS: Płaskowyż to płaski obszar krajobrazu przestrzeni stanów. Może to być płaskie maksimum lokalne, z którego nie ma wyjścia pod górę, lub pobocze, z którego możliwy jest postęp. Poszukiwanie wspinaczki może się zgubić wędrując po płaskowyżu.

W każdym przypadku algorytm osiąga punkt, w którym nie następuje żaden postęp. Zaczynając od losowo wygenerowanego stanu 8 królowych, wspinaczka na najbardziej strome wzgórze utknie w 86% przypadków, rozwiązując tylko 14% przypadków problemowych. Z drugiej strony działa szybko, wykonując średnio tylko 4 kroki, gdy się powiedzie, i 3, gdy utknie – nieźle jak na przestrzeń stanów z 8⁸ ≈ 17 milionami stanów. Jak możemy rozwiązać więcej problemów? Jedną z odpowiedzi jest pójście dalej, gdy osiągniemy plateau – aby pozwolić na ruch w bok w nadziei, że plateau jest naprawdę ramię . Ale jeśli faktycznie jesteśmy na płaskim lokalnym maksimum, to takie podejście będzie wędrować po płaskowyżu na zawsze. Dlatego możemy ograniczyć liczbę kolejnych ruchów w bok, zatrzymując się po, powiedzmy, 100 kolejnych ruchach w bok. Zwiększa to odsetek przypadków problemów rozwiązanych przez wspinaczkę pod górę z 14% do 94%. Sukces ma swoją cenę: algorytm średnio około 21 kroków dla każdego udanego wystąpienia i 64 dla każdego niepowodzenia.

Wynaleziono wiele wariantów wspinaczki górskiej. Wspinaczka stochastyczna wybiera losowo spośród ruchów pod górę; prawdopodobieństwo wyboru może się różnić w zależności od stromości podjazdu. Zwykle zbiega się to wolniej niż najbardziej strome podejście, ale w niektórych krajobrazach stanowych znajduje lepsze rozwiązania. Wspinaczka górska pierwszego wyboru wprowadza stochastyczne wspinanie się na wzniesienia poprzez losowe generowanie następców, dopóki nie zostanie wygenerowany jeden, który jest lepszy niż stan obecny. To dobra strategia, gdy państwo ma wielu (np. tysiące) następców.

Innym wariantem jest wspinaczka górska z losowym ponownym startem, która przyjmuje powiedzenie: „Jeśli na początku ci się nie uda, spróbuj, spróbuj ponownie”. Przeprowadza serię poszukiwań wspinaczkowych od losowo generowanych stanów początkowych, aż do znalezienia celu. Jest kompletny z prawdopodobieństwem 1, ponieważ ostatecznie wygeneruje stan docelowy jako stan początkowy. Jeśli każde wyszukiwanie wspinaczki ma prawdopodobieństwo powodzenia, oczekiwana liczba wymaganych ponownych uruchomień wynosi 1/p . W przypadku 8-kobietowych instancji bez dozwolonych ruchów na boki, p ≈ 14 , więc potrzebujemy około 7 iteracji, aby znaleźć cel (6 porażek i 1 sukces). Oczekiwana liczba kroków to koszt jednej udanej iteracji plus (1-p)/p razy koszt niepowodzenia, czyli łącznie około 22 kroki. Kiedy dopuszczamy ruchy boczne 1/0,94 ≈ 1,06, potrzebne są średnio iteracje i (1 x 21) + (0,06/0,94) x 64 ≈ 25 kroków. W przypadku 8-kobiet wspinanie się na wzgórze z losowym restartem jest naprawdę bardzo skuteczne. Nawet dla trzech milionów królowych podejście może znaleźć rozwiązanie w ciągu kilku sekund. Sukces wspinaczki górskiej zależy w dużej mierze od kształtu krajobrazu przestrzeni stanowej: jeśli jest niewiele lokalnych maksimów i płaskowyżów, wspinaczka górska z przypadkowym ponownym startem bardzo szybko znajdzie dobre rozwiązanie. Z drugiej strony, wiele prawdziwych problemów ma krajobraz, który bardziej przypomina rozsianą rodzinę łysiejących jeżozwierz na płaskiej podłodze, z miniaturowymi jeżozwierzami żyjącymi na czubku każdej igły jeżozwierza. Problemy NP-trudne mają wykładniczą liczbę lokalnych maksimów, na których można utknąć. Mimo to po niewielkiej liczbie ponownych uruchomień często można znaleźć dość dobre lokalne maksimum.

W problemach wyszukiwania  chcieliśmy znaleźć ścieżki w przestrzeni poszukiwań, takie jak droga z Aradu do Bukaresztu. Ale czasami zależy nam tylko na stanie końcowym, a nie na drodze do niego. Na przykład w zadaniu 8 hetmanów zależy nam tylko na znalezieniu poprawnej końcowej konfiguracji 8 hetmanów (ponieważ znając konfigurację, zrekonstruowanie kroków, które ją utworzyły, jest trywialne). Odnosi się to również do wielu ważnych aplikacji, takich jak projektowanie obwodów scalonych, rozplanowanie hali produkcyjnej, planowanie warsztatów, automatyczne programowanie, optymalizacja sieci telekomunikacyjnej, planowanie upraw i zarządzanie portfelem. Algorytmy wyszukiwania lokalnego działają poprzez przeszukiwanie od stanu początkowego do stanów sąsiednich, bez śledzenia ścieżek ani zbioru stanów, które zostały osiągnięte. Oznacza to, że nie są systematyczne – mogą nigdy nie zbadać części przestrzeni wyszukiwania, w której faktycznie znajduje się rozwiązanie. Mają jednak dwie kluczowe zalety: (1) zużywają bardzo mało pamięci; oraz (2) często potrafią znaleźć rozsądne rozwiązania w dużych lub nieskończonych przestrzeniach stanów, dla których systematyczne algorytmy są nieodpowiednie. Algorytmy wyszukiwania lokalnego mogą również rozwiązywać problemy optymalizacyjne, których celem jest znalezienie najlepszego stanu zgodnie z funkcją celu. Aby zrozumieć wyszukiwanie lokalne, rozważ stany problemu ułożone w krajobrazie przestrzeni stanów, jak pokazano na rysunku

Każdy punkt (stan) w krajobrazie ma „elewację”, określoną przez wartość funkcji celu. Jeśli wzniesienie odpowiada funkcji celu, wówczas celem jest znalezienie najwyższego szczytu – globalnego maksimum – a proces ten nazywamy wspinaczką górską. Jeśli wysokość odpowiada kosztowi, celem jest znalezienie najniższej doliny – globalnego minimum – i nazywamy to opadaniem gradientowym.

Wcześniejsze wpisy dotyczyły problemów w pełni obserwowalnych, deterministycznych, statycznych, znanych środowiskach, gdzie rozwiązaniem jest sekwencja działań. Tu rozluźniamy te ograniczenia. Zaczynamy od problemu znalezienia dobrego stanu bez martwienia się o ścieżkę do niego, obejmującego zarówno stany dyskretne , jak i ciągłe . Następnie rozluźniamy założenia determinizmu i obserwowalności .W niedeterministycznym świecie agent będzie potrzebował planu warunkowego i może wykonywać różne działania w zależności od tego, co obserwuje — na przykład zatrzymywanie, jeśli światło jest czerwone i wyłączanie, jeśli jest zielone. W przypadku częściowej obserwowalności agent będzie musiał również śledzić możliwe stany, w których może się znajdować. Na koniec, sekcja prowadzi agenta przez nieznaną przestrzeń, którą musi poznać w trakcie pracy, korzystając z wyszukiwania online.

Tu przedstawiono algorytmy wyszukiwania, których agent może używać do wybierania sekwencji działań w wielu różnych środowiskach – o ile są one epizodyczne, wykonywane przez jednego agenta, w pełni obserwowalne, deterministyczne, statyczne, dyskretne i całkowicie znane. Należy dokonać kompromisu między czasem potrzebnym na wyszukiwanie, ilością dostępnej pamięci i jakością rozwiązania. Możemy być bardziej wydajni, jeśli dysponujemy wiedzą zależną od dziedziny w postaci funkcji heurystycznej, która szacuje, jak daleko dany stan jest od celu, lub jeśli wstępnie obliczamy częściowe rozwiązania obejmujące wzorce lub punkty orientacyjne. Zanim agent będzie mógł rozpocząć poszukiwania, należy sformułować dobrze zdefiniowany problem. Problem składa się z pięciu części: stanu początkowego, zestawu działań, modelu przejścia opisującego wyniki tych działań, zestawu stanów celu oraz funkcji kosztu działania. Środowisko problemu jest reprezentowane przez graf w przestrzeni stanów. Rozwiązaniem jest ścieżka przez przestrzeń stanów (sekwencja działań) od stanu początkowego do stanu docelowego. Algorytmy wyszukiwania generalnie traktują stany i akcje jako niepodzielne, bez wewnętrznej struktury (chociaż wprowadziliśmy cechy stanów, gdy przyszedł czas na naukę). Algorytmy wyszukiwania są oceniane na podstawie kompletności, optymalności kosztów, złożoności czasowej i złożoności przestrzennej. Nieinformowane metody wyszukiwania mają dostęp tylko do definicji problemu. Algorytmy budują drzewo wyszukiwania, próbując znaleźć rozwiązanie. Algorytmy różnią się w zależności od tego, który węzeł rozwiną jako pierwszy:

– BEARTH-FIRST SEARCH wybiera węzły do ​​rozszerzenia za pomocą funkcji oceny.

–BEARTH-FIRST SEARCH rozwija najpierw najpłytsze węzły; jest kompletna, optymalna dla jednostkowych kosztów działania, ale ma wykładniczą złożoność przestrzeni.

– UNIFORM-COST SEARCH rozszerza węzeł o najniższym koszcie ścieżki g(n) i jest optymalny dla ogólnych kosztów działania.

– DEPTH-FIRST SEARCH rozszerza najgłębszy nierozwinięty węzeł  pierwszy. Nie jest ani kompletna, ani optymalna, ale ma liniową złożoność przestrzenną. Wyszukiwanie z ograniczeniem głębokości dodaje granicę głębokości.

– ITERATIVE DEEPENING SEARCH wywołuje wyszukiwanie w głąb z rosnącymi limitami głębokości, aż do znalezienia celu. Jest kompletny, gdy wykonywane jest sprawdzanie pełnego cyklu, optymalne dla kosztów działań jednostkowych, ma złożoność czasową porównywalną z przeszukiwaniem wszerz i ma liniową złożoność przestrzenną.

– WYSZUKIWANIE DWUKIERUNKOWE rozszerza dwie granice, jedną wokół stanu początkowego, a drugą wokół celu, zatrzymując się, gdy obie granice się spotykają.

*Poinformowane metody wyszukiwania mają dostęp do funkcji heurystycznej h(n), która szacuje koszt rozwiązania na podstawie n. Mogą mieć dostęp do dodatkowych informacji, takich jak bazy danych wzorców z kosztami rozwiązania.

– GREEDY BEST-FIRST SEARCH rozszerza węzły z minimalnym h(n). Nie jest optymalny, ale często jest skuteczny.

– A* SEARCH rozwija węzły o minimalnym f(n) = g(n) + h(n). A* jest zupełna i optymalna pod warunkiem, że h(n) jest dopuszczalne. Złożoność przestrzenna A* nadal stanowi problem dla wielu problemów.

– WYSZUKIWANIE DWUKIERUNKOWE A* jest czasami bardziej wydajne niż samo A*.

– IDA* (iterative deepening A* search) jest iteracyjną wersją pogłębiającą A*, a tym samym odnosi się do problemu złożoności przestrzeni.

– RBFS (rekurencyjne wyszukiwanie najlepsze-pierwsze) i SMA* (uproszczone A* ograniczone do pamięci) to niezawodne, optymalne algorytmy wyszukiwania, które wykorzystują ograniczoną ilość pamięci; mając wystarczająco dużo czasu, mogą rozwiązać problemy, dla których A* zabraknie pamięci.

– BEAM SEARCH ogranicza wielkość granicy; to sprawia, że ​​jest niekompletny i nieoptymalny, ale często znajduje dość dobre rozwiązania i działa szybciej niż pełne wyszukiwania.

– Wyszukiwanie z wagą A* koncentruje poszukiwania na celu, rozszerzając mniej węzłów, ale poświęcając optymalność.

* Wydajność algorytmów wyszukiwania heurystycznego zależy od jakości funkcji heurystycznej. Czasami można skonstruować dobrą heurystykę, rozluźniając definicję problemu, przechowując wstępnie obliczone koszty rozwiązania dla podproblemów w bazie danych wzorców, definiując punkty orientacyjne lub ucząc się na podstawie doświadczenia z klasą problemu.