Algorytm wyszukiwania przyjmuje problem wyszukiwania jako dane wejściowe i zwraca rozwiązanie lub wskazanie niepowodzenia. W tym rozdziale rozważymy algorytmy, które nakładają drzewo poszukiwań na graf przestrzeni stanów, tworząc różne ścieżki od stanu początkowego, próbując znaleźć ścieżkę, która osiąga stan docelowy. Każdy węzeł w drzewie wyszukiwania odpowiada stanowi w przestrzeni stanów, a krawędzie w drzewie wyszukiwania odpowiadają akcjom. Korzeń drzewa odpowiada początkowemu stanowi problemu. Ważne jest, aby zrozumieć różnicę między przestrzenią stanów a drzewem wyszukiwania. Przestrzeń stanów opisuje (prawdopodobnie nieskończony) zbiór stanów na świecie oraz działania, które umożliwiają przejście z jednego stanu do drugiego. Drzewo poszukiwań opisuje ścieżki pomiędzy tymi stanami, prowadzące do celu. Drzewo wyszukiwania może mieć wiele ścieżek do (a zatem wiele węzłów dla) dowolnego danego stanu, ale każdy węzeł w drzewie ma unikalną ścieżkę z powrotem do korzenia (jak we wszystkich drzewach). Rysunek przedstawia kilka pierwszych kroków na drodze do znalezienia drogi z Arad do Bukaresztu. Węzeł główny drzewa wyszukiwania znajduje się w stanie początkowym, Arad. Możemy rozwinąć węzeł, biorąc pod uwagę dostępne AKCJE dla tego stanu, używając funkcji RESULT, aby zobaczyć, dokąd te działania prowadzą, i generując nowy węzeł (nazywany węzłem potomnym lub węzłem następczym) dla każdego z wynikowych stanów. Każdy węzeł podrzędny ma Arad jako węzeł nadrzędny.
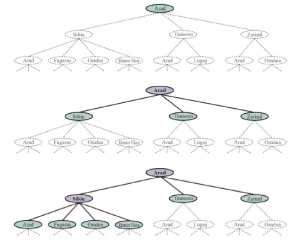
Trzy częściowe drzewa wyszukiwania do znalezienia trasy z Arad do Bukaresztu. Rozszerzone węzły są lawendowe z pogrubionymi literami; węzły na granicy, które zostały wygenerowane, ale jeszcze nie rozwinięte, są zielone; mówi się, że osiągnięto zbiór stanów odpowiadających tym dwóm typom węzłów. Węzły, które mogą zostać wygenerowane jako następne, są pokazane słabymi przerywanymi liniami. Zauważ, że w dolnym drzewie znajduje się cykl od Arad do Sibiu do Arad; to nie może być optymalna ścieżka, więc wyszukiwanie nie powinno być kontynuowane od tego miejsca.
Teraz musimy wybrać, który z tych trzech węzłów podrzędnych rozważymy w następnej kolejności. To jest esencja poszukiwań — śledzenie jednej opcji teraz i odłożenie pozostałych na później. Załóżmy, że najpierw zdecydujemy się rozwinąć Sibiu. Rysunek (na dole) pokazuje wynik: zestaw 6 nierozwiniętych węzłów (zaznaczonych pogrubioną czcionką). Nazywamy to granicą drzewa poszukiwań. Mówimy, że osiągnięto dowolny stan, w którym został wygenerowany węzeł (niezależnie od tego, czy ten węzeł został rozwinięty, czy nie). Rysunek poninżej przedstawia drzewo poszukiwań nałożone na wykres w przestrzeni stanów.
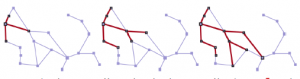
Sekwencja drzew wyszukiwania wygenerowana przez przeszukiwanie grafów problemu Rumunii. Na każdym etapie rozszerzyliśmy każdy węzeł na granicy, rozszerzając każdą ścieżkę o wszystkie stosowne działania, które nie prowadzą do stanu, który już został osiągnięty. Zauważ, że na trzecim etapie najwyżej położone miasto (Oradea) ma dwóch następców, do których obie zostały już osiągnięte innymi ścieżkami, więc żadne ścieżki nie są przedłużane z Oradei.
Zauważ, że granica oddziela dwa regiony grafu przestrzeni stanów: region wewnętrzny, w którym każdy stan został rozszerzony, oraz region zewnętrzny stanów, które jeszcze nie zostały osiągnięte. Ta właściwość jest zilustrowana na rysunku
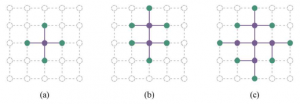
Własność separacji przeszukiwania grafów zilustrowana na zagadnieniu siatki prostokątnej. Granica (zielona) oddziela wnętrze (lawenda) od zewnętrza (słaba kreska). Granica to zbiór węzłów (i odpowiadających im stanów), które zostały osiągnięte, ale jeszcze nie rozwinięte; wnętrze to zbiór węzłów (i odpowiadających im stanów), które zostały rozwinięte; a zewnętrze to zestaw stanów, które nie zostały osiągnięte. W (a) tylko korzeń został rozszerzony. W (b) górny węzeł graniczny jest rozszerzony. W (c) pozostałe następcy korzenia są rozwinięte w kolejności zgodnej z ruchem wskazówek zegara.