Problem świata siatki to dwuwymiarowa prostokątna tablica kwadratowych komórek, w której agenci mogą przechodzić z komórki do komórki. Zazwyczaj agent może przemieszczać się do dowolnej wolnej od przeszkód sąsiedniej komórki – poziomo lub pionowo, aw niektórych problemach po przekątnej. Komórki mogą zawierać obiekty, które agent może podnieść, popchnąć lub w inny sposób działać; ściana lub inna nieprzejezdna przeszkoda w komórce uniemożliwia agentowi przejście do tej komórki. Świat próżni z sekcji wcześniejszej można sformułować jako problem świata siatki w następujący sposób:
* STANY: Stan świata mówi, które obiekty znajdują się w jakich komórkach. W świecie próżni obiekty są agentem i wszelkim brudem. W prostej wersji dwukomórkowej agent może znajdować się w jednej z dwóch komórek, a każde połączenie może zawierać brud lub nie, więc występują stany 2∙2∙2 = 8 (patrz Rysunek).
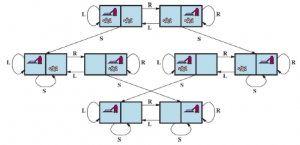
Ogólnie rzecz biorąc, środowisko próżniowe z n komórkami ma n∙2n stanów
* STAN POCZĄTKOWY: Dowolny stan może być wyznaczony jako stan początkowy.
* AKCJE: W świecie dwóch komórek zdefiniowaliśmy trzy akcje: ssanie, ruch w lewo i ruch w prawo. W dwuwymiarowym, wielokomórkowym świecie potrzebujemy więcej akcji ruchowych. Moglibyśmy dodać W górę i W dół, dając nam cztery bezwzględne akcje ruchu, lub moglibyśmy przełączyć się na akcje egocentryczne, zdefiniowane w odniesieniu do punktu widzenia agenta, na przykład: Do przodu, Do tyłu, Skręć w prawo i Skręć w lewo.
* MODEL PRZEJŚCIOWY: Ssanie usuwa wszelkie zabrudzenia z komórki agenta; Naprzód przesuwa agenta do przodu o jedną komórkę w kierunku, w którym jest zwrócony, chyba że uderzy w ścianę, w którym to przypadku akcja nie ma żadnego efektu. Wstecz przesuwa agenta w przeciwnym kierunku, podczas gdy skręty w prawo i skręty w lewo zmieniają kierunek, w którym jest zwrócony o 90o
* STANY CELÓW: Stany, w których każda komórka jest czysta.
* KOSZT AKCJI: Każda akcja kosztuje 1.
Innym rodzajem świata gridowego jest łamigłówka sokoban, w której celem agenta jest zepchnięcie szeregu pudełek rozsianych po siatce do wyznaczonych miejsc przechowywania. Na komórkę może przypadać najwyżej jedno pudełko. Gdy agent przechodzi do komórki zawierającej pudełko, a po drugiej stronie pudełka znajduje się pusta komórka, zarówno pudełko, jak i agent poruszają się do przodu. Agent nie może wepchnąć pudełka do innego pudełka lub ściany. W świecie z n komórkami i b pudełkami bez przeszkód istnieją n x n! / b!(n-b!) stany; na przykład na siatce 8 x 8 z tuzinem pudełek jest ponad 200 bilionów stanów. W układance z przesuwanymi płytkami wiele płytek (czasami nazywanych blokami lub kawałkami) jest ułożonych w siatkę z jednym lub więcej pustymi miejscami, tak aby niektóre płytki mogły wsunąć się w pustą przestrzeń. Jednym z wariantów jest łamigłówka Godziny szczytu, w której samochody i ciężarówki ślizgają się po siatce 6 x 6 , próbując uwolnić samochód z korka. Być może najbardziej znanym wariantem jest 8-puzzle (patrz Rysunek ), która składa się z siatki z ośmioma ponumerowanymi płytkami i jednym pustym polem oraz 15-puzle na siatce 4 x 4.
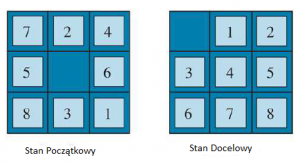
Celem jest osiągnięcie określonego stanu docelowego, takiego jak ten pokazany po prawej stronie rysunku. Standardowe sformułowanie 8 puzzli jest następujące:
* STANY: Opis stanu określa położenie każdej z płytek.
* STAN POCZĄTKOWY: Dowolny stan może być wyznaczony jako stan początkowy. Zauważ, że właściwość parzystości dzieli przestrzeń stanów – każdy cel można osiągnąć dokładnie z połowy możliwych stanów początkowych.
* AKCJE: Podczas gdy w świecie fizycznym jest to kafel, który się przesuwa, najprostszym sposobem opisania akcji jest myślenie o pustym miejscu poruszającym się w lewo, w prawo, w górę lub w dół. Jeśli półfabrykat znajduje się na krawędzi lub rogu, nie wszystkie działania będą miały zastosowanie.
* MODEL PRZEJŚCIOWY: Odwzorowuje stan i akcję na stan wynikowy; na przykład, jeśli zastosujemy Lewo do stanu początkowego na rysunku , wynikowy stan ma zamienione 5 i puste pole.
* STAN CELOWY: Chociaż każdy stan może być celem, zazwyczaj określamy stan za pomocą liczb w kolejności
* KOSZT AKCJI: Każda akcja kosztuje 1.
Zauważ, że każde sformułowanie problemu zawiera abstrakcje. Obszary składające się z 8 zagadek są skupione na ich początkowych i końcowych stanach, ignorując pośrednie miejsca, w których kafelek się przesuwa. Wyodrębniliśmy działania, takie jak potrząsanie płytą, gdy płytki utkną, i wykluczyliśmy wyrywanie płytek nożem i ponowne ich odkładanie. Pozostaje nam opis zasad, unikając wszelkich szczegółów fizycznych manipulacji. Nasz ostateczny ustandaryzowany problem został opracowany przez Donalda Knutha (1964) i ilustruje, jak mogą powstawać nieskończone przestrzenie stanów. Knuth przypuszczał, że począwszy od liczby 4, ciąg operacji pierwiastka kwadratowego, podłogi i silni może osiągnąć dowolną liczbę całkowitą dodatnią. Na przykład możemy osiągnąć 5 z 4 w następujący sposób:
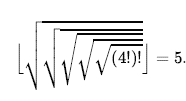
Definicja problemu jest prosta:
* STAN: Dodatnie liczby rzeczywiste.
* STAN POCZĄTKOWY: 4.
* DZIAŁANIA: Zastosuj pierwiastek kwadratowy, dolny lub silnię (silnia tylko dla liczb całkowitych).
* MODEL PRZEJŚCIOWY: Zgodnie z matematycznymi definicjami operacji.
* STAN DOCELOWY: Żądana dodatnia liczba całkowita.
* KOSZT AKCJI: Każda akcja kosztuje 1.
Przestrzeń stanów dla tego problemu jest nieskończona: dla dowolnej liczby całkowitej większej niż 2 operator silni zawsze da większą liczbę całkowitą. Problem jest interesujący, ponieważ bada bardzo duże liczby: najkrótsza droga do 5 prowadzi przez (4!)! = 620,448,401,733,239,439,360,000. Nieskończone przestrzenie stanów pojawiają się często w zadaniach związanych z generowaniem wyrażeń matematycznych, obwodów, dowodów, programów i innych obiektów definiowanych rekurencyjnie.