Miesiąc: lipiec 2021

Zanim przejdziemy do projektowania różnych algorytmów wyszukiwania, rozważymy kryteria wyboru spośród nich. Możemy ocenić wydajność algorytmu na cztery sposoby:

* KOMPLETNOŚĆ: Czy algorytm gwarantuje znalezienie rozwiązania, gdy jest, i prawidłowe zgłoszenie awarii, gdy nie ma?

* OPTYMALNOŚĆ KOSZTÓW: Czy znajduje rozwiązanie o najniższym koszcie ścieżki ze wszystkich rozwiązań?

* ZŁOŻONOŚĆ CZASOWA: Ile czasu zajmuje znalezienie rozwiązania? Można to zmierzyć w sekundach lub bardziej abstrakcyjnie na podstawie liczby rozważanych stanów i działań.

* KOMPLEKSOWOŚĆ PRZESTRZENI: Ile pamięci potrzeba do przeprowadzenia wyszukiwania?

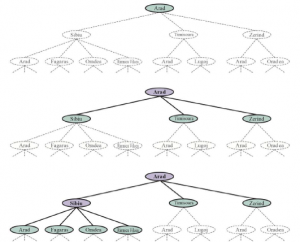
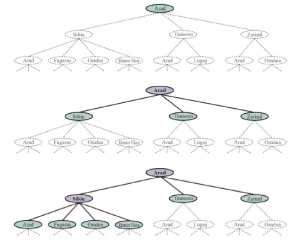
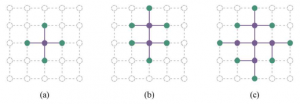
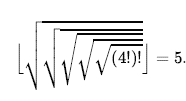
Aby zrozumieć kompletność, rozważ problem wyszukiwania z jednym celem. Ten cel może znajdować się w dowolnym miejscu w przestrzeni stanów; dlatego kompletny algorytm musi być w stanie systematycznie badać każdy stan, który jest osiągalny ze stanu początkowego. W skończonych przestrzeniach stanów, które są proste do osiągnięcia: tak długo, jak śledzimy ścieżki i odcinamy te, które są cyklami (np. Arad do Sibiu do Arad), w końcu dotrzemy do każdego osiągalnego stanu. W nieskończonych przestrzeniach stanów konieczna jest większa ostrożność. Na przykład algorytm, który wielokrotnie stosował operator „silnia” w zadaniu „4” Knutha, podążałby nieskończoną ścieżką od 4 do 4! do (4!)!, i tak dalej. Podobnie, na nieskończonej siatce bez przeszkód, wielokrotne poruszanie się do przodu w linii prostej również podąża nieskończoną ścieżką nowych stanów. W obu przypadkach algorytm nigdy nie powraca do stanu, który osiągnął wcześniej, ale jest niekompletny, ponieważ nigdy nie dochodzi do szerokich przestrzeni stanów. Aby być kompletnym, algorytm wyszukiwania musi być systematyczny w sposobie eksploracji nieskończonej przestrzeni stanów, upewniając się, że może ostatecznie osiągnąć dowolny stan, który jest połączony ze stanem początkowym. Na przykład w nieskończonej siatce jednym rodzajem systematycznego wyszukiwania jest spiralna ścieżka, która obejmuje wszystkie komórki znajdujące się kilka kroków od początku przed przejściem do komórek znajdujących się kilka kroków dalej. Niestety, w nieskończonej przestrzeni stanów bez rozwiązania, algorytm dźwięku musi kontynuować poszukiwania w nieskończoność; nie może zakończyć, ponieważ nie może wiedzieć, czy następny stan będzie celem.

Złożoność czasowa i przestrzenna jest rozpatrywana w odniesieniu do pewnej miary trudności problemu. W informatyce teoretycznej typową miarą jest rozmiar grafu w przestrzeni stanów |V| + |E|, gdzie |V| jest liczbą wierzchołków (węzłów stanu) grafu a |E| liczbą krawędzi (różnych par stan/działanie). Jest to właściwe, gdy wykres jest wyraźną strukturą danych, taką jak mapa Rumunii. Ale w wielu problemach AI graf jest reprezentowany tylko domyślnie przez stan początkowy, działania i model przejścia. W przypadku niejawnej przestrzeni stanów złożoność można mierzyć pod względem głębokości  d lub liczby działań w optymalnym rozwiązaniu; maksymalna liczba akcji na dowolnej ścieżce m ; oraz współczynnik rozgałęzienia b lub liczbę następców węzła, które należy wziąć pod uwagę.

Drzewo wyszukiwania pokazane na rysunku  (na dole) zawiera ścieżkę z Arad do Sibiu iz powrotem do Arad. Mówimy, że Arad jest powtarzającym się stanem w drzewie wyszukiwania, generowanym w tym przypadku przez cykl (znany również jako ścieżka zapętlona). Tak więc, mimo że przestrzeń stanów ma tylko 20 stanów, pełne drzewo poszukiwań jest nieskończone, ponieważ nie ma ograniczeń co do częstotliwości przechodzenia przez pętlę.

Po drugie, nie możemy się martwić o powtórzenie przeszłości. Istnieją pewne sformułowania problemów, w których rzadko lub niemożliwie dwie ścieżki osiągają ten sam stan. Przykładem może być problem z montażem, w którym każda akcja dodaje część do rozwijającego się złożenia i istnieje kolejność części tak, że można dodać, a potem, ale nie, a potem. W przypadku tych problemów możemy zaoszczędzić miejsce w pamięci, jeśli nie , nie śledź osiągniętych stanów i nie sprawdzamy nadmiarowych ścieżek. Algorytm wyszukiwania nazywamy przeszukiwaniem grafu, jeśli sprawdza on nadmiarowe ścieżki, a wyszukiwaniem podobnym do drzewa, jeśli nie sprawdza. Algorytm BEST-FIRST-SEARCH jest algorytmem przeszukiwania grafów; jeśli usuniemy wszystkie odniesienia, do których się udało, otrzymamy wyszukiwanie podobne do drzewa, które zużywa mniej pamięci, ale bada nadmiarowe ścieżki do tego samego stanu, a zatem będzie działać wolniej.

Po trzecie, możemy pójść na kompromis i sprawdzić cykle, ale ogólnie nie pod kątem nadmiarowych ścieżek. Ponieważ każdy węzeł ma łańcuch wskaźników nadrzędnych, możemy sprawdzić cykle bez potrzeby dodatkowej pamięci, podążając za łańcuchem rodziców, aby sprawdzić, czy stan na końcu ścieżki pojawił się wcześniej w ścieżce. Niektóre implementacje podążają za tym łańcuchem aż do góry, a tym samym eliminują wszystkie cykle; inne implementacje podążają tylko za kilkoma linkami (np. do rodzica, dziadka i pradziadka), a zatem zajmują tylko stałą ilość czasu, eliminując wszystkie krótkie cykle (i polegając na innych mechanizmach radzenia sobie z długimi cyklami).

Algorytmy wyszukiwania wymagają struktury danych do śledzenia drzewa wyszukiwania. Węzeł w drzewie jest reprezentowany przez strukturę danych z czterema komponentami:

* node.STATE: stan, któremu odpowiada węzeł;

* node.PARENT: węzeł w drzewie, który wygenerował ten węzeł;

* node.ACTION: akcja, która została zastosowana do stanu rodzica w celu wygenerowania tego węzła;

* node.PATH-COST: całkowity koszt ścieżki od stanu początkowego do tego węzła. We wzorach matematycznych używamy g(węzeł) jako synonimu PATH-COST.

Podążanie za wskaźnikami PARENT z powrotem z węzła pozwala nam odzyskać stany i działania na ścieżce do tego węzła. Robienie tego z węzła celu daje nam rozwiązanie. Potrzebujemy struktury danych do przechowywania granicy. Właściwym wyborem jest jakaś kolejka, ponieważ operacje na granicy to:

* IS-EMPTY(frontier) zwraca wartość true tylko wtedy, gdy na granicy nie ma żadnych węzłów.

* POP(frontier) usuwa górny węzeł z granicy i zwraca go.

* TOP(granica) zwraca (ale nie usuwa) górny węzeł granicy.

* ADD(node, frontier) wstawia węzeł we właściwe miejsce w kolejce.

W algorytmach wyszukiwania wykorzystywane są trzy rodzaje kolejek:

* Kolejka priorytetowa najpierw wyskakuje węzeł z minimalnym kosztem zgodnie z funkcją oceny f. Jest używany w wyszukiwaniu „najlepszy-pierwszy”.

* Kolejka FIFO lub kolejka pierwszy-w-pierwszy-wyjściowy najpierw wyskakuje węzeł, który został dodany do kolejki jako pierwszy; zobaczymy, że jest używany w przeszukiwaniu wszerz.

* Kolejka LIFO lub kolejka ostatnia-pierwsza-pierwsza (znana również jako stos) wyskakuje jako pierwszy ostatnio dodany węzeł; zobaczymy, że jest używany w poszukiwaniach dogłębnych.

Osiągnięte stany mogą być przechowywane jako tablica przeglądowa (np. tablica mieszająca), w której każdy klucz jest stanem, a każda wartość jest węzłem dla tego stanu.

Jak decydujemy, który węzeł z granicy będzie dalej rozszerzany? Bardzo ogólne podejście nazywa się przeszukiwaniem „najlepszy-pierwszy”, w którym wybieramy węzeł n , z minimalną wartością pewnej funkcji oceny f(n). Rysunek przedstawia algorytm. W każdej iteracji wybieramy węzeł na granicy z minimalną wartością f(n), zwracamy go, jeśli jego stan jest stanem docelowym, a w przeciwnym razie stosujemy EXPAND do generowania węzłów podrzędnych. Każdy węzeł podrzędny jest dodawany do granicy, jeśli nie został wcześniej osiągnięty, lub jest dodawany ponownie, jeśli jest teraz osiągany ścieżką, która ma niższy koszt ścieżki niż jakakolwiek poprzednia ścieżka. Algorytm zwraca albo wskazanie niepowodzenia, albo węzeł reprezentujący ścieżkę do celu. Stosując różne funkcje f(n), otrzymujemy różne specyficzne algorytmy, które omówimy.

Algorytm wyszukiwania przyjmuje problem wyszukiwania jako dane wejściowe i zwraca rozwiązanie lub wskazanie niepowodzenia. W tym rozdziale rozważymy algorytmy, które nakładają drzewo poszukiwań na graf przestrzeni stanów, tworząc różne ścieżki od stanu początkowego, próbując znaleźć ścieżkę, która osiąga stan docelowy. Każdy węzeł w drzewie wyszukiwania odpowiada stanowi w przestrzeni stanów, a krawędzie w drzewie wyszukiwania odpowiadają akcjom. Korzeń drzewa odpowiada początkowemu stanowi problemu. Ważne jest, aby zrozumieć różnicę między przestrzenią stanów a drzewem wyszukiwania. Przestrzeń stanów opisuje (prawdopodobnie nieskończony) zbiór stanów na świecie oraz działania, które umożliwiają przejście z jednego stanu do drugiego. Drzewo poszukiwań opisuje ścieżki pomiędzy tymi stanami, prowadzące do celu. Drzewo wyszukiwania może mieć wiele ścieżek do (a zatem wiele węzłów dla) dowolnego danego stanu, ale każdy węzeł w drzewie ma unikalną ścieżkę z powrotem do korzenia (jak we wszystkich drzewach). Rysunek  przedstawia kilka pierwszych kroków na drodze do znalezienia drogi z Arad do Bukaresztu. Węzeł główny drzewa wyszukiwania znajduje się w stanie początkowym, Arad. Możemy rozwinąć węzeł, biorąc pod uwagę dostępne AKCJE dla tego stanu, używając funkcji RESULT, aby zobaczyć, dokąd te działania prowadzą, i generując nowy węzeł (nazywany węzłem potomnym lub węzłem następczym) dla każdego z wynikowych stanów. Każdy węzeł podrzędny ma Arad jako węzeł nadrzędny.

Trzy częściowe drzewa wyszukiwania do znalezienia trasy z Arad do Bukaresztu. Rozszerzone węzły są lawendowe z pogrubionymi literami; węzły na granicy, które zostały wygenerowane, ale jeszcze nie rozwinięte, są zielone; mówi się, że osiągnięto zbiór stanów odpowiadających tym dwóm typom węzłów. Węzły, które mogą zostać wygenerowane jako następne, są pokazane słabymi przerywanymi liniami. Zauważ, że w dolnym drzewie znajduje się cykl od Arad do Sibiu do Arad; to nie może być optymalna ścieżka, więc wyszukiwanie nie powinno być kontynuowane od tego miejsca.

Teraz musimy wybrać, który z tych trzech węzłów podrzędnych rozważymy w następnej kolejności. To jest esencja poszukiwań — śledzenie jednej opcji teraz i odłożenie pozostałych na później. Załóżmy, że najpierw zdecydujemy się rozwinąć Sibiu. Rysunek (na dole) pokazuje wynik: zestaw 6 nierozwiniętych węzłów (zaznaczonych pogrubioną czcionką). Nazywamy to granicą drzewa poszukiwań. Mówimy, że osiągnięto dowolny stan, w którym został wygenerowany węzeł (niezależnie od tego, czy ten węzeł został rozwinięty, czy nie). Rysunek poninżej przedstawia drzewo poszukiwań nałożone na wykres w przestrzeni stanów.

Sekwencja drzew wyszukiwania wygenerowana przez przeszukiwanie grafów problemu Rumunii. Na każdym etapie rozszerzyliśmy każdy węzeł na granicy, rozszerzając każdą ścieżkę o wszystkie stosowne działania, które nie prowadzą do stanu, który już został osiągnięty. Zauważ, że na trzecim etapie najwyżej położone miasto (Oradea) ma dwóch następców, do których obie zostały już osiągnięte innymi ścieżkami, więc żadne ścieżki nie są przedłużane z Oradei.

Zauważ, że granica oddziela dwa regiony grafu przestrzeni stanów: region wewnętrzny, w którym każdy stan został rozszerzony, oraz region zewnętrzny stanów, które jeszcze nie zostały osiągnięte. Ta właściwość jest zilustrowana na rysunku

Własność separacji przeszukiwania grafów zilustrowana na zagadnieniu siatki prostokątnej. Granica (zielona) oddziela wnętrze (lawenda) od zewnętrza (słaba kreska). Granica to zbiór węzłów (i odpowiadających im stanów), które zostały osiągnięte, ale jeszcze nie rozwinięte; wnętrze to zbiór węzłów (i odpowiadających im stanów), które zostały rozwinięte; a zewnętrze to zestaw stanów, które nie zostały osiągnięte. W (a) tylko korzeń został rozszerzony. W (b) górny węzeł graniczny jest rozszerzony. W (c) pozostałe następcy korzenia są rozwinięte w kolejności zgodnej z ruchem wskazówek zegara.

Widzieliśmy już, jak definiowany jest problem znajdowania trasy pod kątem określonych lokalizacji i przejść wzdłuż krawędzi między nimi. Algorytmy wyszukiwania tras są używane w różnych aplikacjach. Niektóre, takie jak witryny internetowe i systemy samochodowe, które podają wskazówki dojazdu, są stosunkowo prostymi rozszerzeniami przykładu rumuńskiego. (Głównymi komplikacjami są różne koszty wynikające z opóźnień zależnych od ruchu oraz zmiany trasy z powodu zamknięcia dróg). Inne, takie jak przesyłanie strumieni wideo w sieciach komputerowych, planowanie operacji wojskowych i systemy planowania podróży lotniczych, wymagają znacznie bardziej złożonych specyfikacji. Rozważ problemy związane z podróżami lotniczymi, które muszą zostać rozwiązane przez witrynę internetową do planowania podróży:

* STANY: Każdy stan zawiera oczywiście lokalizację (np. lotnisko) i aktualny czas. Ponadto, ponieważ koszt działania (segment lotu) może zależeć od poprzednich segmentów, ich baz taryfowych oraz ich statusu jako krajowego lub międzynarodowego, państwo musi rejestrować dodatkowe informacje o tych „historycznych” aspektach.

STAN POCZĄTKOWY: Lotnisko macierzyste użytkownika.

CZYNNOŚCI: Wybierz dowolny lot z bieżącej lokalizacji, w dowolnej klasie miejsc, wylatując po aktualnym czasie, pozostawiając w razie potrzeby wystarczającą ilość czasu na transfer wewnątrz lotniska.

MODEL PRZEJŚCIOWY: Stan wynikający z odbycia lotu będzie miał miejsce docelowe lotu jako nową lokalizację, a czas przylotu jako nowy czas.

STAN CELOWY: Miasto docelowe. Czasami cel może być bardziej złożony, np. „przylot do miejsca docelowego lotem bez przesiadek”.

KOSZT DZIAŁANIA: połączenie kosztów pieniężnych, czasu oczekiwania, czasu lotu, procedur celnych i imigracyjnych, jakości miejsc, pory dnia, typu samolotu, punktów za częste loty i tak dalej.

Komercyjne systemy doradztwa turystycznego wykorzystują takie sformułowanie problemu, z wieloma dodatkowymi komplikacjami w obsłudze bizantyjskich struktur taryfowych linii lotniczych. Każdy doświadczony podróżnik wie jednak, że nie wszystkie podróże lotnicze przebiegają zgodnie z planem. Naprawdę dobry system powinien zawierać plany awaryjne – co się stanie, jeśli ten lot się opóźni i połączenie zostanie utracone?

Problemy z wycieczkami opisują zbiór lokalizacji, które należy odwiedzić, a nie jeden cel. Problem komiwojażera (TSP) to problem zwiedzania, w którym każde miasto na mapie musi zostać odwiedzone. Celem jest znalezienie wycieczki z kosztami (lub w wersji optymalizacyjnej znalezienie wycieczki z możliwie najniższym kosztem). Ogromną ilość wysiłku włożono w poprawę możliwości algorytmów TSP. Algorytmy można również rozszerzyć, aby obsługiwać floty pojazdów. Na przykład algorytm wyszukiwania i optymalizacji wyznaczania tras autobusów szkolnych w Bostonie zaoszczędził 5 milionów dolarów, ograniczył ruch uliczny i zanieczyszczenie powietrza oraz zaoszczędził czas kierowców i studentów (Bertsimas i in., 2019). Oprócz planowania podróży, algorytmy wyszukiwania były wykorzystywane do zadań takich jak planowanie ruchów automatycznych wiertarek do płytek drukowanych i maszyn magazynujących na halach produkcyjnych.

Problem z układem VLSI wymaga umieszczenia milionów komponentów i połączeń na chipie, aby zminimalizować obszar, zminimalizować opóźnienia obwodów, zminimalizować zbędne pojemności i zmaksymalizować wydajność produkcji. Problem z układem pojawia się po logicznej fazie projektowania i zwykle dzieli się na dwie części: układ komórek i routing kanałów. W układzie komórki prymitywne komponenty obwodu są pogrupowane w komórki, z których każda pełni pewną rozpoznaną funkcję. Każda komórka ma stały ślad (rozmiar i kształt) i wymaga określonej liczby połączeń z każdą z pozostałych komórek. Celem jest umieszczenie ogniw na chipie tak, aby nie zachodziły na siebie i aby było miejsce na umieszczenie przewodów łączących między ogniwami. Routing kanałów znajduje określoną trasę dla każdego przewodu przez szczeliny między komórkami. Te problemy wyszukiwania są niezwykle złożone, ale zdecydowanie warte rozwiązania.

Nawigacja robotem jest uogólnieniem opisanego wcześniej problemu wyszukiwania tras. Zamiast podążać odrębnymi ścieżkami (takimi jak drogi w Rumunii), robot może wędrować dookoła, w efekcie tworząc własne ścieżki. W przypadku okrągłego robota poruszającego się po płaskiej powierzchni przestrzeń jest zasadniczo dwuwymiarowa. Kiedy robot ma ręce i nogi, które również muszą być kontrolowane, przestrzeń wyszukiwania staje się wielowymiarowa — jeden wymiar dla każdego kąta stawu. Zaawansowane techniki są wymagane tylko po to, aby zasadniczo ciągła przestrzeń poszukiwań była skończona (patrz Rozdział 26). Oprócz złożoności problemu, prawdziwe roboty muszą również radzić sobie z błędami w odczytach czujników i sterowania silnikami, z częściową obserwowalnością oraz z innymi czynnikami, które mogą zmieniać środowisko.

Automatyczne sekwencjonowanie złożonych obiektów (takich jak silniki elektryczne) przez robota jest standardową praktyką przemysłową od lat 70. XX wieku. Algorytmy najpierw znajdują wykonalną sekwencję montażu, a następnie pracują nad optymalizacją procesu. Minimalizacja ilości ręcznej pracy ludzkiej na linii montażowej może przynieść znaczne oszczędności czasu i kosztów. W problemach montażowych celem jest znalezienie kolejności, w jakiej należy składać części jakiegoś obiektu. Jeśli zostanie wybrana niewłaściwa kolejność, nie będzie możliwości dodania części w dalszej kolejności bez cofnięcia części już wykonanej pracy. Sprawdzanie wykonalności działania w sekwencji jest trudnym problemem geometrycznym ściśle związanym z nawigacją robota. Tak więc generowanie czynności prawnych jest kosztowną częścią sekwencjonowania montażu. Każdy praktyczny algorytm musi unikać eksploracji całej przestrzeni stanów z wyjątkiem niewielkiej części. Jednym z ważnych problemów związanych z montażem jest projektowanie białek, którego celem jest znalezienie sekwencji aminokwasów, które sfałdują się w trójwymiarowe białko o odpowiednich właściwościach, aby wyleczyć niektóre choroby.

Problem świata siatki to dwuwymiarowa prostokątna tablica kwadratowych komórek, w której agenci mogą przechodzić z komórki do komórki. Zazwyczaj agent może przemieszczać się do dowolnej wolnej od przeszkód sąsiedniej komórki – poziomo lub pionowo, aw niektórych problemach po przekątnej. Komórki mogą zawierać obiekty, które agent może podnieść, popchnąć lub w inny sposób działać; ściana lub inna nieprzejezdna przeszkoda w komórce uniemożliwia agentowi przejście do tej komórki. Świat próżni z sekcji wcześniejszej można sformułować jako problem świata siatki w następujący sposób:

* STANY: Stan świata mówi, które obiekty znajdują się w jakich komórkach. W świecie próżni obiekty są agentem i wszelkim brudem. W prostej wersji dwukomórkowej agent może znajdować się w jednej z dwóch komórek, a każde połączenie może zawierać brud lub nie, więc występują stany 2∙2∙2 = 8 (patrz Rysunek).

Ogólnie rzecz biorąc, środowisko próżniowe z n komórkami ma  n∙2n stanów

* STAN POCZĄTKOWY: Dowolny stan może być wyznaczony jako stan początkowy.

* AKCJE: W świecie dwóch komórek zdefiniowaliśmy trzy akcje: ssanie, ruch w lewo i ruch w prawo. W dwuwymiarowym, wielokomórkowym świecie potrzebujemy więcej akcji ruchowych. Moglibyśmy dodać W górę i W dół, dając nam cztery bezwzględne akcje ruchu, lub moglibyśmy przełączyć się na akcje egocentryczne, zdefiniowane w odniesieniu do punktu widzenia agenta, na przykład: Do przodu, Do tyłu, Skręć w prawo i Skręć w lewo.

* MODEL PRZEJŚCIOWY: Ssanie usuwa wszelkie zabrudzenia z komórki agenta; Naprzód przesuwa agenta do przodu o jedną komórkę w kierunku, w którym jest zwrócony, chyba że uderzy w ścianę, w którym to przypadku akcja nie ma żadnego efektu. Wstecz przesuwa agenta w przeciwnym kierunku, podczas gdy skręty w prawo i skręty w lewo zmieniają kierunek, w którym jest zwrócony o 90^o

* STANY CELÓW: Stany, w których każda komórka jest czysta.

* KOSZT AKCJI: Każda akcja kosztuje 1.

Innym rodzajem świata gridowego jest łamigłówka sokoban, w której celem agenta jest zepchnięcie szeregu pudełek rozsianych po siatce do wyznaczonych miejsc przechowywania. Na komórkę może przypadać najwyżej jedno pudełko. Gdy agent przechodzi do komórki zawierającej pudełko, a po drugiej stronie pudełka znajduje się pusta komórka, zarówno pudełko, jak i agent poruszają się do przodu. Agent nie może wepchnąć pudełka do innego pudełka lub ściany. W świecie z n komórkami i b pudełkami bez przeszkód istnieją  n x n! / b!(n-b!) stany; na przykład na siatce  8 x 8 z tuzinem pudełek jest ponad 200 bilionów stanów. W układance z przesuwanymi płytkami wiele płytek (czasami nazywanych blokami lub kawałkami) jest ułożonych w siatkę z jednym lub więcej pustymi miejscami, tak aby niektóre płytki mogły wsunąć się w pustą przestrzeń. Jednym z wariantów jest łamigłówka Godziny szczytu, w której samochody i ciężarówki ślizgają się po siatce 6 x 6 , próbując uwolnić samochód z korka. Być może najbardziej znanym wariantem jest 8-puzzle (patrz Rysunek ), która składa się z siatki z ośmioma ponumerowanymi płytkami i jednym pustym polem oraz 15-puzle na siatce 4 x 4.

Celem jest osiągnięcie określonego stanu docelowego, takiego jak ten pokazany po prawej stronie rysunku. Standardowe sformułowanie 8 puzzli jest następujące:

* STANY: Opis stanu określa położenie każdej z płytek.

* STAN POCZĄTKOWY: Dowolny stan może być wyznaczony jako stan początkowy. Zauważ, że właściwość parzystości dzieli przestrzeń stanów – każdy cel można osiągnąć dokładnie z połowy możliwych stanów początkowych.

* AKCJE: Podczas gdy w świecie fizycznym jest to kafel, który się przesuwa, najprostszym sposobem opisania akcji jest myślenie o pustym miejscu poruszającym się w lewo, w prawo, w górę lub w dół. Jeśli półfabrykat znajduje się na krawędzi lub rogu, nie wszystkie działania będą miały zastosowanie.

* MODEL PRZEJŚCIOWY: Odwzorowuje stan i akcję na stan wynikowy; na przykład, jeśli zastosujemy Lewo do stanu początkowego na rysunku  , wynikowy stan ma zamienione 5 i puste pole.

* STAN CELOWY: Chociaż każdy stan może być celem, zazwyczaj określamy stan za pomocą liczb w kolejności

* KOSZT AKCJI: Każda akcja kosztuje 1.

Zauważ, że każde sformułowanie problemu zawiera abstrakcje. Obszary składające się z 8 zagadek są skupione na ich początkowych i końcowych stanach, ignorując pośrednie miejsca, w których kafelek się przesuwa. Wyodrębniliśmy działania, takie jak potrząsanie płytą, gdy płytki utkną, i wykluczyliśmy wyrywanie płytek nożem i ponowne ich odkładanie. Pozostaje nam opis zasad, unikając wszelkich szczegółów fizycznych manipulacji. Nasz ostateczny ustandaryzowany problem został opracowany przez Donalda Knutha (1964) i ilustruje, jak mogą powstawać nieskończone przestrzenie stanów. Knuth przypuszczał, że począwszy od liczby 4, ciąg operacji pierwiastka kwadratowego, podłogi i silni może osiągnąć dowolną liczbę całkowitą dodatnią. Na przykład możemy osiągnąć 5 z 4 w następujący sposób:

Definicja problemu jest prosta:

* STAN: Dodatnie liczby rzeczywiste.

* STAN POCZĄTKOWY: 4.

* DZIAŁANIA: Zastosuj pierwiastek kwadratowy, dolny lub silnię (silnia tylko dla liczb całkowitych).

* MODEL PRZEJŚCIOWY: Zgodnie z matematycznymi definicjami operacji.

* STAN DOCELOWY: Żądana dodatnia liczba całkowita.

* KOSZT AKCJI: Każda akcja kosztuje 1.

Przestrzeń stanów dla tego problemu jest nieskończona: dla dowolnej liczby całkowitej większej niż 2 operator silni zawsze da większą liczbę całkowitą. Problem jest interesujący, ponieważ bada bardzo duże liczby: najkrótsza droga do 5 prowadzi przez (4!)! = 620,448,401,733,239,439,360,000. Nieskończone przestrzenie stanów pojawiają się często w zadaniach związanych z generowaniem wyrażeń matematycznych, obwodów, dowodów, programów i innych obiektów definiowanych rekurencyjnie.

Podejście do rozwiązywania problemów zostało zastosowane w szerokiej gamie środowisk zadaniowych. Wymieniamy tutaj niektóre z najbardziej znanych, rozróżniając problemy standardowe i rzeczywiste. Standaryzowany problem ma na celu zilustrowanie lub przećwiczenie różnych metod rozwiązywania problemów. Może mieć zwięzły, dokładny opis, dlatego nadaje się jako punkt odniesienia dla badaczy do porównywania wydajności algorytmów. Problem w świecie rzeczywistym, taki jak nawigacja robotem, to taki, którego rozwiązania faktycznie wykorzystują ludzie i którego sformułowanie jest specyficzne, a nie znormalizowane, ponieważ na przykład każdy robot ma inne czujniki, które generują różne dane.

Nasze sformułowanie problemu dotarcia do Bukaresztu jest modelem – abstrakcyjnym opisem matematycznym — a nie rzeczywistością. Porównaj prosty opis stanu atomowego Arad do prawdziwej podróży przez kraj, gdzie stan świata obejmuje tak wiele rzeczy: towarzyszy podróży, aktualny program radiowy, sceneria za oknem, bliskość funkcjonariuszy organów ścigania, odległość do następnego postoju, stan drogi, pogoda, ruch uliczny i tak dalej. Wszystkie te rozważania zostały pominięte w naszym modelu, ponieważ nie mają związku z problemem znalezienia drogi do Bukaresztu. Proces usuwania szczegółów z reprezentacji nazywamy abstrakcją. Dobre sformułowanie problemu ma odpowiedni poziom szczegółowości. Gdyby działania były na poziomie „przesuń prawą nogę do przodu o centymetr” lub „obróć kierownicę o jeden stopień w lewo”, agent prawdopodobnie nigdy nie wydostałby się z parkingu, nie mówiąc już o Bukareszcie.

Czy możemy dokładniej określić odpowiedni poziom abstrakcji? Pomyśl o abstrakcyjnych stanach i działaniach, które wybraliśmy jako odpowiadających dużym zbiorom szczegółowych stanów świata i szczegółowych sekwencji działań. Rozważmy teraz rozwiązanie abstrakcyjnego problemu: na przykład drogę z Aradu do Sibiu, Rimnicu Vilcea, Pitesti, Bukaresztu. To abstrakcyjne rozwiązanie odpowiada dużej liczbie bardziej szczegółowych ścieżek. Na przykład moglibyśmy jechać z włączonym radiem między Sibiu a Rimnicu Vilcea, a potem je wyłączyć na resztę podróży. Abstrakcja jest słuszna, jeśli możemy przekształcić dowolne abstrakcyjne rozwiązanie w rozwiązanie w bardziej szczegółowym świecie; warunkiem wystarczającym jest to, że dla każdego szczegółowego stanu „w Arad” istnieje szczegółowa ścieżka do jakiegoś stanu „w Sybinie” i tak dalej. Abstrakcja jest przydatna, jeśli wykonanie każdego z działań w rozwiązaniu jest łatwiejsze niż oryginalnego problemu; w naszym przypadku akcję „jazda z Arad do Sibiu” można przeprowadzić bez dalszych poszukiwań lub planowania przez kierowcę o przeciętnych umiejętnościach. Wybór dobrej abstrakcji polega zatem na usunięciu jak największej ilości szczegółów przy jednoczesnym zachowaniu ważności i zapewnieniu, że abstrakcyjne działania są łatwe do wykonania. Gdyby nie umiejętność konstruowania użytecznych abstrakcji, inteligentni agenci zostaliby całkowicie zasypani przez świat rzeczywisty.

Problem wyszukiwania można formalnie zdefiniować w następujący sposób:

* Zbiór możliwych stanów, w których może znajdować się środowisko. Nazywamy to przestrzenią stanów.

* Stan początkowy, w którym uruchamia się agent. Na przykład: Arad.

* Zestaw co najmniej jednego stanu celu. Czasami istnieje jeden stan docelowy (np. Bukareszt), czasami istnieje niewielki zbiór alternatywnych stanów docelowych, a czasami cel jest określony przez właściwość, która odnosi się do wielu stanów (potencjalnie nieskończonej liczby). Na przykład w świecie odkurzaczy celem może być brak brudu w dowolnym miejscu, niezależnie od innych faktów dotyczących stanu. Możemy wyjaśnić wszystkie trzy z tych możliwości, określając metodę IS-GOAL dla problemu. W tym rozdziale będziemy czasami mówić „cel” dla uproszczenia, ale to, co mówimy, odnosi się również do „dowolnego z możliwych stanów celu”.

* Akcje dostępne dla agenta. s ACTIONS(s) danego stanu zwraca skończony zbiór akcji, które mogą być wykonane w. Mówimy, że każda z tych akcji ma zastosowanie w s. Przykład:

ACTIONS(Arad) = {ToSibiu, ToTimisoara, ToZerind}.

* Model przejścia, który opisuje, co robi każda akcja. RESULT(s,a) zwraca stan wynikający z wykonania akcji w stanie s .Na przykład

RESULT(Arad; ToZerind) = Zerind.

* Funkcja kosztu akcji, oznaczana przez ACTION-COST(s,a,s’) kiedy programujemy lub c(s,a,s’) kiedy wykonujemy matematykę, która daje liczbowy koszt zastosowania akcji w stanie osiągnąć stan s”. Agent rozwiązujący problemy powinien używać funkcji kosztu, która odzwierciedla jego własną miarę wydajności; na przykład, w przypadku agentów wyszukujących trasy, kosztem działania może być długość w milach (jak widać na rysunku 3.1 ) lub może to być czas potrzebny na ukończenie działania. Sekwencja działań tworzy ścieżkę, a rozwiązanie jest ścieżką od stanu początkowego do stanu docelowego. Zakładamy, że koszty działania są addytywne; oznacza to, że całkowity koszt ścieżki jest sumą kosztów poszczególnych działań. Optymalne rozwiązanie ma najniższy koszt ścieżki spośród wszystkich rozwiązań. W tym rozdziale zakładamy, że wszystkie koszty działań będą dodatnie, aby uniknąć pewnych komplikacji. Przestrzeń stanów można przedstawić jako graf, w którym wierzchołkami są stany, a skierowane między nimi krawędzie są działaniami. Mapa Rumunii pokazana na rysunku powyżej jest takim wykresem, gdzie każda droga wskazuje dwa działania, po jednym w każdym kierunku.