Obliczanie liczb Fibonacciego jest tradycyjnym przykładem przy nauczaniu rekurencji. Tutaj użyjemy go do porównania wydajności dwóch algorytmów, jednego rekurencyjnego i jednego sekwencyjnego. Jeśli ich nie znasz, liczby Fibonacciego są definiowane rekurencyjnie w sekwencji, w której następna jest sumą dwóch poprzednich, a dwie pierwsze liczby to jedynki (nasze przypadki bazowe). Rzeczywista sekwencja to 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 i tak dalej. Nazywa się to ciągiem Fibonacciego i wykazuje interesujące właściwości, takie jak związek ze złotym podziałem, na który zdecydowanie powinieneś sprawdzić, jeśli nie wiesz, co to jest. Nasza funkcja fivbonaci_recursive() przyjmuje pozycję liczby Fibonacciego, którą chcemy obliczyć jako n, ograniczoną do liczb całkowitych większych lub równych jeden. Jeśli jest to przypadek podstawowy, to znaczy, jeśli jest poniżej 1, po prostu go zwrócimy (nie, że jeśli obliczamy liczbę Fibonacciego na drugiej pozycji, nasza operacja n-2 wyniesie zero, co nie jest prawidłową pozycją, dlatego musimy użyć <= zamiast ==). W przeciwnym razie zwrócimy sumę wywołań rekurencyjnych do dwóch poprzednich za pomocą fibonacci_recursive(n-1) i fibonacci_recursive(n-2), jak pokazano w poniższym fragmencie kodu:
fibonacci_recursive <- function(n) {
if(n <= 1) {return(n) }
return(fibonacci_recursive(n-1) + fibonacci_recursive(n-2)
Jak widać na poniższym fragmencie kodu, nasza funkcja działa zgodnie z oczekiwaniami. Co się jednak dzieje, gdy chcemy pobrać 35 lub 40 liczbę Fibonacciego? Jak możesz doświadczyć podczas uruchamiania tego kodu, im dalej liczba Fibonacciego jest od przypadków podstawowych, tym więcej czasu zajmie, a gdzieś w okolicach 30. pozycji zaczyna być zauważalnie wolniejsza. Jeśli spróbujesz obliczyć setną liczbę Fibonacciego, będziesz czekać długo, zanim otrzymasz wynik:
fibonacci_recursive(1)
#> [1] 1
fibonacci_recursive(2)
#> [1] 1
fibonacci_recursive(3)
#> [1] 2
fibonacci_recursive(4)
#> [1] 3
fibonacci_recursive(5)
#> [1] 5
fibonacci_recursive(35)
#> [1] 9227465
Dlaczego to się dzieje? Odpowiedź brzmi, że ten algorytm wykonuje dużo niepotrzebnej pracy, co czyni go złym algorytmem. Aby zrozumieć, dlaczego, przejdźmy mentalnie przez wykonanie algorytmu dla trzeciej i czwartej liczby Fibonacciego i utwórzmy odpowiednie drzewa wykonania, jak pokazano na poniższym diagramie:
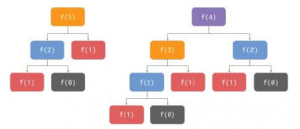
Na poprzednim diagramie f(n) jest skrótem od fibonacci_recursive(n) , dzięki czemu możemy zmieścić wszystkie obiekty w nim, a kolory są używane do pokazania, które wywołania funkcji są powtarzane. Jak widać, podczas wykonywania fibonacci_recursive(3) , fibonacci_recursive(1) wywołanie jest wykonywane dwukrotnie. Podczas wykonywania fibonacci_recursive(4) to samo wywołanie jest wykonywane trzy razy. Ile razy będzie to wykonywane za fibonacci_recursive(5) i fibonacci_recursive(6)? To ćwiczenie dla ciebie, czytelniku, a jak się przekonasz, liczba ta rośnie wykładniczo. Aby być technicznie precyzyjnym, złożoność czasowa algorytmu wynosi O(2n), co jest tak złe, jak tylko można. Ponadto większość obliczeń jest całkowicie niepotrzebna, ponieważ są one powtarzane. Algorytm jest poprawny, ale jego wydajność jest jedną z gorszych. Jak wspomnieliśmy wcześniej, nawet jeśli zapewnisz najbardziej wydajną implementację tego algorytmu, będzie to znacznie wolniejsze niż bardzo nieefektywna implementacja bardziej wydajnego. Jeśli zaprojektujemy poprawny algorytm, który pozwoli uniknąć wykonywania wszystkich niepotrzebnych obliczeń, możemy to zrobić mają znacznie szybszy program i właśnie to robi następujący algorytm. Zamiast tworzyć drzewo rekurencyjnych wywołań, po prostu obliczymy liczby Fibonacciego w kolejności aż do tej, o którą jesteśmy proszeni. Po prostu dodamy poprzednie dwie liczby i zapiszemy wynik w tablicy, która będzie zawierała liczby całkowite. Określamy dwa przypadki podstawowe i kontynuujemy obliczenia, jak pokazano w poniższym fragmencie kodu:
fibanacci_sequential <- funtion(n) {
if (n <= 2) { return(1)
f <- integer(n)
f[1] <- 1
f[2] <- 1
for (i in 3:n) {
f[i] <- f[i-2] + f[i-1]
}
return(f[n])
Jak widać, każda liczba jest obliczana tylko raz, co jest najbardziej wydajnym algorytmem, jaki możemy zaprojektować dla tego problemu. Pozwala to uniknąć całego narzutu związanego z algorytmem rekurencyjnym i pozostawia nam liniową złożoność czasową O (n). Nawet jeśli kodujemy ten algorytm bez dbania o optymalizację wydajności, jego czas wykonania będzie szybszy o wiele rzędów wielkości. Za pomocą tego algorytmu możemy w rzeczywistości obliczyć 1476 liczbę Fibonacciego, która jest największą, na jaką pozwala architektura wewnętrzna R. Jeśli spróbujemy obliczyć 1477. liczbę Fibonacciego, otrzymamy nieskończoność (Inf) jako odpowiedź ze względu na mechanizmy używane przez R do przechowywania liczb całkowitych, co jest tematem, którym nie będziemy się zajmować. Co więcej, obliczenia dla 1476 liczby Fibonacciego są prawie natychmiastowe, co pokazuje, jak ważne jest wybranie dobrego algorytmu, zanim zacznie się go optymalizować:
fibonacci_sequemtial(1476)
# [1] 1.306989e + 308
fibonacci_sequemtial(1477)
#[1] Inf
Na koniec zauważ, że osiągnęliśmy wzrost szybkości kosztem wykorzystania większej ilości pamięci. Algorytm rekurencyjny odrzucał każdą liczbę Fibonacciego po jej obliczeniu, podczas gdy algorytm sekwencyjny przechowuje każdą w pamięci. W przypadku tego konkretnego problemu wydaje się to być dobrym kompromisem. Kompromis między czasem i przestrzenią jest powszechny w optymalizacji wydajności. Teraz, gdy zobaczyliśmy, jak ważny może być wybór algorytmu, w dalszej części rozdziału będziemy pracować z jednym algorytmem i skupimy się na optymalizacji jego implementacji. Pozostaje jednak kwestia, że wybór wydajnego algorytmu jest ważniejszy niż efektywne jego wdrożenie.