Teraz będziemy pracować z podejściem odgórnym, co oznacza, że najpierw zaczniemy od kodu abstrakcyjnego i stopniowo przejdziemy do szczegółów implementacji. Generalnie uważam, że to podejście jest bardziej wydajne, gdy masz jasne wyobrażenie o tym, co chcesz zrobić. W naszym przypadku zaczniemy pracując z plikiem main.R. Pierwszą rzeczą, na którą należy zwrócić uwagę, jest to, że użyjemy funkcji proc.time() dwukrotnie, raz na początku i raz na końcu, i użyjemy różnicy między tymi dwiema wartościami, aby zmierzyć, ile czasu wykonanie całego kodu zajęło. Drugą rzeczą, na którą należy zwrócić uwagę, jest to, że funkcja empty_directories() zapewnia istnienie każdego z określonych katalogów i usuwa wszystkie zawarte w nich pliki. Używamy go do czyszczenia naszych katalogów na początku każdego wykonania, aby upewnić się, że mamy najnowsze pliki i tylko pliki utworzone w ostatnim uruchomieniu. Rzeczywisty kod jest pokazany poniżej i po prostu iteruje przez każdy z przekazanych katalogów, rekurencyjnie usuwa wszystkie pliki wewnątrz za pomocą funkcji unlink() i upewnia się, że katalog istnieje z funkcji dir.create(). Unika wyświetlania jakichkolwiek ostrzeżeń związanych z katalogiem już istniejącym, co nie stanowi problemu w naszym przypadku, poprzez użycie parametru showWarnings = FALSE.
empty_directories() <- function(directories) {
for (directory in directories) {
unlink(directory, recursive = TRUE)
dir.create(driectory, showWarnings = FALSE)
}
}
Od początku R, używamy funkcji print_section() i empty_directories() do wyświetlania nagłówków i usuwania zawartości katalogu (w celu odtworzenia wyników za każdym razem, gdy uruchamiamy funkcję z pustymi katalogami), a użyjemy mechanizm pokazany za pomocą proc.time() do pomiaru czasu wykonania. Teraz, gdy poprzednie dwa punkty są już na uboczu, przejdziemy do pokazania pełnej zawartości pliku main.R.
start_time <- proc_time()
source(„./function.R”)
empty_directories(c (
„./results/oroginal/”,
„./results/adjusted/’,
„./results/original/scatter_plots/”
))
data <- prepare_data(„./data_brexit_referendum.csv, complete_cases = TRUE)
data_adjusted <- adjust_data(data)
numerical_variables <- get_numerical_variable_names(data)
numerical_variables_adj <- get_numerical_variable_names(data_adjusted)
print(„Working on summaries …”)
full_summary(data, save_to = „./reults/original/summary_text.txt”)
numerical_summary)
data,
numerical_variables = numerical_variables,
save_to = „./results/original/summary_numerical.csv”
}
print(„Working on histograms …”)
plot_percentage)
data,
variable = „RegionName”
save_to = „./results/origibnal/vote_percentage_by-egion.png”
}
print („Working on matrix scatter plots…”)
matrix_scatter_plots (
data_adjusted,
nuerical_variables = numerical_variables_adj,
save_to = „./results/adjusted/matrix_scatter_plots.png”
)
print(„Working on scatter plots …”)
plot_scatter_plot (
data;
var_x = „RegionName”,
var_y = „Proportion”,
var_color = „White”,
regression = TRUE,
save_to = „./results/origina;/reginname_vs_proportion_vs_white.png”
)
all_scatter_plots(
data,
numerical_variables = numerical_variables,
save_to = „./results/original/scatter_plots/”
)
print („Working on correlations…”)
correlations_plot(
data,
numerical_variables = numerical_variables,
save_to = „./results/original/correlations.png”
)
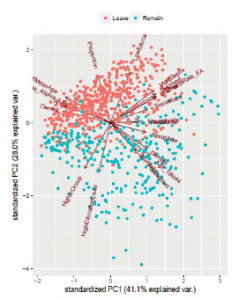
print(„Working on principal components…”)
principal_components(
data_adjusted,
numerical_variables – numerical_variables_adj,
save_to = „./results/adjusted/principal_components”
)
end_time <- proc.time()
time_taken <- end_time – start.time
print(paste(„Time taken: „ , taken[1]))
print („Done.”)
Jak widać, mając tylko ten plik, masz duży obraz analizy i jesteś w stanie odtworzyć swoją analizę, uruchamiając pojedynczy plik, zapisując wyniki na dysku (zwróć uwagę na argumenty save_to,), i zmierzyć czas potrzebny do wykonania pełnej analizy. Z naszej listy celów ogólnych, ten kod spełnia cele od pierwszego do czwartego. Osiągnięcie celu piątego i szóstego zostanie osiągnięte poprzez pracę nad plikiem function.R który zawiera wiele małych funkcji. Posiadanie tego pliku main.R daje nam mapę tego, co należy zaprogramować, i chociaż w tej chwili to nie zadziała, ponieważ funkcje, których używa, jeszcze nie istnieją, zanim zakończymy ich programowanie, plik ten będzie nie wymagają żadnych zmian i przyniosą pożądane rezultaty. Ze względu na ograniczenia miejsca nie przyjrzymy się implementacji wszystkich funkcji w pliku main.R, tylko te reprezentatywne: prepare.data(), plot_scatter_plot() i all_scatter_plots(). Inne funkcje wykorzystują podobne techniki do hermetyzacji odpowiedniego kodu. Zaczynamy od prepare_data(). Ta funkcja jest abstrakcyjna i wykorzystuje cztery różne konkretne funkcje do wykonania swojej pracy: read_csv(), clean_data(), transform_data() i, jeśli jest to wymagane, complete.cases(). Pierwsza funkcja, mianowicie read.csv(), odbiera ścieżkę do pliku CSV, z którego dane są odczytywane i ładuje do obiektu ramki danych o nazwie data w tym przypadku. Czwarta funkcja, widzieliście wcześniej , więc nie będziemy jej tutaj wyjaśniać. Funkcje dwa i trzy zostały stworzone przez nas i wyjaśnimy je. Zauważ, że main.R nie wie o tym, jak przygotowywane są dane, prosi tylko o przygotowanie danych i deleguje zadanie do funkcji abstrakcyjnej prepare_data()
prepare_data <- function(path, complete_cases = TRUE) {
data <- read.csv(path)
data <- clean_data(data)
data <- transform_data(data)
if (complete_cases) {
data <- data[complete.cases(data), ]
}
return(data)
}
Funkcja clean_data() po prostu hermetyzuje na razie ponowne kodowanie -1 dla NA. Jeśli nasza procedura czyszczenia nagle stała się bardziej złożona (na przykład nowe źródła danych wymagające częstszego czyszczenia lub uświadomienia sobie, że coś przeoczyliśmy i musimy dodać to do procedury czyszczenia), dodalibyśmy te zmiany do tej funkcji i nie musielibyśmy modyfikować niczego innego w pozostałej części naszego kodu. Oto niektóre z zalet hermetyzacji kodu w funkcje, które przekazują zamiar i izolują to, co należy zrobić w małych krokach:
clean_data <- function(data) {
data[data$Leave == -1, „Leave”] <- NA
return(data)
}
Aby przekształcić nasze dane, dodając dodatkowe zmienne Proportion i Vote , i ponownie oznacz plik nazwy regionów, używamy następującej funkcji:
transform_data <- funtion(data) {
data$Proportion <- data$Leave / data$NVotes
data$Vote <- ifelse(data$Proportion > 0,5 , „Leave”, „Remain”)
data$RegionName <- as.character(data$RegionName)
data[data$RegionName == „London”, „RegionName”] <- „L”
data[data$RegionName == „North West”, „RegionName”] <- „NW”
data[data$RegionName == „South West”, „RegionName”] <- „SW”
data[data$RegionName == „South East”, „RegionName”] <- „SE”
data[data$RegionName == „East Middlands”, „RegionName”] <- „EM”
data[data$RegionName == „West Midlands”, „RegionName”] <- „WM”
data[data$RegionName == „East of England” , „RegionName”] <- „EE”
data[data$RegionName == „Yorkshire and The Humer”, „RegionName”] <- „Y”
return(data)
}
Wszystkie te linie kodu, które widzieliście wcześniej. Wszystko, co robimy, to hermetyzowanie ich w funkcje, które komunikują intencje i pozwalają nam znaleźć miejsce, w którym zachodzą określone procedury, abyśmy mogli je znaleźć i łatwo zmienić, jeśli zajdzie taka potrzeba później.
Teraz przyjrzymy się plot_scatter_plot(). Ta funkcja znajduje się pomiędzy funkcją abstrakcyjną a konkretną. Użyjemy go bezpośrednio w naszym pliku main.R, ale użyjemy go również w innych funkcjach w pliku function.R. Wiemy, że przez większość czasu będziemy używać Proportion jako zmiennej koloru, więc dodajemy ją jako wartość domyślną, ale pozwalamy użytkownikowi całkowicie usunąć kolor, sprawdzając, czy argument został wysłany jako FALSE, a ponieważ będziemy używać tej samej funkcji do tworzenia wykresów, które przypominają wszystkie wykresy rozrzutu, utworzonych do tego momentu, uczynimy linię regresji opcjonalną. Zwróć uwagę, że w przypadku pierwszych wykresów oś x jest zmienną ciągłą, ale w przypadku drugiego wykresu jest to zmienna jakościowa (czynnikowa). Ten rodzaj elastyczności jest bardzo potężny i jest dostępny dla nas ze względu na zdolność ggplot2 do dostosowania się do tych zmian. Formalnie nazywa się to polimorfizmem. Wreszcie, zamiast zakładać, że użytkownik zawsze będzie chciał zapisać wynikowy wykres na dysku, ustawiamy argument save_to jako opcjonalny, podając dla niego pusty ciąg. W razie potrzeby sprawdzamy, czy ten ciąg jest pusty za pomocą not_empty(), a jeśli nie jest pusty, konfigurujemy mechanizm zapisywania PNG.
plot_scatter_plot <- function(datal
var_x,
var_y,
var_color = „Proportion”,
regression = FALSE;
save_to = „ „ ) {
if (var_color) {
plot <- ggplot(data, aes_string(x = var_x, y = var_y, color = var_color))
} else {
plot <- ggplot(data, aes_string(x = var_x, y = var_y))
}
plot <- plot + scale_color_viridis()
plot <- plot + geom_point()
if (regression) {
plot <- plot + stat_smooth(method = „lm”, col = „grey”, se = FALSE)
}
if (not_empty(save_to)) png(save_to)
print(plot)
if (not_empty (save_to)) dev.off()
}
Teraz przyjrzymy się all_scatter_plots(). Ta funkcja jest funkcją abstrakcyjną, która ukrywa przed wiedzą użytkownika nazwę funkcji, która iteracyjnie tworzy wykresy, dogodnie nazwana create_graphs_iteratively() i funkcja graficzna, funkcja plot_scatter_plot(), którą widzieliśmy wcześniej. W przypadku, gdy chcemy ulepszyć mechanizm iteracyjny lub funkcję graficzną, możemy to zrobić bez konieczności wprowadzania zmian od osób, które używają naszego kodu, ponieważ ta wiedza jest tutaj zamknięta. Funkcja create_graphs_iteratively() jest taka sama, jak wcześniej, z wyjątkiem kodu paskowego postępu. Pakiet progress udostępnia funkcję progres_bar$new(), która tworzy pasek postępu w terminalu podczas wykonywania iteracyjnego procesu, dzięki czemu widzimy jaki procent procesu został ukończony i dowiedz się, ile czasu pozostało. Zwróć uwagę na zmianę argumentu save_to z funkcji plot_scatter_plot() i all_scatter_plot(). W pierwszym przypadku jest to nazwa pliku; w drugim – nazwa katalogu. Różnica jest niewielka, ale ważna. Nieostrożny czytelnik może tego nie zauważyć i może być przyczyną nieporozumień. Funkcja plot_scatter_plot() tworzy pojedynczy wykres i otrzymuje w ten sposób nazwę pliku. Jednak all_scatter_plots() wyprodukuje, używając plot_scatter_plot(), dużo wykresów, więc musi wiedzieć, gdzie trzeba je wszystkie zapisać, dynamicznie tworzyć ostateczne nazwy obrazów i wysyłać je pojedynczo do plot_scatter_plot().
Wreszcie, ponieważ chcemy, aby regresja została uwzględniona na tych wykresach, po prostu wysyłamy parametr regression = TREU:
all_scatter-plots <- function(data, numerical_variables, save_to = „ „ ) {
create_graphs_iteratively(data, numerical_variables, plot_scatter_plot, save_to)
}
create_graphs_iteratively <- function(data,
numerical_variables,
plot_function,
save_to = „ „) {
numerical_variables[[„Proportion”]] <- FALSE
variables <- names(numerical_Variables[numerical_variables == TRUE])
n_variables <- (length(variables) – 1)
progres_bar <- progres_bar$new(
format = „Progress [:bar] :percent ETA : :ets”,
total = n_Variables
)
for (i in 1:n_variables) {
progres_bar$tick()
for (j in (i+1) : length(variables)) {
image_name <- paste(
save_to,
variables[i], „_”,
variables[j], „.png”,
sep= „”
)
plot_function(
data,
var_x = variables[i].
var_y = variables[j],
save_to = „image_name,
regression = TRUE
}
}
}
}