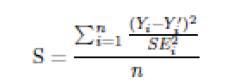Miesiąc: listopad 2020

Teraz, gdy widzieliśmy, jak tworzyć wyniki, które reprezentują, jak dobra lub zła jest moc predykcyjna modelu, możesz zacząć określać wiele modeli ręcznie, zmieniając kombinacje zmiennych wysyłanych do funkcji lm(), obliczając wartości każdego modelu. wyniki, a następnie wybierz te z największą mocą predykcyjną. Może to zająć dużo czasu i możesz chcieć przekazać to komuś innemu, ponieważ jest to żmudna praca. Jednak nie bój się. Jest lepszy sposób! Komputery są dobre w powtarzalnych i żmudnych zadaniach, a teraz zobaczymy, jak powiedzieć komputerowi, aby znalazł dla nas najlepszy model przy odrobinie programowania. Poniższe sekcje zwiększą poziom programowania, ale nie martw się, wyjaśnimy szczegółowo kod, aby upewnić się, że wszystko jest zrozumiałe. Jeśli w jakimkolwiek momencie poczujesz się zdezorientowany, zawsze możesz skopiować i wkleić małe fragmenty kodu do terminala R i zobaczyć, co każdy z nich robi z osobna, aby stopniowo uzyskać sens całej sprawy

Teraz, gdy sprawdziliśmy założenia naszego modelu, przechodzimy do pomiaru jego mocy predykcyjnej. Aby zmierzyć naszą dokładność predykcyjną, użyjemy dwóch metod, jednej dla danych liczbowych (Proportion), a drugiej dla danych jakościowych (Vote). Wiemy, że zmienna Vote jest transformacją ze zmiennej Proprotion, co oznacza, że ​​mierzymy te same informacje na dwa różne sposoby. Jednak zarówno dane liczbowe, jak i jakościowe są często spotykane w analizie danych, dlatego chcieliśmy tutaj pokazać oba podejścia. Obie funkcje, score_proportion() (numeryczna) i score_votes () (kategoryczna) otrzymujemy dane, których używamy do testowania i prognozy dla każdej obserwacji w danych testowych, które pochodzą z modelu, który zbudowaliśmy w poprzednich sekcjach.

W przypadku liczbowym score_proprotios() oblicza wynik przy użyciu następującego wyrażenia:

Tutaj Y_i to rzeczywista wartość zmiennej odpowiedzi dla i-tej obserwacji w danych testowych, Y’_i to nasza prognoza dla tej samej obserwacji, SE to błąd standardowy naszej prognozy, a n to liczba obserwacji w testowaniu dane. To równanie ustala, że ​​wynik, który chcemy zminimalizować, jest średnią studentyzowanych reszt. Jak zapewne wiesz, reszty studenckie to reszty podzielone przez miarę błędów standardowych. Ta formuła daje nam średnią miarę tego, jak blisko jesteśmy do prawidłowego przewidzenia wartości obserwacji w stosunku do wariancji obserwowanej dla tego zakresu danych. Jeśli mamy wysoki stopień wariancji (powodujący błędy o wysokim standardzie), nie chcemy być zbyt rygorystyczni w przewidywaniu, ale jeśli znajdujemy się w obszarze o niskiej wariancji, chcemy mieć pewność, że nasze przewidywania są bardzo dokładne:

score_proprotios <- funtio(data_test, predictios){

# se := stadad errors

se <- predictios$se.fit

real <- data_test$Proprotion

predicted <- predictions$fit

retur(sum((real – predicted)^2 / se^2) . nrow(datat))

}

W przypadku kategorycznym score_votes() oblicza wynik, po prostu licząc, ile razy nasze przewidywania wskazywały na właściwą kategorię, którą chcemy zmaksymalizować. Robimy to, używając najpierw tego samego mechanizmu klasyfikacji (jeśli przewidywane Proprotion jest większe niż 0,5, to klasyfikujemy go jako glos „Leave” i odwrotnie) i porównujemy wartości kategoryczne. Wiemy, że suma wektora boolowskiego będzie równa liczbie TRUE wartości i właśnie tego używamy w wyrażeniu sum(real == predictes:

score_votes <- function (data_test, preditions) {

real <- datta_test$Vote

predicted <- ifelse(predictions$fit > 0.5 , „Leave”, „Remain”)

return(sum(real == predicted))

}

Aby przetestować wyniki naszego modelu, wykonujemy następujące czynności:

predictios <- predict(fit, data_test, se.fit = TRUE)

score_proportions(data_test, predictions)

#> [1] 10,66

score_votes(data_test, predictions)

#> [1] 216

nrow(data_test)

#> [1] 241

W przypadku funkcji score_votes() sama miara mówi nam, jak dobrze sobie radzimy z naszymi przewidywaniami, ponieważ możemy wziąć liczbę poprawnych przewidywań (wynik wywołania funkcji , czyli 216) i podziel go przez liczbę obserwacji (wierszy) w obiekcie data_test (czyli 241). Daje nam to precyzję 89%. Oznacza to, że gdybyśmy otrzymali dane od regresorów, ale nie wiemy, jak faktycznie głosował podopieczny, w 89% przypadków przedstawilibyśmy prognozę, czy chcą odejść, czy pozostać na UE, co byłoby poprawne. To całkiem nieźle, jeśli o mnie chodzi. W przypadku funkcji score_proportions(), ponieważ używamy bardziej abstrakcyjnej miary, aby wiedzieć, jak dobrze sobie radzimy, chcielibyśmy aby porównać to z wynikami innych modeli i uzyskać względne poczucie mocy predykcyjnej modelu, i właśnie to zrobimy w następnych sekcjach.

Aby sprawdzić, czy nie ma kolinearności, możemy użyć wielu różnych technik. Na przykład dla osób zaznajomionych z algebrą liniową numer warunku jest miarą osobliwości macierzy, gdzie osobliwość oznaczałaby doskonałą współliniowość między zmiennymi towarzyszącymi. Ta liczba może stanowić miarę tej kolinearności. Inną techniką jest użycie współczynnika inflacji wariancji, który jest bardziej formalną techniką, która zapewnia miarę wzrostu wariancji regresji z powodu kolinearności. Innym i bardziej powszechnym sposobem sprawdzenia tego są proste korelacje. Czy są jakieś zmienne silnie skorelowane między sobą w tym sensie, że może istnieć między nimi bezpośredni związek? Jeśli tak, to możemy mieć problem z współliniowością. Poniższy kod pokazuje, jak działają korelacje w języku R:

library(corrplot)

corrplot(corr = cor(data[, numerical_variables]), tl.col = „black”, tl.cex = 0.6)

Jak widać, silne korelacje (dodatnie lub ujemne) występują wewnątrz grup, a nie między grupami, co oznacza, że ​​zmienne, które mierzą to samo na różne sposoby, wydają się być wysoce skorelowane, podczas gdy zmienne, które mierzą różne rzeczy, nie wydają się być wysoce skorelowane.

Na przykład Age_18to44  i Age_45plus to zmienne mierzące wiek i spodziewamy się, że będą miały negatywną relację, ponieważ im wyższy odsetek młodych ludzi na oddziale z konieczności odsetek osób starszych jest niższy. Ta sama zależność jest widoczna w grupie mieszkań (Owned, OwedOutright, SocialRent i PrivateRent ), grupa zatrudnionych (Unemp, UnempRate_EA i HigherOccup), grupa potrzebująca (Deprived i MultiDepriv), grupa etniczna (White i NonWhite), grupa zamieszkania (Residet i Housholds) oraz grupę edukacyjną (LowEducationLevel i HighEducationLevel). Jeśli wybierzesz zmienne należące do różnych grup, liczba silnych korelacji jest znacznie niższa, ale istnieje. Na przykład HigherOccup jest silnie skorelowane z HighEducatioLevel i LowEducatioLevel, pozytywnie i odpowiednio negatywnie. Wydaje się również, że zmienne w grupie mieszkaniowej są skorelowane ze zmiennymi w grupie wiekowej. Tego typu relacje są oczekiwane i naturalne, ponieważ osoby z wyższym wykształceniem będą miały zapewne lepszą pracę, a młodych ludzi prawdopodobnie jeszcze nie stać na mieszkanie, więc wynajmują. Jako analitycy możemy założyć, że zmienne te w rzeczywistości mierzą różne aspekty społeczeństwa i kontynuować naszą analizę. Jednak są to nadal rzeczy, o których warto pamiętać podczas interpretacji wyników. Możemy również chcieć uwzględnić tylko jedną zmienną w każdej grupie, aby uniknąć kolinearności między grupami, ale unikniemy tych zawiłości i będziemy kontynuować nasza analiza na razie. Regresja liniowa jest jednym z tych typów modeli, które wymagają od analityka przyjęcia lub odrzucenia kryteriów. W naszym konkretnym przypadku wydaje się, że założenia naszego modelu są wystarczająco słuszne i możemy go bezpiecznie wykorzystać do dostarczenia wiarygodnych prognoz, tak jak to zrobimy w następnych sekcjach

Sprawdzimy normalność za pomocą dwóch różnych technik, aby zilustrować użycie techniki znanej jako wzorzec strategii, która jest częścią zestawu wzorców z programowania obiektowego. Na razie możesz myśleć o schemacie strategii jako o technice, która ponownie wykorzysta kod, który w przeciwnym razie zostałby zduplikowany i po prostu zmienia sposób wykonywania rzeczy zwanych strategią. W poniższym kodzie widać, że tworzymy funkcję o nazwie save_png(), która zawiera kod, który zostałby zduplikowany (zapisywanie plików PNG) i nie musi być. Będziemy mieć dwie strategie, w postaci funkcji, sprawdzania normalności danych – histogramy i wykresy kwantyl-kwantyl. Zostaną one przesłane za pomocą argumentu o dogodnej nazwie function_to_create_images. Jak widać, ten kod otrzymuje pewne dane, zmienną, która zostanie użyta dla wykresu, nazwę pliku obrazu oraz funkcję, która zostanie użyta do utworzenia wykresów. Ten ostatni parametr, funkcja, nie powinien być nieznany czytelnikowi, że możemy wysyłać funkcje jako argumenty i używać ich tak, jak robimy w tym kodzie wywołując je poprzez ich nową nazwę wewnątrz funkcji, function_to_create_images() w tym przypadku:

save_png <- function(data,variable, save_to, function_to_create_image){

if (not_empty(save_to)) png(save_to)

function_to_create_image(data, variable)

if (not_empty(save_to)) dev.off()

}

Teraz pokażemy kod, który będzie używał tej funkcji save_png() i hermetyzujemy wiedzę o funkcji używanej w każdym przypadku. W przypadku histogramów funkcja histohram() pokazana w poniższym kodzie po prostu opakowuje funkcję hist() używaną do tworzenia wykresu ze wspólnym interfejsem, który będzie również używany przez inne strategie (w tym przypadku funkcja quantile_quantile() przedstawiona w poniższym kodzie). Ten wspólny interfejs pozwala nam używać tych strategii jako wtyczek, które można łatwo zastąpić, tak jak robimy to w odpowiednich funkcjach variable_histogram i variable_qqplot() (obie wykonują to samo wywołanie, ale w każdym przypadku używają innej strategii). Jak widać, inne szczegóły, które nie są częścią wspólnego interfejsu (na przykład main i 􀁙 xlab), są obsługiwane w kodzie każdej strategii. Moglibyśmy dodać je jako opcjonalne argumenty, gdybyśmy chcieli, ale nie jest to konieczne w tym przykładzie:

variable_historgram <- function(data, variable, save_to = „”){

save_png(data, variable, save_to, histgram_

}

histogram <- function(data, variable_ {

hist(data[, variable], main = „Histogram”, xlab = Proportion”]

)

variable_qqplot <- fution(data, variable, save_to = „”) {

save_png(data, variable, save+to, quantile_quatile)

}

quantile_quantile <- function(data, variable) {

qqnorm)data[, varaible[, main= „Normal  QQ-Plot for Proprotion”)

qqline(data[, variable])

}

Poniżej przedstawiono wykres do sprawdzania normalności proporcji:

quantile_quantile <- function(data, variable) {

qqnorm(data[, variable] , main = „Normal QQ- Plot for Proprotion”)

qqline(data[, variable])

}

Gdybyśmy chcieli udostępnić kod używany do tworzenia obrazów PNG z trzecią (lub więcej) strategiami, możemy po prostu dodać opakowanie strategii dla każdego nowego przypadku, nie martwiąc się o powielanie kodu, który tworzy obrazy PNG. Może się wydawać, że to nic wielkiego, ale wyobraź sobie, że kod użyty do utworzenia plików PNG był złożony i nagle znalazłeś błąd. Czego potrzebujesz, aby naprawić ten błąd? Cóż, musiałbyś udać się w każde miejsce, w którym zduplikowałeś kod i tam go naprawić. Wydaje się mało wydajne. Co się stanie, jeśli nie chcesz już zapisywać plików PNG, a zamiast tego chcesz zapisywać pliki JPG? Cóż, znowu musiałbyś iść wszędzie, gdzie zduplikowałeś swój kod i zmienić go.

Znowu niezbyt wydajne. Jak widać, ten sposób programowania wymaga niewielkiej inwestycji z góry (stworzenie wspólnych interfejsów i dostarczenie opakowań), ale korzyści z tego zwrócą się w ramach zaoszczędzonego czasu, trzeba zmienić kod, choćby raz , a także bardziej zrozumiały i prostszy kod. Jest to forma zarządzania zależnościami i jest to coś, czego powinieneś się nauczyć, aby stać się bardziej wydajnym programistą. Być może zauważyłeś, że w poprzednim kodzie mogliśmy uniknąć jednego wywołania funkcji, wywołując bezpośrednio funkcję save_png(). Jednak zrobienie tego wymagałoby od użytkownika znajomości dwóch rzeczy: funkcji save_png() do zapisywania obrazu i funkcji quantile_quantile() lub histogram() które tworzą wykresy, w zależności od tego, co próbowała wykreślić. To dodatkowe obciążenie dla użytkownika, choć pozornie nie jest problematyczne, może sprawić, że sytuacja będzie dla niej bardzo zagmatwana, ponieważ niewielu użytkowników jest przyzwyczajonych do wysyłania funkcji jako argumentów i musieliby znać dwie sygnatury funkcji zamiast jednej. Zapewnienie opakowania, którego podpis jest łatwy w użyciu, tak jak robimy to z variable_histogram() i variable_qqplot() ułatwia to użytkownikowi i pozwala nam rozszerzyć sposób, w jaki chcemy wyświetlać wykresy, na wypadek gdybyśmy chcieli to później zmienić bez zmuszania użytkownika do uczenia się nowej sygnatury funkcji. Aby faktycznie utworzyć wykresy, których szukamy, używamy następującego kodu:

variable_histogram(data = data, variable = „Proportion”)

variable_qqplot(data = data, variable = „Prorporti

Jak widać, histogram pokazuje przybliżony rozkład normalny lekko pochylony w prawo, ale możemy go łatwo zaakceptować jako normalny. Odpowiedni wykres kwantylowo-kwantylowy przedstawia te same informacje w nieco inny sposób. Linia, którą pokazuje, odpowiada kwantylom rozkładu normalnego, a kropki pokazują rzeczywisty rozkład danych. Im bliżej linii znajdują się te kropki, tym bliżej rozkładu zmiennej jest rozkład normalny. Jak widać, w przeważającej części Proportion ma rozkład normalny, a na skrajach widać niewielkie odchylenie, które prawdopodobnie wynika z tego, że nasza zmienna Proportion w rzeczywistości zmienna ma sztywne limity na 0 i 1. Jednakże możemy również zaakceptować ją jako rozkład normalny i możemy bezpiecznie przejść do następnego założenia.

Sprawdzimy normalność za pomocą dwóch różnych technik, aby zilustrować użycie techniki znanej jako wzorzec strategii, która jest częścią zestawu wzorców z programowania obiektowego. Na razie możesz myśleć o schemacie strategii jako o technice, która ponownie wykorzysta kod, który w przeciwnym razie zostałby zduplikowany i po prostu zmienia sposób wykonywania rzeczy zwanych strategią. W poniższym kodzie widać, że tworzymy funkcję o nazwie save_png(), która zawiera kod, który zostałby zduplikowany (zapisywanie plików PNG) i nie musi być. Będziemy mieć dwie strategie, w postaci funkcji, sprawdzania normalności danych – histogramy i wykresy kwantyl-kwantyl. Zostaną one przesłane za pomocą argumentu o dogodnej nazwie function_to_create_images. Jak widać, ten kod otrzymuje pewne dane, zmienną, która zostanie użyta dla wykresu, nazwę pliku obrazu oraz funkcję, która zostanie użyta do utworzenia wykresów. Ten ostatni parametr, funkcja, nie powinien być nieznany czytelnikowi, że możemy wysyłać funkcje jako argumenty i używać ich tak, jak robimy w tym kodzie wywołując je poprzez ich nową nazwę wewnątrz funkcji, function_to_create_images() w tym przypadku:

save_png <- function(data,variable, save_to, function_to_create_image){

if (not_empty(save_to)) png(save_to)

function_to_create_image(data, variable)

if (not_empty(save_to)) dev.off()

}

Teraz pokażemy kod, który będzie używał tej funkcji save_png() i hermetyzujemy wiedzę o funkcji używanej w każdym przypadku. W przypadku histogramów funkcja histohram() pokazana w poniższym kodzie po prostu opakowuje funkcję hist() używaną do tworzenia wykresu ze wspólnym interfejsem, który będzie również używany przez inne strategie (w tym przypadku funkcja quantile_quantile() przedstawiona w poniższym kodzie). Ten wspólny interfejs pozwala nam używać tych strategii jako wtyczek, które można łatwo zastąpić, tak jak robimy to w odpowiednich funkcjach variable_histogram i variable_qqplot() (obie wykonują to samo wywołanie, ale w każdym przypadku używają innej strategii). Jak widać, inne szczegóły, które nie są częścią wspólnego interfejsu (na przykład main i 􀁙 xlab), są obsługiwane w kodzie każdej strategii. Moglibyśmy dodać je jako opcjonalne argumenty, gdybyśmy chcieli, ale nie jest to konieczne w tym przykładzie:

variable_historgram <- function(data, variable, save_to = „”){

save_png(data, variable, save_to, histgram_

}

histogram <- function(data, variable_ {

hist(data[, variable], main = „Histogram”, xlab = Proportion”]

)

variable_qqplot <- fution(data, variable, save_to = „”) {

save_png(data, variable, save+to, quantile_quatile)

}

quantile_quantile <- function(data, variable) {

qqnorm)data[, varaible[, main= „Normal  QQ-Plot for Proprotion”)

qqline(data[, variable])

}

Poniżej przedstawiono wykres do sprawdzania normalności proporcji:

quantile_quantile <- function(data, variable) {

qqnorm(data[, variable] , main = „Normal QQ- Plot for Proprotion”)

qqline(data[, variable])

}

Gdybyśmy chcieli udostępnić kod używany do tworzenia obrazów PNG z trzecią (lub więcej) strategiami, możemy po prostu dodać opakowanie strategii dla każdego nowego przypadku, nie martwiąc się o powielanie kodu, który tworzy obrazy PNG. Może się wydawać, że to nic wielkiego, ale wyobraź sobie, że kod użyty do utworzenia plików PNG był złożony i nagle znalazłeś błąd. Czego potrzebujesz, aby naprawić ten błąd? Cóż, musiałbyś udać się w każde miejsce, w którym zduplikowałeś kod i tam go naprawić. Wydaje się mało wydajne. Co się stanie, jeśli nie chcesz już zapisywać plików PNG, a zamiast tego chcesz zapisywać pliki JPG? Cóż, znowu musiałbyś iść wszędzie, gdzie zduplikowałeś swój kod i zmienić go.

Znowu niezbyt wydajne. Jak widać, ten sposób programowania wymaga niewielkiej inwestycji z góry (stworzenie wspólnych interfejsów i dostarczenie opakowań), ale korzyści z tego zwrócą się w ramach zaoszczędzonego czasu, trzeba zmienić kod, choćby raz , a także bardziej zrozumiały i prostszy kod. Jest to forma zarządzania zależnościami i jest to coś, czego powinieneś się nauczyć, aby stać się bardziej wydajnym programistą. Być może zauważyłeś, że w poprzednim kodzie mogliśmy uniknąć jednego wywołania funkcji, wywołując bezpośrednio funkcję save_png(). Jednak zrobienie tego wymagałoby od użytkownika znajomości dwóch rzeczy: funkcji save_png() do zapisywania obrazu i funkcji quantile_quantile() lub histogram() które tworzą wykresy, w zależności od tego, co próbowała wykreślić. To dodatkowe obciążenie dla użytkownika, choć pozornie nie jest problematyczne, może sprawić, że sytuacja będzie dla niej bardzo zagmatwana, ponieważ niewielu użytkowników jest przyzwyczajonych do wysyłania funkcji jako argumentów i musieliby znać dwie sygnatury funkcji zamiast jednej. Zapewnienie opakowania, którego podpis jest łatwy w użyciu, tak jak robimy to z variable_histogram() i variable_qqplot() ułatwia to użytkownikowi i pozwala nam rozszerzyć sposób, w jaki chcemy wyświetlać wykresy, na wypadek gdybyśmy chcieli to później zmienić bez zmuszania użytkownika do uczenia się nowej sygnatury funkcji. Aby faktycznie utworzyć wykresy, których szukamy, używamy następującego kodu:

variable_histogram(data = data, variable = „Proportion”)

variable_qqplot(data = data, variable = „Prorporti

Jak widać, histogram pokazuje przybliżony rozkład normalny lekko pochylony w prawo, ale możemy go łatwo zaakceptować jako normalny. Odpowiedni wykres kwantylowo-kwantylowy przedstawia te same informacje w nieco inny sposób. Linia, którą pokazuje, odpowiada kwantylom rozkładu normalnego, a kropki pokazują rzeczywisty rozkład danych. Im bliżej linii znajdują się te kropki, tym bliżej rozkładu zmiennej jest rozkład normalny. Jak widać, w przeważającej części Proportion ma rozkład normalny, a na skrajach widać niewielkie odchylenie, które prawdopodobnie wynika z tego, że nasza zmienna Proportion w rzeczywistości zmienna ma sztywne limity na 0 i 1. Jednakże możemy również zaakceptować ją jako rozkład normalny i możemy bezpiecznie przejść do następnego założenia.

Podstawowym sposobem sprawdzenia założenia o liniowości jest wykonanie wykresu rozrzutu ze zmienną zależną na osi y i zmienną niezależną na osi x. Jeśli relacja wydaje się być liniowa, założenie jest sprawdzane. W każdym interesującym problemie niezwykle trudno jest znaleźć wykres punktowy, który pokazuje bardzo wyraźną zależność liniową, a jeśli tak się stanie, powinniśmy być trochę podejrzliwi i ostrożni z danymi. Aby uniknąć ponownego wynalezienia koła, użyjemy funkcji plot_scatterlot , którą stworzyliśmy wcześniej:

plot_scatterplot(

data = data,

var_x = „age_18to44”,

var_y = „Proportion”

var_olor = FALSE

regression = TRUE

)

plot_scatterplot (

data = data,

var_x = „Students”,

var_y = „Proportion”,

var_color= FALSE

regression = TRUE

)

Jak widać, wykres punktowy po lewej stronie pokazuje wyraźną zależność liniową, wraz ze wzrostem odsetka osób między 18 a 44 rokiem życia (age_18to44) odsetek osób na korzyść opuszczających UE (Proportion) spada. Po prawej stronie widzimy, że relacja wśród odsetka uczniów na oddziale (Students) i Proportion jest wyraźnie liniowy w obszarze początkowym (gdzie Students mieści się w przedziale od 0 do 20), potem też relacja wydaje się być liniowa, ale jest zanieczyszczona obserwacjami z bardzo wysokim odsetkiem studentów. Jednak nadal możemy założyć liniową zależność między Student i Proportion. Kiedy robimy wielokrotną regresję liniową, tak jak tutaj robimy, założenie powinno zostać sprawdzone dla pozostałych zmiennych, które pomijamy tutaj, aby zachować miejsce, ale zachęcamy do tego. Należy pamiętać, że we wszystkich z nich bardzo trudno jest znaleźć zależność liniową, a to założenie jest głównie wskaźnikiem mocy predykcyjnej zmiennej w regresji. Dopóki relacja wydaje się być nieco liniowa, wszyscy powinniśmy być ustawione.

Modele liniowe, jak w przypadku każdego rodzaju modeli, wymagają sprawdzenia ich założeń, aby uzasadnić ich zastosowanie. Dokładność i możliwość interpretacji wyników wynika z przestrzegania założeń modelu. Czasami będą to rygorystyczne założenia w tym sensie, że jeśli nie są one ściśle przestrzegane, to model w ogóle nie jest uznawany za ważny. Innym razem będziemy pracować z bardziej elastycznymi założeniami, w których w grę wchodzi stopień kryteriów od analityka. W przypadku modeli liniowych niektóre z podstawowych założeń:

Liniowość: istnieje liniowa zależność między zmiennymi

Normalność: reszty mają rozkład normalny

Homoskedastyczność: reszty mają stałą wariancję

Brak kolinearności: zmienne nie są wzajemnymi kombinacjami liniowymi

Niezależność: reszty są niezależne lub przynajmniej nieskorelowane

Pokażemy, jak krótko sprawdzić cztery z nich: liniowość, normalność, homoskedastyczność i brak kolinearności. Powinniśmy wspomnieć, że założenie niezależności jest prawdopodobnie najtrudniejszym do przetestowania założeniem i ogólnie można sobie z nim poradzić, kierując się zdrowym rozsądkiem i zrozumieniem, w jaki sposób zebrano dane. Nie będziemy się tym zajmować, ponieważ jest to bardziej w statystykacha a chcemy, skupić się na technikach programowania.

Zanim będziemy mogli dokonać jakichkolwiek prognoz, musimy określić model i wyszkolić go z naszymi danymi szkoleniowymi (data_train), aby nauczył się, jak dostarczyć nam prognozy, których szukamy. Oznacza to, że rozwiążemy problem optymalizacji, który generuje określone liczby, które będą używane jako parametry dla prognoz naszego modelu. R bardzo ułatwia nam wykonanie takiego zadania. Standardowym sposobem określenia modelu regresji liniowej w R jest użycie funkcji lm() z modelem, który chcemy zbudować, wyrażonej jako formuła i dane, które mają być użyte, i zapisanie go do obiektu (w tym przypadku fit), które możemy wykorzystać do szczegółowego zbadania wyników. Na przykład najprostszy model, jaki możemy zbudować, to taki z pojedynczym regresorem (zmienną niezależną) w następujący sposób:

fit <- lm(Proportion ~ Students, data_train)

W tym prostym modelu poinformowalibyśmy R, że chcemy przeprowadzić regresję, w której spróbujemy wyjaśnić zmienną Proportion, używając tylko zmiennej Studets w danych. Ten model jest zbyt prosty, co się stanie, jeśli będziemy chcieli dołączyć drugą zmienną? Cóż, możemy to dodać, używając znaku plus (+) po naszych innych regresorach. Na przykład (pamiętaj, że spowoduje to zastąpienie poprzedniego obiektu fit nowymi wynikami, więc jeśli chcesz zachować oba z nich, upewnij się, że nadasz obiektom wynikowym inne nazwy):

fit <- lm(Proportion ~ Students + Age+18to44, data_train)

To może być lepszy sposób wyjaśnienia zmiennej Proportio, ponieważ pracujemy z większą ilością informacji. Należy jednak pamiętać o problemie kolinearności; prawdopodobne jest, że im wyższy procent uczniów znajduje się na oddziale (Students), tym wyższy odsetek stosunkowo młodych ludzi (Age_18to44), co oznacza, że ​​możemy nie być dodaniem niezależnych informacji do regresji. Oczywiście w większości sytuacji nie jest to kwestia binarna, jest to kwestia stopnia i analityk musi być w stanie sobie z nimi poradzić. Dowiemy się więcej na ten temat, sprawdzając założenia modelu w następnej sekcji. Na razie wróćmy do programowania, dobrze? A co, jeśli chcemy uwzględnić wszystkie zmienne w danych? Cóż, mamy dwie opcje, dołącz wszystkie zmienne ręcznie lub użyj do tego skrótu R:

# manually

fit <- lp(Proportion ~ ID + RegionName + NVotes + Leave + Resident + Households + White + Owned + OwnedOutright + SocialRent + PrivateRent + Students + Unemp + UnempRate_EA + HigherOccup + Densoty + Deprived + MultiDepriv + Age_18to44 + Age_45plus + NonWhite + HihghEducationLevel + LowEducationLevel , data_train)

# R’s shortcut

fit <- lm(Proportion ~ ./, data_trai)

Te dwa modele są dokładnie takie same. Jest jednak kilka subtelnych punktów, o których musimy wspomnieć. Po pierwsze, podczas ręcznego określania modelu musieliśmy wyraźnie pozostawić zmienną Proprotion poza regresorami (zmienne po symbolu 􀁟), aby podczas wykonywania regresji nie wystąpił błąd ( nie miałoby sensu, gdyby R pozwolił nam spróbować wyjaśnić zmienną Proportion za pomocą tej samej zmiennej Proprotion i innych rzeczy). Po drugie, jeśli popełnimy jakieś literówki podczas pisania nazw zmiennych, otrzymamy błędy, ponieważ te nazwy nie będą obecne w nazwach zmiennych (jeśli przez przypadek literówka faktycznie odnosi się do innej istniejącej zmiennej w danych, może to być trudny błąd rozpoznać chorobę). Po trzecie, w obu przypadkach lista regresorów zawiera zmienne, których nie powinno tam być, takie jak ID, RegionName, NVotes, Leave  i Vote . W przypadku of ID nie ma sensu uwzględnienie tej zmiennej w analizie, ponieważ nie zawiera żadnych informacji dotyczących Proprotion, jest to tylko identyfikator. W przypadku RegionName jest to zmienna kategorialna, więc regresja przestałaby być standardową regresją wielokrotną liniową, a R automatycznie sprawiłoby, że działałaby dla nas, ale jeśli nie rozumiemy, co robimy może dawać mylące wyniki. W tym przypadku chcemy pracować tylko ze zmiennymi numerycznymi, abyśmy mogli łatwo usunąć to z przypadku ręcznego, ale nie możemy tego zrobić w przypadku skrótu. Wreszcie, w przypadku NVotes, Leave i Vote zmienne te wyrażają te same informacje w nieco ten sam sposób, więc nie powinny być uwzględniane, ponieważ mielibyśmy wielokoliniowość problem. Powiedzmy, że ostateczny model, z którym chcemy pracować, zawiera wszystkie prawidłowe zmienne numeryczne:

fit <- lm(Proportion ~ Residents + Households + White + Owned + OwnedOutright + SocialRent + PrivateRent + Students _ Unem + UnempRate_EA + HigherOccup + Density + Deprived + MultiDepriv + Age_18to44 + Age_45plus + NonWhite _ HighEducationaLevel + LowEducationaLevel , data_train)

Aby szczegółowo przyjrzeć się wynikom, używamy funkcji summary()na obiekcie fit:

summary(fit)

#>

#> Call:

#> lm(formula = Proportion ~ Residents + Households + White + Owned +

#> OwnedOutright + SocialRent + PrivateRent + Students + Unemp +

#> UnempRate_EA + HigherOccup + Density + Deprived + MultiDepriv +

#> Age_18to44 + Age_45plus + NonWhite + HighEducationLevel +

#> LowEducationLevel, data = data_train)

#>

#> Residuals:

#> Min 1Q Median 3Q Max

#> -0.21606 -0.03189 0.00155 0.03393 0.26753

#>

#> Coefficients:

#> Estimate Std. Error t value Pr(>|t|)

#> (Intercept) 3.30e-02 3.38e-01 0.10 0.92222

#> Residents 7.17e-07 2.81e-06 0.26 0.79842

#> Households -4.93e-06 6.75e-06 -0.73 0.46570

#> White 4.27e-03 7.23e-04 5.91 6.1e-09 ***

#> Owned -2.24e-03 3.40e-03 -0.66 0.51071

#> OwnedOutright -3.24e-03 1.08e-03 -2.99 0.00293 **

#> SocialRent -4.08e-03 3.60e-03 -1.13 0.25847

#> PrivateRent -3.17e-03 3.59e-03 -0.89 0.37629

#> Students -8.34e-04 8.67e-04 -0.96 0.33673

#> Unemp 5.29e-02 1.06e-02 5.01 7.3e-07 ***

#> UnempRate_EA -3.13e-02 6.74e-03 -4.65 4.1e-06 ***

#> HigherOccup 5.21e-03 1.24e-03 4.21 2.9e-05 ***

#> Density -4.84e-04 1.18e-04 -4.11 4.6e-05 ***

#> Deprived 5.10e-03 1.52e-03 3.35 0.00087 ***

#> MultiDepriv -6.26e-03 1.67e-03 -3.75 0.00019 ***

#> Age_18to44 3.46e-03 1.36e-03 2.55 0.01117 *

#> Age_45plus 4.78e-03 1.27e-03 3.75 0.00019 ***

#> NonWhite 2.59e-03 4.47e-04 5.80 1.1e-08 ***

#> HighEducationLevel -1.14e-02 1.14e-03 -9.93 < 2e-16 ***

#> LowEducationLevel 4.92e-03 1.28e-03 3.85 0.00013 ***

#> —

#> Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ‘ 1

#> Residual standard error: 0.0523 on 542 degrees of freedom

#> Multiple R-squared: 0.868, Adjusted R-squared: 0.863

#> F-statistic: 187 on 19 and 542 DF, p-value: <2e-16

Te wyniki mówią nam, które polecenie zostało użyte do utworzenia naszego modelu, co jest przydatne, gdy tworzysz różne modele i chcesz szybko poznać model powiązany z wyświetlanymi wynikami. Pokazuje również pewne informacje o rozkładzie reszt. Następnie pokazuje wyniki regresji dla każdej zmiennej używanej w trybie. Otrzymujemy nazwę zmiennej ((Intercept) to punkt przecięcia ze standardową regresją liniową używaną w specyfikacji modelu), estymację współczynnika dla zmiennej, błąd standardowy, statystykę t, wartość p- wartość i wizualne przedstawienie wartości p przy użyciu gwiazdek dla kodów istotności. Na końcu wyników widzimy inne wyniki związane z modelem, w tym R-kwadrat i statystykę F. Jak wspomniano wcześniej, nie będziemy wchodzić w szczegóły dotyczące tego, co każdy z nich oznacza, a my nadal będziemy się koncentrować na technikach programowania.. Teraz, gdy mamy już dopasowany model gotowy w obiekcie fit, możemy go użyć do prognozowania. Aby to zrobić, używamy funkcji predict() z obiektem fit i danymi, dla których chcemy wygenerować prognozy, w naszym przypadku data_test. To zwraca wektor prognoz, które przechowujemy w obiekcie predictions. Otrzymamy jedną prognozę dla każdej obserwacji w obiekcie data_test:

preditions <- predict(fit, data_test)

Te przewidywania można zmierzyć pod kątem dokładności, tak jak zrobimy to w dalszej części tego rozdziału. Na razie wiemy, jak łatwo generować prognozy za pomocą R.

Abyśmy mogli zmierzyć predykcyjną dokładność naszych modeli, musimy użyć pewnych obserwacji, aby zweryfikować nasze wyniki. Oznacza to, że nasze dane zostaną podzielone na trzy różne grupy:

* Dane treningowe

* Dane testowe

* Przewidywanie danych

Dane przewidywane to dane, dla których nie mamy pełnych przypadków, a konkretnie są to okręgi wyborcze, dla których zmienne Vote i Proportion mają  wartości NA. Naszym ostatecznym celem jest dostarczenie przewidywań dla zmiennych Proprotion i Vote tych okręgów wyborczych na podstawie tego, czego możemy się nauczyć od innych okręgów, dla których mamy dane dla tych zmiennych. zrobić pod koniec części. Dane zawierające kompletne przypadki zostaną podzielone na dwie części, dane treningowe i testowe. Dane szkoleniowe służą do wydobywania wiedzy i uczenia się zależności między zmiennymi. Testowanie jest traktowane tak, jakby miało wartości NA dla Proportion i Vote, i tworzymy dla nich prognozy. Te przewidywania są następnie porównywane z rzeczywistymi wartościami w odpowiednich obserwacjach, co pomaga nam zrozumieć, jak dobre są nasze przewidywania w sposób obiektywny, ponieważ te obserwacje nigdy nie są widoczne przez wytrenowane modele. Stworzyliśmy dane przewidywania w poprzedniej sekcji i nazwaliśmy je data_incomplete. Do tworzenia danych treningowych i testowych używamy funkcji sample(). Jako dane wejściowe przyjmie listę liczb, z których wybierze określoną liczbę wartości (size). Lista liczb będzie wynosić od 1 do całkowitej liczby obserwacji dostępnych w danych z kompletnymi przypadkami. Określamy liczbę obserwacji, które zostaną wybrane do danych uczących, jako około 70% całkowitej liczby dostępnych obserwacji i używamy argumentu replalce = FALSE, aby określić, że wybrane obserwacje nie można powielać (unikając zastępowania próbki). Na dane testowe składają się pozostałe 30% obserwacji. Ponieważ sample jest wektorem boolowskim, który zawiera wartość TRUE lub FALSE dla każdej obserwacji, aby określić, czy powinna być uwzględniona, czy nie, możemy zanegować wektor, aby wybrać drugą część danych przez dołączenie znaku minus (-) do wektora binarnego, co w efekcie sprawia, że ​​każda wartość TRUE jest wartością FALSEi odwrotnie. Aby to zrozumieć, spójrzmy na następujący kod:

set.seed(12345)

n<- nrow(data)

sample <- sample(1:n, size  = roud(0.7 * n), replace = FALSE)

data_train <- data[ sample, ]

data_test <- data[-sample]

Gdybyśmy robili ten proces kilka razy, stwierdzilibyśmy, że za każdym razem otrzymujemy różne próbki do zestawów treningowych i testowych, co może nas mylić co do naszych wyników. Dzieje się tak, ponieważ funkcja sample() jest stochastyczna, co oznacza, że ​​użyje generatora liczb pseudolosowych, aby dokonać wyboru za nas (komputery nie mogą generować rzeczywistej losowości, symulują liczby, które wydają się losowe, mimo że nie są, dlatego nazywa się to pseudolosowym). Jeśli chcemy, aby nasz proces był powtarzalny, co oznacza, że ​​za każdym razem, gdy go uruchamiamy, wybierane są dokładnie te same próbki, to musimy określić początkowe ziarno przed zastosowaniem tego procesu do wstępnego uwarunkowania generatora liczb pseudolosowych. Aby to zrobić, musimy przekazać liczbę całkowitą do funkcji set.seed(), tak jak robimy to na początku fragmentu kodu. Argument początkowy musi pozostać niezmienny, aby odtworzyć te same próbki, a gdy jest na miejscu, za każdym razem, gdy generujemy próbkę losową, otrzymujemy tę samą próbkę, aby nasze wyniki były powtarzalne.

Jak to zwykle bywa w przypadku analizy danych, pierwszym krokiem jest zrozumienie danych, z którymi będziemy pracować. W tym przypadku dane są takie same jak wcześniej, a niektóre z jego głównych cech już zrozumieliśmy. Przede wszystkim zrozumieliśmy, że wiek, wykształcenie i rasa mają znaczący wpływ na skłonność do głosowania za opuszczeniem lub pozostaniem Wielkiej Brytanii w UE. Tu skupimy się na wykorzystaniu modeli liniowych do przewidywania zmiennych Proportion i Vote, które zawierają procent głosów za opuszczeniem UE oraz to, czy okręg wyborczy miał więcej głosów odpowiednio dla „Leave” lub „Remain”. Obie zmienne mają podobne informacje, z tą różnicą, że jedna jest numeryczną zmienną ciągłą o wartościach od 0 do 1 (Proportio), a druga jest zmienną kategorialną z dwiema kategoriami (Vote z kategoriami Leave i Remain). Zachowamy obserwacje, które zawierają pełne obserwacje w obiekcie data i obserwacje, w których brakuje wartości dla zmiennych Proprotio i Vote  w obiekcie data_icomplete (będziemy przewidywać je w dalszej części). Funkcje prepare_data(), adjust_data() i get_numerical_variables() pochodzą z wcześniejszej części, więc możesz rzucić okiem, jeśli nie masz pewności, co robią. Zasadniczo ładują dane dostosowaną wersją, którą stworzyliśmy, kompresując dane rozłożone na różne zmienne dotyczące wieku, wykształcenia i rasy:

data <- adjust_datat(prepare_data(„./data_brexit_referendum.csv”))

data_incomplete <- data[!complete.cases(data),]

data <- data[ complete.cases(data), ]

numerical_variables <- get_numerical_variable_names(data)