Teraz, gdy sprawdziliśmy założenia naszego modelu, przechodzimy do pomiaru jego mocy predykcyjnej. Aby zmierzyć naszą dokładność predykcyjną, użyjemy dwóch metod, jednej dla danych liczbowych (Proportion), a drugiej dla danych jakościowych (Vote). Wiemy, że zmienna Vote jest transformacją ze zmiennej Proprotion, co oznacza, że mierzymy te same informacje na dwa różne sposoby. Jednak zarówno dane liczbowe, jak i jakościowe są często spotykane w analizie danych, dlatego chcieliśmy tutaj pokazać oba podejścia. Obie funkcje, score_proportion() (numeryczna) i score_votes () (kategoryczna) otrzymujemy dane, których używamy do testowania i prognozy dla każdej obserwacji w danych testowych, które pochodzą z modelu, który zbudowaliśmy w poprzednich sekcjach.
W przypadku liczbowym score_proprotios() oblicza wynik przy użyciu następującego wyrażenia:
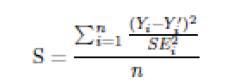
Tutaj Y_i to rzeczywista wartość zmiennej odpowiedzi dla i-tej obserwacji w danych testowych, Y’_i to nasza prognoza dla tej samej obserwacji, SE to błąd standardowy naszej prognozy, a n to liczba obserwacji w testowaniu dane. To równanie ustala, że wynik, który chcemy zminimalizować, jest średnią studentyzowanych reszt. Jak zapewne wiesz, reszty studenckie to reszty podzielone przez miarę błędów standardowych. Ta formuła daje nam średnią miarę tego, jak blisko jesteśmy do prawidłowego przewidzenia wartości obserwacji w stosunku do wariancji obserwowanej dla tego zakresu danych. Jeśli mamy wysoki stopień wariancji (powodujący błędy o wysokim standardzie), nie chcemy być zbyt rygorystyczni w przewidywaniu, ale jeśli znajdujemy się w obszarze o niskiej wariancji, chcemy mieć pewność, że nasze przewidywania są bardzo dokładne:
score_proprotios <- funtio(data_test, predictios){
# se := stadad errors
se <- predictios$se.fit
real <- data_test$Proprotion
predicted <- predictions$fit
retur(sum((real – predicted)^2 / se^2) . nrow(datat))
}
W przypadku kategorycznym score_votes() oblicza wynik, po prostu licząc, ile razy nasze przewidywania wskazywały na właściwą kategorię, którą chcemy zmaksymalizować. Robimy to, używając najpierw tego samego mechanizmu klasyfikacji (jeśli przewidywane Proprotion jest większe niż 0,5, to klasyfikujemy go jako glos „Leave” i odwrotnie) i porównujemy wartości kategoryczne. Wiemy, że suma wektora boolowskiego będzie równa liczbie TRUE wartości i właśnie tego używamy w wyrażeniu sum(real == predictes:
score_votes <- function (data_test, preditions) {
real <- datta_test$Vote
predicted <- ifelse(predictions$fit > 0.5 , „Leave”, „Remain”)
return(sum(real == predicted))
}
Aby przetestować wyniki naszego modelu, wykonujemy następujące czynności:
predictios <- predict(fit, data_test, se.fit = TRUE)
score_proportions(data_test, predictions)
#> [1] 10,66
score_votes(data_test, predictions)
#> [1] 216
nrow(data_test)
#> [1] 241
W przypadku funkcji score_votes() sama miara mówi nam, jak dobrze sobie radzimy z naszymi przewidywaniami, ponieważ możemy wziąć liczbę poprawnych przewidywań (wynik wywołania funkcji , czyli 216) i podziel go przez liczbę obserwacji (wierszy) w obiekcie data_test (czyli 241). Daje nam to precyzję 89%. Oznacza to, że gdybyśmy otrzymali dane od regresorów, ale nie wiemy, jak faktycznie głosował podopieczny, w 89% przypadków przedstawilibyśmy prognozę, czy chcą odejść, czy pozostać na UE, co byłoby poprawne. To całkiem nieźle, jeśli o mnie chodzi. W przypadku funkcji score_proportions(), ponieważ używamy bardziej abstrakcyjnej miary, aby wiedzieć, jak dobrze sobie radzimy, chcielibyśmy aby porównać to z wynikami innych modeli i uzyskać względne poczucie mocy predykcyjnej modelu, i właśnie to zrobimy w następnych sekcjach.