Aby sprawdzić, czy nie ma kolinearności, możemy użyć wielu różnych technik. Na przykład dla osób zaznajomionych z algebrą liniową numer warunku jest miarą osobliwości macierzy, gdzie osobliwość oznaczałaby doskonałą współliniowość między zmiennymi towarzyszącymi. Ta liczba może stanowić miarę tej kolinearności. Inną techniką jest użycie współczynnika inflacji wariancji, który jest bardziej formalną techniką, która zapewnia miarę wzrostu wariancji regresji z powodu kolinearności. Innym i bardziej powszechnym sposobem sprawdzenia tego są proste korelacje. Czy są jakieś zmienne silnie skorelowane między sobą w tym sensie, że może istnieć między nimi bezpośredni związek? Jeśli tak, to możemy mieć problem z współliniowością. Poniższy kod pokazuje, jak działają korelacje w języku R:
library(corrplot)
corrplot(corr = cor(data[, numerical_variables]), tl.col = „black”, tl.cex = 0.6)
Jak widać, silne korelacje (dodatnie lub ujemne) występują wewnątrz grup, a nie między grupami, co oznacza, że zmienne, które mierzą to samo na różne sposoby, wydają się być wysoce skorelowane, podczas gdy zmienne, które mierzą różne rzeczy, nie wydają się być wysoce skorelowane.
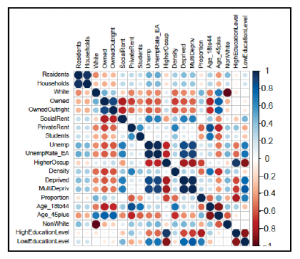
Na przykład Age_18to44 i Age_45plus to zmienne mierzące wiek i spodziewamy się, że będą miały negatywną relację, ponieważ im wyższy odsetek młodych ludzi na oddziale z konieczności odsetek osób starszych jest niższy. Ta sama zależność jest widoczna w grupie mieszkań (Owned, OwedOutright, SocialRent i PrivateRent ), grupa zatrudnionych (Unemp, UnempRate_EA i HigherOccup), grupa potrzebująca (Deprived i MultiDepriv), grupa etniczna (White i NonWhite), grupa zamieszkania (Residet i Housholds) oraz grupę edukacyjną (LowEducationLevel i HighEducationLevel). Jeśli wybierzesz zmienne należące do różnych grup, liczba silnych korelacji jest znacznie niższa, ale istnieje. Na przykład HigherOccup jest silnie skorelowane z HighEducatioLevel i LowEducatioLevel, pozytywnie i odpowiednio negatywnie. Wydaje się również, że zmienne w grupie mieszkaniowej są skorelowane ze zmiennymi w grupie wiekowej. Tego typu relacje są oczekiwane i naturalne, ponieważ osoby z wyższym wykształceniem będą miały zapewne lepszą pracę, a młodych ludzi prawdopodobnie jeszcze nie stać na mieszkanie, więc wynajmują. Jako analitycy możemy założyć, że zmienne te w rzeczywistości mierzą różne aspekty społeczeństwa i kontynuować naszą analizę. Jednak są to nadal rzeczy, o których warto pamiętać podczas interpretacji wyników. Możemy również chcieć uwzględnić tylko jedną zmienną w każdej grupie, aby uniknąć kolinearności między grupami, ale unikniemy tych zawiłości i będziemy kontynuować nasza analiza na razie. Regresja liniowa jest jednym z tych typów modeli, które wymagają od analityka przyjęcia lub odrzucenia kryteriów. W naszym konkretnym przypadku wydaje się, że założenia naszego modelu są wystarczająco słuszne i możemy go bezpiecznie wykorzystać do dostarczenia wiarygodnych prognoz, tak jak to zrobimy w następnych sekcjach