Analiza głównych składowych (PCA) to technika redukcji wymiarowości, która jest szeroko stosowana w analizie danych, gdy istnieje wiele zmiennych numerycznych, z których niektóre mogą być skorelowane, i chcielibyśmy zmniejszyć liczbę wymiarów wymaganych do zrozumienia danych. Pomocne może być zrozumienie danych, ponieważ myślenie w więcej niż trzech wymiarach może być problematyczne, a także przyspieszenie algorytmów wymagających dużej mocy obliczeniowej, zwłaszcza w przypadku dużej liczby zmiennych. Dzięki PCA możemy wyodrębnić większość informacji tylko do jednej lub dwóch zmiennych skonstruowanych w bardzo specyficzny sposób, tak aby wychwytywały większość wariancji, a jednocześnie miały dodatkową korzyść w postaci braku korelacji między nimi przez konstrukcję.
Pierwszy główny składnik to liniowa kombinacja oryginalnych zmiennych, która oddaje maksymalną wariancję (informacje) w zbiorze danych. Żaden inny składnik nie może mieć większej zmienności niż pierwszy składnik główny. Następnie druga składowa główna jest ortogonalna do pierwszej i jest obliczana w taki sposób, aby uchwycić maksymalną wariancję pozostałą w danych. I tak dalej. Fakt, że wszystkie zmienne są kombinacjami liniowymi, które są między sobą ortogonalne, jest kluczem do ich nieskorelowania między sobą.
Wystarczy mówić o statystykach; przejdźmy do programowania! Wykonując PCA w R mamy wiele funkcji, które mogą wykonać to zadanie. Aby wspomnieć o niektórych z nich, mamy prcomp() i princom() z pakietu stats (wbudowanego), PCA() z pakietu FactoMineR , dudi.pca() z pakietu ade4 i acp() z pakietu amap. W naszym przypadku użyjemy funkcji prcomp() wbudowanej w R. Aby wykonać PCA, użyjemy skorygowanych danych z poprzedniej sekcji. Najpierw usuwamy zmienne numeryczne, które są skorelowane z Proportion. Następnie wykonujemy PCA, wysyłając dane liczbowe do funkcji prcomp(), a także niektóre parametry normalizacji. center . = TRUE odejmie od siebie średnią każdej zmiennej, oraz scale. = TRUE sprawi, że wariancja każdej zmiennej będzie jednolita, skutecznie normalizując dane. Normalizacja danych jest bardzo ważna podczas wykonywania PCA, ponieważ jest to metoda wrażliwa na skale:
numerical_variables_adjusted[[„Votes”]] <- FALSE
numerical_varaibles_adjusted[[„Leave”]] <- FALSE
data_numeircal_adjusted <- data_adjusted[, numerical_variables_adjusted]
pca <- promp(data_numerical_adjusted, center = TRUE, scale. = TRUE)
pca
#> Odchylenia standardowe (1, .., p = 21):
#> [1] 2,93919 2,42551 1,25860 1,13300 1,00800 0,94112 0,71392 0,57613
#> [9] 0,54047 0,44767 0,37701 0,30166 0,21211 0,17316 0,13759 0,11474
#> [17] 0,10843 0,09797 0,08275 0,07258 0,02717
#>
#> Obrót (n x k) = (21 x 21):
#> PC1 PC2 PC3 PC4 PC5
#> ID 0,008492 -0,007276 0,14499 0,174484 -0,82840
#> Mieszkańcy 0,205721 0,004321 0,54743 0,303663 0,06659
#> Gospodarstwa domowe 0,181071 0,008752 0,49902 0,470793 0,13119
#> AdultMeanAge -0,275210 0,192311 0,14601 -0,011834 0,12951
#> Biały -0,239842 0,112711 -0,25766 0,471189 -0,02500
#> Posiadane -0,289544 0,085502 0,26954 -0,179515 -0,11673
(Obcięte wyjście)
Kiedy wyświetlamy obiekt pca, możemy zobaczyć odchylenia standardowe dla każdej zmiennej, ale co ważniejsze, możemy zobaczyć wagi używane dla każdej zmiennej do utworzenia każdego głównego składnika. Jak widzimy, gdy spojrzymy na pełną wydajność naszego komputera, wśród najważniejszych wag (największych wartości bezwzględnych) mamy zmienne wieku i pochodzenia etnicznego, a także inne, takie jak posiadanie domu. Jeśli chcesz uzyskać wartość osi dla każdej obserwacji w nowym układzie współrzędnych złożonym z głównych składowych, po prostu musisz pomnożyć każdą obserwację w swoich danych (każdy wiersz) przez odpowiednie wagi z macierzy rotacji z obiektu pca (pca$rotation). Na przykład, aby wiedzieć, gdzie należy umieścić pierwszą obserwację w danych w odniesieniu do drugiego głównego składnika, możesz skorzystać z:
as.matrix(data_numerical_adjusted[1, ]) %*% pca$rotation [, 1]
Ogólnie rzecz biorąc, możesz zastosować operacje na macierzach, aby uzyskać współrzędne dla wszystkich obserwacji w danych w odniesieniu do wszystkich głównych składników w obiekcie , używając następującego wiersza, który wykona mnożenie macierzy. Pamiętaj, że nie musisz tego robić samodzielnie, ponieważ R zrobi to automatycznie podczas analizy wyników.
as.matrix(data_numerical_adjusted) %*% pca$rotation
Kiedy patrzymy na podsumowanie pca, możemy zobaczyć odchylenia standardowe dla każdego głównego składnika, a także jego proporcję uchwyconej wariancji i jej akumulację. Informacje te są przydatne przy podejmowaniu decyzji, ile głównych składników powinniśmy zachować do końca analizy. W naszym przypadku okazuje się, że mając tylko pierwsze dwa główne składniki, uchwyciliśmy około 70 procent informacji zawartych w danych, co w naszym przypadku może być wystarczające. Liczbę 70% można uzyskać, dodając wartość Proportion of variance dla głównych składników, które chcemy rozważyć (w kolejności i zaczynając od PC1). W tym przypadku, jeśli dodamy Proportion of variance dla PC1 i PC2, otrzymamy 0,411$ + 0,280 = 0,691$, czyli prawie 70 proc. Zauważ, że możesz po prostu spojrzeć na Cumulative proportion do znalezienia tej liczby bez konieczności samodzielnego obliczania sumy, ponieważ gromadzi ona Proportion of variance stopniowo, zaczynając od PC1. Zastanów się przez chwilę, jak potężna jest ta technika: mając tylko dwie zmienne, jesteśmy w stanie uchwycić 70 procent informacji zawartych w pierwotnych 40 zmiennych:
summary(pca)
#> Znaczenie komponentów:
#> PC1 PC2 PC3 PC4 PC5 PC6 PC7
#> Odchylenie standardowe 2,939 2,426 1,2586 1,1330 1,0080 0,9411 0,7139
#> Odsetek wariancji 0,411 0,280 0,0754 0,0611 0,0484 0,0422 0,0243
#> Skumulowana proporcja 0,411 0,692 0,7670 0,8281 0,8765 0,9186 0,9429
#> PC8 PC9 PC10 PC11 PC12 PC13
#> Odchylenie standardowe 0,5761 0,5405 0,44767 0,37701 0,30166 0,212 11
#> Odsetek wariancji 0,0158 0,0139 0,00954 0,00677 0,00433 0,00214
#> Skumulowana proporcja 0,9587 0,9726 0,98217 0,98894 0,99327 0,99541
#> PC14 PC15 PC16 PC17 PC18 PC19
#> Odchylenie standardowe 0,17316 0,1376 0,11474 0,10843 0,09797 0,08275
#> Proporcja wariancji 0,00143 0,0009 0,00063 0,00056 0,00046 0,00033
#> Łączna proporcja 0,99684 0,9977 0,99837 0,99893 0,99939 0,99971
(Obcięte wyjście)
Na powyższym wykresie widzimy wariancje (w postaci kwadratów odchyleń standardowych) z wyników summary(pca). Widzimy, jak każdy kolejny składnik główny oddaje mniejszą wartość całkowitej wariancji:
plot(pca, type = „1” , main = „Principal Components’ Variaces”)
Wreszcie, poniższy wykres przedstawia wykres rozrzutu obserwacji (punktów) oddziału na płaszczyźnie utworzonej przez dwa główne składniki z naszej analizy; nazywa się to biplot.
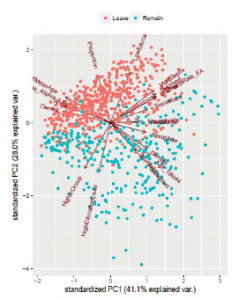
Ponieważ te dwa główne komponenty są tworzone jako liniowe kombinacje oryginalnych zmiennych, potrzebujemy pewnych wskazówek przy ich interpretacji. Dla ułatwienia strzałki wskazują kierunek przyporządkowania tej zmiennej do głównej osi składowej. Im dalej strzałka od środka, tym silniejszy wpływ na główne składniki. Dzięki temu biplotowi widzimy, że Proportion jest silnie powiązany z wychowankami, którzy głosowali za opuszczeniem UE, co jest oczywiste, ponieważ jest to konstrukcyjne. Jednak widzimy też inne interesujące relacje. Na przykład, poza efektami, które do tej pory stwierdziliśmy (wiek, wykształcenie i pochodzenie etniczne), osoby posiadające własne domy również są nieco powiązane z większą skłonnością do głosowania za opuszczeniem UE. Z drugiej strony nieznaną wcześniej relacją jest fakt, że im gęstsza jest populacja podopiecznego (pomyśl o miastach), tym bardziej prawdopodobne jest, że będą głosować za pozostaniem w UE:
library(ggbiplot)
biplot <- ggbiplot(pca, groups – data$Vote)
biplot <- biplot + scale_color_disrete(name = „ „)
biplot <- biplot + theme(legend.position = „top”, legend.discretio = „horizontal”)
print(biplot)