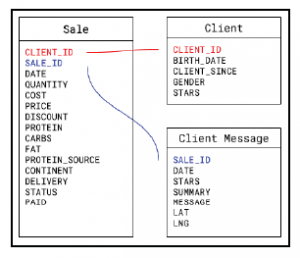
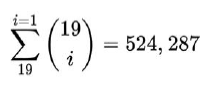Pierwszą rzeczą, którą musimy zrobić, jest opracowanie sposobu uzyskiwania kombinacji regresorów, które chcemy przetestować. Ponieważ jest to problem kombinatoryczny, liczba kombinacji jest wykładnicza wraz z liczbą dostępnych opcji. W naszym przypadku, przy 19 dostępnych zmiennych, liczba możliwych modeli jest sumą liczby modeli, które możemy utworzyć za pomocą jednego regresora oraz liczby modeli, które możemy utworzyć za pomocą dwóch regresorów itd., Aż zsumujemy liczbę modeli, które możemy stworzyć ze wszystkimi 19 regresorami. Oto jaka jest suma:
Oczywiście obliczanie tak wielu modeli, choć łatwych dla komputera, może trochę potrwać, dlatego chcemy ograniczyć minimalną i maksymalną liczbę regresorów dozwolonych w kombinacjach. W tym celu określamy minimalny i maksymalny procent regresorów, które zostaną uwzględnione w parametrach min_percentage i max_percentage, odpowiednio. W naszym przypadku, jeśli podamy min_percentage = 0.9 i max_percentage = 1 prosimy o podanie wszystkich kombinacji zawierających od 17 do 19 regresorów, co daje w sumie 191 modeli. Wyobraź sobie, ile czasu zajęłoby Ci ręczne wygenerowanie 191 specyfikacji modelu! Miejmy nadzieję, że myślenie o tym uświadomi ci siłę tej techniki.
Na początek tworzymy funkcję generate_combinations_unvectorized(), która wyświetli listę z wszystkimi możliwymi kombinacjami dla parametrów variable oraz min_percentage i max_percentage wspomnianych wcześniej. Pierwszą rzeczą, jaką robimy, jest usunięcie zmiennej Proportion, określając ją jako FALSE w wektorze varaibles (W tym miejscu obiekt variables odpowiada obiektowi numerial_variables, ale dostosowaliśmy jego nazwę w ramach tej funkcji, aby była bardziej czytelna). Inne niechciane zmienne (NVotes, Leave, Vote i RegionName) zostały usunięte w funkcji get_numerical_variable_ames()na początku części. Następnie otrzymujemy rzeczywiste nazwy zmiennych z wartościami TRUE, dzięki czemu możemy pracować z ciągiem znaków, a nie z wartością logiczną. Następnie obliczamy całkowitą liczbę zmiennych jako n, a rzeczywistą liczbę zmiennych uwzględnimy w kombinacjach, biorąc parametry procentowe, mnożąc je przez liczbę zmiennych i uzyskując dolną lub górną granicę dla tej liczby do upewnij się, że uwzględniamy skrajności. Następnie inicjalizujemy obiekt all_combination, który będzie zawierał listę żądanych kombinacji. Następna część to obiekt paska postępu, którego nie będziemy wyjaśniać, ponieważ używaliśmy go wcześniej. Właściwa praca jest wykonywana wewnątrz pętli for. Zauważ, że przechodzi od minimalnej do maksymalnej liczby zmiennych, które chcemy w naszych kombinacjach. W każdej iteracji obliczamy liczbę kombinacji, które są nam zwracane jako macierz, w której każda kolumna reprezentuje inną kombinację, a każdy wiersz zawiera indeks zmiennych dla tej konkretnej kombinacji. Oznacza to, że musimy dodać każdą z tych kolumn do naszej całkowitej listy kombinacji (all_combination), co robimy wewnątrz zagnieżdżonej pętli for. Wreszcie, ponieważ mamy zagnieżdżone listy, chcemy użyć funkcji unlist(), aby przenieść je na ten sam poziom, ale nie chcemy tego robić rekurencyjnie, ponieważ zakończylibyśmy po prostu jedną długą listą i nie bylibyśmy w stanie odróżnić jednej kombinacji od drugiej. Zachęcam do zmiany instrukcji return, aby uniknąć używania parametru recursive = FALSE, a także w ogóle unikać używania funkcji unlist(). Dzięki temu szybko dowiesz się, jaki wpływ mają one na wyjście funkcji i dlaczego ich potrzebujemy.
library(progress)
generate_combinations_uvectorized <- function(variables, min_percentage, max_percentage){
variables[[„Proportion”]] <- FALSE
variables <- names(variables[variables == TRUE])
n <- length(varibles)
n_min <- floor(n * min_percentage)
n_max <- ceiling(n * max_percentage)
all_combinations <- NULL
progres_bar <- progres_bar$new (
format = „Progress [:bar] :percent ETA: :eta”,
total = length(n_min:n_max)
)
for (k in n_min:n_max) {
progres_bar$tick()
combinations <- combn(variables,k)
for (column i 1:ncol(combinations)) {
new_llist <- list(combiations[, column])
all_combinatinos <- c(all_ombinations , list(new_list_)
}
}
return(unlist(all_ombinations, recursive = FALSE))
Przykładowe dane wyjściowe obiektu, dla którego funkcja generate_combinations_unvectorized() nie jest pokazana obok Jak widać, jest to lista, na której każdy element jest wektorem lub typem character. Pierwsza utworzona kombinacja zawiera tylko 17 zmiennych, co stanowi minimalną liczbę użytych zmiennych, gdy całkowita liczba zmiennych wynosi 19, a minimalny wymagany procent to 90%. Ostatnia kombinacja (numer kombinacji 191) zawiera wszystkie 19 zmiennych i odpowiada modelowi, który zbudowaliśmy ręcznie wcześniej:
combinations <- generate_combinations_unvectorized(
numerical_variables, 0.9, 1.0
)
combiations
[[1]]
[1] „Residents” „Households” „White” „Owned”
[5] „OwnedOutright” „SocialRent” „PrivateRent” „Students”
[9] „Unemp” „UnempRate_EA” „HigherOccup” „Density”
[13] „Deprived” „MultiDepriv” „Age_18to44” „Age_45plus”
[17] „NonWhite”
…
[[191]]
[1] ] „Residents” „Households” „White”
[4] „Owned” „OwnedOutright” „SocialRent”
[7] „PrivateRent” „Students” „Unemp”
[10] „UnempRate_EA” „HigherOccup” „Density”
[13] „Deprived” „MultiDepriv” „Age_18to44”
[16] „Age_45plus” „NonWhite” „HighEducationalLevel”
[19] „LowEducationLevel”
Uzyskanie tylko tych kombinacji, które zawierają od 90% do 100% zmiennych, może wydawać się nieco restrykcyjne. A co jeśli chcemy wygenerować wszystkie możliwe kombinacje? W takim przypadku zmienilibyśmy pierwszy parametr na 0, ale może to nie zakończyć się w praktycznym czasie. Powodem jest to, że nasza funkcja generate_combiations_unvectorized(), jak sama nazwa wskazuje, nie jest wektoryzowany, a co gorsza, ma zagnieżdżone pętle for. W tym konkretnym przypadku jest to ogromne wąskie gardło i jest to coś, na co chcesz zwrócić uwagę we własnym kodzie. Jednym z możliwych rozwiązań jest wykonanie zwektoryzowanej wersji funkcji. W tych przypadkach, w których wektoryzacja i inne podejścia zależne tylko od samego R nie są wystarczająco dobre, możesz spróbować delegować zadanie do szybszego (skompilowanego) języka. Wracając do naszego przykładu, następną rzeczą do zrobienia jest utworzenie funkcji find_best_fit(), która przejdzie przez każdą z wygenerowanych kombinacji, używając danek data_train, aby wytrenować model z odpowiednią kombinacją, przetestuj jego dokładność za pomocą selekcji measure (albo Proportion (numeryczna) albo Vote (kategoryczna) ) i zapisze odpowiedni wynik w wektorze scores. Następnie znajdzie indeks optymalnego wyniku, znajdując minimalny lub maksymalny wynik, w zależności od wyboru measure, którego używamy (Proportion wymaga od nas zminimalizowania podczas gdy Vote wymaga od nas maksymalizacji), a na koniec odtworzy optymalny model, wydrukuje informacje i zwróci model użytkownikowi. Funkcje computer_model_and_fit(), computer_score() i print_best_model)info() zostaną opracowane w następnej kolejności, zgodnie z podejściem odgórnym:
find_best_fit <- fuctio(measure, data_trai, data_test, ombiations) {
n_cases <- length(combinations)
progress_bar <- progress_bar$new(
format = „Progress [:bar] :percent ETA: :eta”,
total = _cases
)
scores <-lapply*1:n_cases, function(i) {
progress_bar$tick()
results <- computer_model_and_fit(combinatios [[i]] , data_train)
score <- computer_sore(measure, results[[„fit”]] , data_test)
return(score)
})
i <- ifelse(measure == „Proprotion” , which.min(scores),
which.max(scores))
best_results <- computer_model_and_fit(combinations [[i]], data_train)
best_score <- computer_score(measure, best_results[[„fit”]], data_test)
print_best_model_info(i, best_results[[„mode”]], best_score, measure)
return(best_results[[„fit”]])
}
Następnie tworzymy funkcję computer_model_and_fit, która po prostu generuje formułę dla wybranej kombinacji i wykorzystuje ją w funkcji lm() Jak widać w obiekcie combiations, poprzednio wróciliśmy z funkcji generate_combiations_unvectorized() , to lista z wektorami znaków, to nie jest formuła my może przejść do funkcji lm(); dlatego potrzebujemy funkcji generate_model(), która przejmie te wektory i połączy jej elementy w jeden ciąg ze znakiem plus (+) między nimi poprzez użycie funkcji paste() z argumentem collapes + „ + „ i doda do niej łańcuch Proportion . To daje nam z powrotem obiekt formuły określony przez łańcuch, taki jak Proprotion ~ Resident + … + NonWhite, który zawiera zamiast kropek wszystkie zmienne w pierwszej kombinacji pokazanej w poprzednim kodzie. Ten ciąg jest następnie używany wewnątrz funkcji lm() do wykonania naszej regresji, a zarówno model, jak ifit są zwracane w ramach listy do użycia w następujących krokach:
cmpute_model_and_fit <- function(cmobination,data_train) {
model <- generate_model(combination)
return (list(model = model , fit = lm(model, data_train)))
}
geerate_model <- function(combination) {
sum <- paste(combinatio, collapse = „ + „ )
return(formula(paste(„Proportion”, „~” , sum)))
}
Jak widać po linii score<- computer_sore(measure, results[[„fit”]], data_test, funkcja computer_score() otrzymuje obiekt measure, obiekt fit (który pochodzi z listy results) oraz dane użyte do testów. Oblicza wynik przy użyciu wspomnianego wcześniej wzorca strategii dla wykresów użytych do sprawdzenia założenia o normalności. Zasadniczo, w zależności od wartości ciągu measure (wybranej strategii), wybierze jedną z dwóch funkcji, które mają ten sam podpis, i ta funkcja zostanie użyta do obliczenia ostatecznych prognoz. Wysyłamy parametr se.fit = TRUE do funkcji predict(), którą widzieliśmy wcześniej, ponieważ chcemy, aby standardowe błędy były również wysyłane w przypadku, gdy używamy wyniku liczbowego co ich wymaga. Funkcje score_proprotions() i score_votes() zostały zdefiniowane wcześniej :
compute_score <- function(measure, fit , data_test) {
if (measure = = „Proprotion”) {
score <- score_proprotions
}else {
score <- score_votes
}
predictions <- predict(fit, data_test, se,fit = TRUE_
return(score(data_test, prediction))
}
Na koniec tworzymy małą wygodną funkcję o nazwie print_best_model_info(), która wypisze wyniki dotyczące najlepszego znalezionego modelu. Po prostu pobiera indeks najlepszego modelu, formułę modelu, jego wynik oraz typ miary i drukuje to wszystko dla użytkownika. Jak widać, ponieważ obiekt model nie jest prostym ciągiem, ale obiektem formuły, musimy trochę popracować z nim, aby uzyskać pożądane wyniki, konwertując go na ciąg i dzieląc za pomocą znaku plus (+) wiemy, że jest uwzględniony; w przeciwnym razie byłby to bardzo długi ciąg:
print_best_model_ifo <- function(i, model, best_score, measure) {
print („ **************************************************”)
print(paste(„Best model number: „ , i))
print(paste(„Best score: „, best_score))
print(paste(„Score measure : „ , measure))
print(„Best model: „)
print(strsplit(toString(model), „\\+:))\
print („ **************************************************”)
Możemy znaleźć najlepszy model, zgodnie z miarą Proportion, wywołując:
best_lm_fit_by_proprotions <- find_best_fit(
measure = „Proprotion”,
data_train = data_train,
data_test = data_test,
combinatios = combinations
)
#> [1] “*************************************”
#> [1] “Best model number: 3”
#> [1] “Best score: 10.2362983528259”
#> [1] “Score measure: Proportion”
#> [1] “Best model:”
#> [[1]]
#> [1] “~, Proportion, Residents ” ” Households “
#> [3] ” White ” ” Owned “
#> [5] ” OwnedOutright ” ” SocialRent “
#> [7] ” PrivateRent ” ” Students “
#> [9] ” Unemp ” ” UnempRate_EA “
#> [11] ” HigherOccup ” ” Density “
#> [13] ” Deprived ” ” MultiDepriv “
#> [15] ” Age_18to44 ” ” Age_45plus “
#> [17] ” LowEducationLevel”
#> [1] “*************************************”
Jak widać, najlepszym modelem był trzeci ze 191 modeli z notą 10,23. Możemy również zobaczyć regresory użyte w modelu. Jak widać, NoWhite i HighEducationLevel zostały pominięte w metodzie optymalizacji, prawdopodobnie ze względu na ich odpowiedniki zawierające wszystkie niezbędne informacje dla odpowiednich grup. To nie przypadek, że są to jedne z najbardziej reprezentatywnych zmiennych w danych. Aby znaleźć najlepszy model według miary Vote, używamy następującego kodu. Zauważ, że biorąc pod uwagę dobre techniki, których użyliśmy do stworzenia tej funkcji, wszystko, co musimy zrobić, to zmienić wartość parametru measure, aby zoptymalizować nasze wyszukiwanie przy użyciu innego podejścia:
best_lm_fit_by_votes <- find_best_fit (
measure = „Vote”
data_train = data_train,
data_test = data_test
ombinations = combinations
)
#> [1] “*************************************”
#> [1] “Best model number: 7”
#> [1] “Best score: 220”
#> [1] “Score measure: Vote”
#> [1] “Best model:”
#> [[1]]
#> [1] “~, Proportion, Residents ” ” Households “
#> [3] ” White ” ” Owned “
#> [5] ” OwnedOutright ” ” SocialRent “
#> [7] ” PrivateRent ” ” Students “
#> [9] ” Unemp ” ” UnempRate_EA “
#> [11] ” HigherOccup ” ” Density “
#> [13] ” Deprived ” ” MultiDepriv “
#> [15] ” Age_45plus ” ” NonWhite “104
#> [17] ” HighEducationLevel”
#> [1] “*************************************”
W tym przypadku najlepszym modelem był siódmy ze 191 modeli, z 220 z 241 poprawnych prognoz, co daje nam dokładność 91%, co jest poprawą, biorąc pod uwagę dokładność obliczoną wcześniej w tym rozdziale. W tym przypadku LowEducationLevel i Age_18to44 zostały pominięte. Ponownie, nie jest przypadkiem, że są to jedne z najważniejszych zmiennych w danych.