Nasz pierwszy wykres jest prosty i pokazuje proporcje głosów dla każdej nazwy regionu. Jak widać na poniższym wykresie, regiony Londynu, północno-zachodniego i zachodniego Midlands stanowią około 55 procent obserwacji w danych.
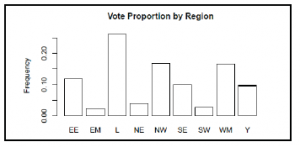
Aby stworzyć wykres, musimy stworzyć tabelę dla częstotliwości każdego regionu w RegionName z funkcją table (), a następnie podać ją do funkcji prop.table (), która oblicza odpowiednie proporcje, które z kolei są używane jako wysokości dla każdego paska.
Używamy funkcji barplot () do tworzenia wykresu i możemy określić niektóre opcje, takie jak tytuł (główna), etykieta osi y (ylab) i kolor słupków col). Jak zawsze, możesz dowiedzieć się więcej o parametrach funkcji za pomocą ? barplot
tabela (dane $ RegionName)
#> EE EM L NE NW SE SW WM Y
#> 94 20210 32 134 79 23133 78
prop.table (table (data $ RegionName))
#> EE EM L NE NW SE SW WM Y
#> 0,11706 0,02491 0,26152 0,03985 0,16687 0,09838 0,02864 0,16563 0,09714
barplot (
wysokość = prop.table (table (data $ RegionName)),
main = “Proporcja głosów według regionu”,
ylab = “Częstotliwość”,
col = “biały”
)
Nasz kolejny wątek, pokazany poniżej, jest nieco bardziej przyciągający wzrok. Każdy punkt reprezentuje obserwację totemu i pokazuje proporcję głosów opuszczonych dla każdego totemu, ułożonych w pionowe linie odpowiadające RegionName i pokolorowane według proporcji białej populacji dla każdego okręgu. Jak widać, mamy kolejne interesujące odkrycie; wydaje się, że im bardziej zróżnicowana jest populacja podopiecznego (co widać po ciemniejszych punktach), tym większe jest prawdopodobieństwo, że podopieczny opowie się za pozostaniem w UE (niższa wartość proporcji).
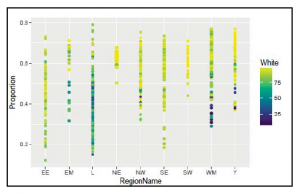
Aby stworzyć wykres, musimy załadować pakiety ggplot2 i virdis; pierwszy z nich posłuży do stworzenia faktycznego wykresu, a drugi posłuży do pokolorowania punktów za pomocą interesującej naukowo palety kolorów zwanej Viridis (pochodzi z badań percepcji kolorów przeprowadzonych przez Nathaniela Smitha i Stfana van der Walta). Na razie wszystko, co musisz wiedzieć, to to, że funkcja otrzymuje jako pierwszym parametrem jest ramka danych z danymi, które będą użyte na wykresie, a jako drugi parametr obiekt estetyki (aes), utworzony funkcją aes(), która z kolei może otrzymać parametry dla zmiennej, która należy używać na osi x, osi y i kolorze. Następnie dodajemy warstwę punktów z funkcją geom_points(), a paletę kolorów Viridis funkcją scale_olor_viridis() . Zwróć uwagę, jak dodajemy obiekty wykresu podczas pracy z ggplot2. Jest to bardzo wygodna funkcja, która zapewnia dużą moc i elastyczność. Na koniec pokazujemy wykres z funkcją print() (w R niektóre funkcje używane do kreślenia natychmiast pokazują wykres (na przykład barplot), podczas gdy inne zwracają obiekt wykresu (dla przykład, ggplot2) i należy je jawnie wydrukować):
library(ggplot2)
library(viridis)
plot <- ggplot(data, aes(x = RegionName, y = Proportion, color = White))
plot <- plot + geom_point() + scale_color_viridis()
print(plot)
Następny zestaw wykresów, pokazany poniżej, wyświetla histogramy dla zmiennych NoQuals, L4Quals_plus i AdltMeanAge. Jak widać, zmienna NoQuals wydaje się mieć rozkład normalny, ale zmienne L4Quals_plus i AdultMeanAge wydają się mieć być pochylony odpowiednio w lewo i w prawo. To mówi nam, że większość osób w próbie nie ma wyższego poziomu wykształcenia i ma ponad 45 lat.

Tworzenie tych wykresów jest dość proste; wystarczy przekazać zmienną, która będzie używana w histogramie, do funkcji hist () i opcjonalnie określić tytuł i etykietę osi x dla wykresów (które zostawiamy puste, ponieważ informacje są już w tytule wykresu). Spójrzmy na następujący kod:
hist(data$NoQuals, main = „Histogram for NoQuals”, xlab = „ „)
hist(data$L4Quals, main = „Histogram for L4Quals_plus”, xlab = „ „)
hist(data$AdyltMeanAge, main = „Histogram for AdultMeanAge”, xlab = „ „)
Teraz, gdy rozumiemy nieco więcej na temat dystrybucji zmiennych NoQuals, L4Quals_plus i AdultMeanAge, zrozumiemy zobacz ich wspólny rozkład na wykresach punktowych pokazanych poniżej. Możemy zobaczyć, jak te wykresy rozrzutu przypominają histogramy, porównując oś x i oś y na wykresach rozrzutu z odpowiednią osią x na histogramach i porównując częstotliwość (wysokość) na histogramach z gęstością punktów na wykresach rozrzutu.
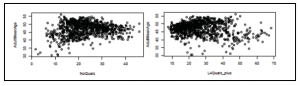
Znajdujemy niewielką zależność, która pokazuje, że im starsi ludzie, tym niższy poziom wykształcenia. Można to interpretować na wiele sposobów, ale zostawimy to jako ćwiczenie, aby skupić się na programowaniu, a nie na statystykach. Tworzenie tych wykresów punktowych to również bardzo proste. Po prostu wyślij zmienne x i y do funkcji plot()i opcjonalnie określ etykiety dla osi.
plot(x = data$NoQuals, y = data$AdultMeanAge, ylab = „AdultMeanAge”, xlab = „NoQuals”)
plot(x = data$L4Quals_plus, y = data$AdultMeanAge, ylab = „AdultMeanAge”, xlab = „L4Quals_plus”)