Miesiąc: październik 2020

Nasz pierwszy wykres jest prosty i pokazuje proporcje głosów dla każdej nazwy regionu. Jak widać na poniższym wykresie, regiony Londynu, północno-zachodniego i zachodniego Midlands stanowią około 55 procent obserwacji w danych.

Aby stworzyć wykres, musimy stworzyć tabelę dla częstotliwości każdego regionu w RegionName z funkcją table (), a następnie podać ją do funkcji prop.table (), która oblicza odpowiednie proporcje, które z kolei są używane jako wysokości dla każdego paska.

Używamy funkcji barplot () do tworzenia wykresu i możemy określić niektóre opcje, takie jak tytuł (główna), etykieta osi y (ylab) i kolor słupków col). Jak zawsze, możesz dowiedzieć się więcej o parametrach funkcji za pomocą ? barplot

tabela (dane $ RegionName)

#> EE EM L NE NW SE SW WM Y

#> 94 20210 32 134 79 23133 78

prop.table (table (data $ RegionName))

#> EE EM L NE NW SE SW WM Y

#> 0,11706 0,02491 0,26152 0,03985 0,16687 0,09838 0,02864 0,16563 0,09714

barplot (

wysokość = prop.table (table (data $ RegionName)),

main = “Proporcja głosów według regionu”,

ylab = “Częstotliwość”,

col = “biały”

)

Nasz kolejny wątek, pokazany poniżej, jest nieco bardziej przyciągający wzrok. Każdy punkt reprezentuje obserwację totemu i pokazuje proporcję głosów opuszczonych dla każdego totemu, ułożonych w pionowe linie odpowiadające RegionName i pokolorowane według proporcji białej populacji dla każdego okręgu. Jak widać, mamy kolejne interesujące odkrycie; wydaje się, że im bardziej zróżnicowana jest populacja podopiecznego (co widać po ciemniejszych punktach), tym większe jest prawdopodobieństwo, że podopieczny opowie się za pozostaniem w UE (niższa wartość proporcji).

Aby stworzyć wykres, musimy załadować pakiety ggplot2 i virdis; pierwszy z nich posłuży do stworzenia faktycznego wykresu, a drugi posłuży do pokolorowania punktów za pomocą interesującej naukowo palety kolorów zwanej Viridis (pochodzi z badań percepcji kolorów przeprowadzonych przez Nathaniela Smitha i St􀁤fana van der Walta). Na razie wszystko, co musisz wiedzieć, to to, że funkcja otrzymuje jako pierwszym parametrem jest ramka danych z danymi, które będą użyte na wykresie, a jako drugi parametr obiekt estetyki (aes), utworzony funkcją aes(), która z kolei może otrzymać parametry dla zmiennej, która należy używać na osi x, osi y i kolorze. Następnie dodajemy warstwę punktów z funkcją geom_points(), a paletę kolorów Viridis funkcją scale_olor_viridis() . Zwróć uwagę, jak dodajemy obiekty wykresu podczas pracy z ggplot2. Jest to bardzo wygodna funkcja, która zapewnia dużą moc i elastyczność. Na koniec pokazujemy wykres z funkcją print() (w R niektóre funkcje używane do kreślenia natychmiast pokazują wykres (na przykład barplot), podczas gdy inne zwracają obiekt wykresu (dla przykład, ggplot2) i należy je jawnie wydrukować):

library(ggplot2)

library(viridis)

plot <- ggplot(data, aes(x = RegionName, y = Proportion, color = White))

plot <- plot + geom_point() + scale_color_viridis()

print(plot)

Następny zestaw wykresów, pokazany poniżej, wyświetla histogramy dla zmiennych NoQuals, L4Quals_plus i AdltMeanAge. Jak widać, zmienna NoQuals wydaje się mieć rozkład normalny, ale zmienne L4Quals_plus i AdultMeanAge wydają się mieć być pochylony odpowiednio w lewo i w prawo. To mówi nam, że większość osób w próbie nie ma wyższego poziomu wykształcenia i ma ponad 45 lat.

Tworzenie tych wykresów jest dość proste; wystarczy przekazać zmienną, która będzie używana w histogramie, do funkcji hist () i opcjonalnie określić tytuł i etykietę osi x dla wykresów (które zostawiamy puste, ponieważ informacje są już w tytule wykresu). Spójrzmy na następujący kod:

hist(data$NoQuals, main = „Histogram for NoQuals”, xlab = „ „)

hist(data$L4Quals, main = „Histogram for L4Quals_plus”, xlab = „ „)

hist(data$AdyltMeanAge, main = „Histogram for AdultMeanAge”, xlab = „ „)

Teraz, gdy rozumiemy nieco więcej na temat dystrybucji zmiennych NoQuals, L4Quals_plus i AdultMeanAge, zrozumiemy zobacz ich wspólny rozkład na wykresach punktowych pokazanych poniżej. Możemy zobaczyć, jak te wykresy rozrzutu przypominają histogramy, porównując oś x i oś y na wykresach rozrzutu z odpowiednią osią x na histogramach i porównując częstotliwość (wysokość) na histogramach z gęstością punktów na wykresach rozrzutu.

Znajdujemy niewielką zależność, która pokazuje, że im starsi ludzie, tym niższy poziom wykształcenia. Można to interpretować na wiele sposobów, ale zostawimy to jako ćwiczenie, aby skupić się na programowaniu, a nie na statystykach. Tworzenie tych wykresów punktowych to również bardzo proste. Po prostu wyślij zmienne x i y do funkcji plot()i opcjonalnie określ etykiety dla osi.

plot(x = data$NoQuals, y = data$AdultMeanAge, ylab = „AdultMeanAge”, xlab = „NoQuals”)

plot(x = data$L4Quals_plus, y = data$AdultMeanAge, ylab = „AdultMeanAge”, xlab = „L4Quals_plus”)

Teraz, gdy mamy już kilka czystych danych do pracy, utworzymy wiele wykresów, aby zbudować intuicję dotyczącą danych. Tu będziemy pracować z wykresami, które są łatwe do utworzenia i służą do celów eksploracyjnych. Później przyjrzymy się gotowym do publikacji wykresom, które są nieco bardziej szczegółowe

 

Aby uzyskać podsumowanie danych, możemy wykonać summary(data) i zobaczyć odpowiednie podsumowania dla każdego typu zmiennej. Podsumowanie jest dostosowane do typu danych każdej kolumny. Jak widać, zmienne liczbowe, takie jak ID i NVotes, uzyskują podsumowanie kwantylowe, podczas gdy zmienne czynnikowe (kategorialne) uzyskują liczbę dla każdej kategorii, na przykład AreaType i RegionName. Jeśli istnieje wiele kategorii, podsumowanie pokaże kategorie, które pojawiają się najczęściej, a resztę zgrupuje w (Other) grupę, jak widać na dole RegionName.

summary(date)

#> ID RegionName NVotes Opuść

#> Min. : 1 Długość: 1070 min. : 1039 min. : 287

#> 1. kw .: 268 Klasa: znak 1. kw .: 4252 1. kw .: 1698

#> Mediana: 536 Tryb: znak Mediana: 5746 Mediana: 2874

#> Średnia: 536 Średnia: 5703 Średnia: 2971

#> 3

#> Max. : 1070 Maks. : 15148 Maks. : 8316

(Obcięte wyjście)

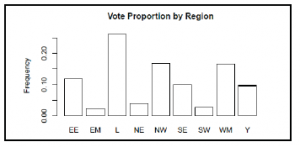
Stąd widać, że Londyn jest regionem, do którego należy więcej okręgów, a następnie północno-zachodnia i zachodnia część Midlands. Widzimy również, że podopieczny z najmniejszą liczbą głosów we wszystkich danych miał tylko 1039 głosów, ten z największą liczbą głosów – 15 148, a średnia liczba głosów na podopiecznego wyniosła 5703. W dalszej części rozdziału przyjrzymy się dokładniej tego rodzaju analizom. Na razie skupimy się na tym, aby podsumowanie danych było przydatne do dalszej analizy. Jak być może zauważyłeś, nie możemy używać wyników summary() do wykonywania obliczeń. Możemy spróbować zapisać podsumowanie w zmiennej, poznać typ zmiennej i przejść przez nią w odpowiedni sposób. Jeśli jednak to zrobimy, okaże się, że są to dane tekstowe, co oznacza, że ​​nie możemy ich użyć do obliczeń, tak jak jest:

summary <- summary(data)

class(summary)

#> [1] “tabela”

summary[1]

#> [1] “Min.: 1”

class (summary[1])

#> [1] “znak”

Z pewnością musi istnieć sposób na umieszczenie danych summary w ramce danych w celu dalszej analizy. To jest R, więc możesz się założyć, że jest! Pierwszą rzeczą, na którą powinniśmy zwrócić uwagę, jest to, że nie możemy bezpośrednio przetłumaczyć wyjścia funkcji summary() na ramkę danych ze względu na zmienne nieliczbowe. Te zmienne nienumeryczne zawierają inną strukturę podsumowującą, która nie składa się z wartości minimalnych, pierwszego kwartylu, mediany, średniej, trzeciego kwartylu i maksymalnych. Oznacza to, że najpierw musimy podzielić dane, aby uzyskać tylko dane liczbowe zmienne. W końcu ramka danych jest prostokątną strukturą z dobrze zdefiniowanymi wierszami i kolumnami. Gdybyśmy próbowali mieszać typy (włączając podsumowania liczbowe i nieliczbowe) w ramce danych, byłoby to trudne. Aby sprawdzić, czy kolumna jest liczbowa, czy nie, możemy użyć funkcji is.numeric(). Na przykład widzimy, że kolumna Proportion jest numeryczna, a RegionName nie jest:

is.numeric(data$Proportion)

#> [1] TRUE

is.numeric(data$RegioName)

#> [1] FALSE

Następnie możemy zastosować is.numeric() do każdej kolumny za pomocą funkcji sapply(). To da nam wektor logiczny (boolowski) z wartością TRUE lub FALSE dla każdej kolumny, wskazującą, czy jest to liczba. Następnie możemy użyć tego wektora logicznego do podzbioru naszych danych i pobierz tylko kolumny liczbowe z datat[, numerical_varaibles]. Jak widzisz, w obiekcie data_numerical nie ma kolumn nienumerycznych:

numerical_variables <- sapply(data, is.numeric)

numerical_variables

#> ID RegionName NVotes Leave Residents

#> TRUE FALSE TRRUE TRUE TRUE

#> Households MeanAge AdultMeanAge Aget_0to4 Age_5to7

#> TRUE TRUE TRUE TRUE TRUE

data_numerical <- datat[, numerical_variables]

colnames(data_numerical)

#> [1] “ID” “Nvotes” “Leave” “Residents”

#> [5] “Households” “MeanAge” “AdultMeanAge” “Age_0to4”

#> [9] “Age_5to7” “Age_8to9” “Age_10to14” “Age_15”

#> [13] “Age_16to17 “Age_18to19” “Age_20to24” “Age_25to29”

(Obcięte dane wyjściowe)

Ponieważ nie ma sensu uzyskiwanie wartości summary dla zmiennej ID, możemy usunąć ją z wektora logicznego, traktując ją skutecznie jako zmienną nienumeryczną. Jeśli to zrobimy, musimy pamiętać o odtworzeniu obiektu data_numeric, aby upewnić się, że nie zawiera on również zmiennej ID:

numerical_variable[[„ID”]] <- FALSE

data_numerical <- data [, numerical_variables]

Aby utworzyć podsumowanie zmiennych numerycznych, najpierw zastosujemy funkcję summary(), którą utworzyliśmy wcześniej, do każdej kolumny liczbowej za pomocą funkcji lapply(). Funkcja lapply() zwraca nazwaną listę, gdzie każdy element listy ma odpowiednią nazwę kolumny: lapply(data[,numerical_variables], summary)

#> $NVotes

#> Min. 1st Qu. Median Mean 3rd Qu. Max.

#> 1039 4252 5746 5703 7020 15148

#>

#> $Leave

#> Min. 1st Qu. Median Mean 3rd Qu. Max.

#> 287 1698 2874 2971 3936 8316

#>

#> $Residents

#> Min. 1st Qu. Median Mean 3rd Qu. Max.

#> 1932 8288 11876 11646 14144 34098

#>#>

(Obcięte wyjście)

Teraz musimy umieścić każdego członka tej listy razem w ramce danych. W tym celu użyjemy funkcji cbind() i do.call(). do.call() będą obowiązywać kolejno cbind() do każdego członka listy wygenerowanej przez lapply() i zwróć je wszystkie razem.

numerical_summary <- do.call(cbid, lapply(data_numerical, summary))

#> Warning in (function (…, deparse.level = 1) : number of rows of result

is

#> not a multiple of vector length (arg 1)

numerical_summary

#> NVotes Leave Residents Households MeanAge AdultMeanAge Age_0to4

#> Min. 1039 287 1932 779 27.80 29.20 2.200

#> 1st Qu. 4252 1698 8288 3466 35.60 44.10 5.400

#> Median 5746 2874 11876 4938 38.70 47.40 6.300

#> Mean 5703 2971 11646 4767 38.45 46.85 6.481

#> 3rd Qu. 7020 3936 14144 5832 41.40 49.90 7.50058

#> Max. 15148 8316 34098 15726 51.60 58.10 12.300

#> NA’s 1039 267 1932 779 27.80 29.20 2.200

Otrzymaliśmy nasze wyniki, ale nie tak szybko! Dostaliśmy ostrzeżenie i wygląda to podejrzanie. Co oznacza wiadomość number of rows of result is not a multiple of vector legth oznacza wiadomość? Aha! Jeśli przyjrzymy się dokładniej liście, którą otrzymaliśmy wcześniej z naszego lapply() widzimy, że w przypadku Leave  (i Proportion) otrzymujemy dodatkową kolumnę dla NAs, której nie otrzymujemy dla żadnej innej kolumny. Oznacza to, że kiedy spróbujemy użyć cbind() na tych kolumnach, dodatkowa kolumna NAs utworzy dodatkową przestrzeń, którą należy wypełnić. Jak widzieliśmy, R radzi sobie z tym, powtarzając wektory po kolei, aż wszystkie przestrzenie zostaną wypełnione. W naszym przypadku oznacza to, że pierwszy element, odpowiadający wartości minimalnej, zostanie powtórzony dla przestrzeni NA dla każdej kolumny, która nie ma spacji NA. Możesz to sprawdzić, porównując liczby w kolumnach Min i NAs dla zmiennych innych niż Leave lub Proportion (dla tych dwóch wartości powinny być faktycznie różne) . Aby to naprawić, możemy po prostu usunąć wiersz dodatkowej wartości NA z wynikowej ramki danych, ale to nie dotyczy źródła ostrzeżenia, a jedynie objaw. Aby poradzić sobie ze źródłem, musimy mieć taką samą liczbę kolumn dla każdej zmiennej, zanim zastosujemy cbind(). Ponieważ już wiemy, że mamy 267 braków danych dla zmiennej Leave, które wtedy wpływają na zmienną Proportion, możemy to łatwo naprawić, ignorując te informacje. Aby to zrobić, po prostu używamy pełnych przypadków, co oznacza, że ​​przechowujemy obserwacje, które nie mają żadnych wartości NA w żadnej ze swoich zmiennych; lub inaczej mówiąc, pomijamy każdą obserwację, która zawiera co najmniej jeden 􀀯􀀢. Gdy to zrobimy, odzyskamy wyniki i nie otrzymujemy żadnych ostrzeżeń:

data <- data[complete.cases(data), ]

data_numerical <- data[, numerical_variables]

numerical_summary <- do.call(cbind, lapply(data_numerical, summary))

numerical_summry

#> NVotes Leave Residents Households MeanAge AdultMeanAge Age_0to4

#> Min. 1039 287 1932 779 28.40 30.50 2.200

#> 1st Qu. 4242 1698 8405 3486 35.70 44.10 5.400

#> Median 5739 2874 11911 4935 38.60 47.40 6.300

#> Mean 5725 2971 11739 4793 38.43 46.83 6.479

#> 3rd Qu. 7030 3936 14200 5850 41.40 49.90 7.500

#> Max. 15148 8316 34098 15726 47.30 56.10 12.300

(Obcięte wyjście)

Jeśli chcemy otrzymać wartości podsumowania jako kolumny, a zmienne jako wiersze, możemy użyć funkcji rbind() zamiast cbind(). Struktura, której faktycznie używamy, będzie zależeć od tego, co chcemy z nią zrobić. Możemy jednak łatwo przełączać się między nimi później, jeśli zajdzie potrzeba:

do.call(rbind, lapply(data_numerical, summary))

#> Min. 1st Qu. Median Mean 3rd Qu.

Max.

#> NVotes 1039.0000 4241.5000 5.739e+03 5.725e+03 7.030e+03

1.515e+04

#> Leave 287.0000 1697.5000 2.874e+03 2.971e+03 3.936e+03

8.316e+03

#> Residents 1932.0000 8405.0000 1.191e+04 1.174e+04 1.420e+04

3.410e+04

#> Households 779.0000 3486.0000 4.935e+03 4.793e+03 5.850e+03

1.573e+04

#> MeanAge 28.4000 35.7000 3.860e+01 3.843e+01 4.140e+01

4.730e+01

Teraz, gdy mamy ten obiekt numerical_summary możemy go użyć do wykonania obliczeń, takich jak znalezienie zakresu między totemami z najmniejszą i największą liczbą głosów za opuszczenia szkoły (0,6681), co może być przydatne do interpretacji dużej różnicy między typami oddziałów, jakie możemy znaleźć w Wielkiej Brytanii. Jeśli chcemy wiedzieć, które totemy są używane, aby dostać się do tego wyniku, możemy wyszukać totemy z najmniejszą i największą liczbą głosów:

numericla_summary[„Max.”, „Proportion”] – numerical_summary[„Min.”, „Proportion”

desired_variables <- c(

„ID”,

„NoQuals”,

„Proportion”,

„AdultMeanAge”,

„L4Quals_plus”,

„RegionName”

)

>data[which.max(data$Proportion), desired_variables]

#> ID NoQuals Proportion AdultMeanAge L4Quals_plus RegionName

#> 754 754 35.8 0.7897 48.7 13.7 L

data[which.min(data$Proportion), desired_variables]

#> ID NoQuals Proportion AdultMeanAge L4Quals_plus RegionName

#> 732 732 2.8 0.1216 31.2 44.3 EE

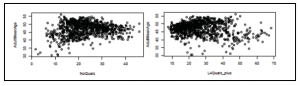
Jak widać, ta analiza już pokazuje interesujące wyniki. Okręg w Wielkiej Brytanii, który głosował za opuszczeniem UE najbardziej, charakteryzuje się osobami starszymi (MeanAge) z niskim poziomem wykształcenia (oQuals, L4Quals-plus). Z drugiej strony oddział Wielkiej Brytanii, który głosował za pozostaniem w UE najbardziej, charakteryzuje się młodymi ludźmi z dużo wyższym wykształceniem. Oczywiście nie jest to pełny obraz, ale jest to wskazówka dotycząca kierunku, w którym musimy spojrzeć, aby lepiej zrozumieć, co się dzieje. Na razie stwierdziliśmy, że wykształcenie i wiek wydają się być istotnymi zmiennymi do analizy

Konfiguracja danych dla tego przykładu jest prosta. Załadujemy dane, poprawnie oznaczymy brakujące wartości i utworzymy nowe zmienne do naszej analizy. Zanim zaczniemy, upewnij się, że plik data.csv znajduje się w tym samym katalogu, co kod, z którym pracujesz, i że twój katalog roboczy jest poprawnie skonfigurowany. Jeśli nie wiesz jak to zrobić, skonfigurowanie katalogu roboczego jest dość łatwe, po prostu wywołaj funkcję setwd() przekazującą katalog chcesz użyć jako takiego. Na przykład setwd(/home/user/examples użyje katalogu /home/users/examples  do wyszukiwania plików i zapisywania plików.

Możemy załadować zawartość pliku data.csv do ramki danych (najbardziej intuicyjna struktura do wykorzystania z danymi w formacie CSV) za pomocą funkcji read.csv. Zwróć uwagę, że dane mają pewne braki w zmiennej Leave. Te wartości mają wartość -1, aby je zidentyfikować. Jednak właściwym sposobem identyfikacji brakujących wartości w R jest NA, którego używamy do zastępowania wartości -1.

data <- read.csv(„./data+brexit_referendum.csv”)

data[daa$Leave == -1, „Leave”] <- NA

Aby policzyć liczbę brakujących wartości w naszych danych, możemy użyć funkcji is.na(), aby uzyskać wektor logiczny (boolowski) zawierający TRUE wartości w celu zidentyfikowania brakujących wartości i FALSE wartości do zidentyfikować wartości bez braków danych. Długość takiego wektora będzie równa długości wektora używanego jako wejście, którym w naszym przypadku jest zmienna Leave. Następnie możemy użyć tego wektora logicznego jako danych wejściowych dla sum(), jednocześnie wykorzystując sposób, w jaki R traktuje takie wartości TRUE/FALSE aby uzyskać liczbę brakujących wartości. TRUE jest traktowane jako 1, podczas gdy FALSE jest traktowane jako 0. Okazuje się, że liczba brakujących wartości w zmiennej Leave wynosi 267.

sum(is.na(data$Leave)

#> [1] 267

Jeśli chcemy, możemy użyć mechanizmu do uzupełnienia brakujących wartości. Powszechnym i prostym mechanizmem jest przypisanie średniej zmiennej. Na razie zachowamy prostotę i zostawimy je jako brakujące wartości. Przechodzimy teraz do zdefiniowania nowej zmiennej Proportion, która będzie zawierała procent głosów za opuszczeniem UE. W tym celu dla każdego podopiecznego dzielimy zmienną Leave (liczba głosów za odejściem) przez zmienną NVotes (łączna liczba głosów). Biorąc pod uwagę zwektoryzowany charakter R, jest to proste:

data$Proportion <- data$Leave / data$NVotes

Tworzymy nową zmienną w ramce danych, po prostu ją przypisując. Nie ma różnicy między utworzeniem nowej zmiennej a modyfikacją istniejącej, co oznacza, że ​​musimy zachować ostrożność, aby upewnić się, że przypadkowo nie nadpisujemy starej zmiennej. Teraz utwórz nową zmienną, która zawiera klasyfikację tego, czy większość wychowanków głosowała za opuszczeniem UE, czy też pozostaniem w UE. Jeśli więcej niż 50 procent głosów każdego z podopiecznych było za opuszczeniem, wówczas oznaczymy go jako głosującego za opuszczeniem i odwrotnie. Ponownie, R czyni to bardzo prostym za pomocą funkcji ifelse(). Jeśli wspomniany warunek (pierwszy parametr) jest spełniony, to przypisaną wartością będzie „Leave” (drugi parametr); w przeciwnym razie „Remain” (trzeci parametr). Jest to operacja zwektoryzowana, więc zostanie wykonana dla każdej obserwacji w ramce danych:

data$Vote <- ifelse(data$Proportion > 0.5, „Leave”, „Remain”)

Czasami ludzie lubią używać innej składni dla tego typu operacji; będą używać metody przypisywania podzbiorów, która różni się nieco od tego, którego używaliśmy. Nie będziemy wchodzić w szczegóły różnic między tymi podejściami, ale pamiętaj, że to drugie podejście może spowodować błąd w naszym przypadku:

data[data$Proportion > 0.5 , „Vote”] <- „Leave”

data[data$Proportion <= 0.5 , „Vote”] <- „Remain”

#> Error in `[<-.data.frame`(`*tmp*`, data$Proportion 0.5, “Vote”, value =

“Leave”):

#> missing values are not allowed in subscripted assignments of data frames

Dzieje się tak, ponieważ zmienna Proportion zawiera pewne braki wartości, które były konsekwencją tego, że zmienna Leave ma jakieś NA wartości na pierwszym miejscu. Ponieważ nie możemy obliczyć wartości Proportiondla obserwacji z NA wartościami w Leave, kiedy ją tworzymy, odpowiadające im wartości również otrzymują przypisaną wartość NA.

Jeśli upieramy się przy użyciu metody przypisywania podzbiorów, możemy sprawić, że zadziała, używając funkcji which(). Zignoruje (zwracając jako FALSE) te wartości, które zawierają NA w porównaniu. W ten sposób nie da nam to błędu i uzyskamy taki sam wynik, jak użycie funkcji ifelse(). Powinniśmy używać funkcji ifelse(), gdy jest to możliwe, ponieważ jest prostsza, łatwiejsza do odczytania i wydajniejsza

.

data[which(data$Proportion > 0.5) , „Vote”] <- „Leave”

data[which(data$Proportion <= 0.5) , „Vote”] <- „Remain”

W przyszłości będziemy chcieli stworzyć wykresy zawierające informacje RegionName, a posiadanie długich nazw najprawdopodobniej utrudni ich odczytanie. Aby to naprawić, możemy skrócić te nazwy, gdy jesteśmy w trakcie czyszczenia danych.

data$RegionName <- as.character(data$RegionName)

data[data$RegionName == „London” , „RegionName”]   <- „L”

data[data$RegionName == „North West” , „RegionName”]   <- „NW”

data[data$RegionName == „North East” , „RegionName”]   <- „NE”

data[data$RegionName == „South West” , „RegionName”]   <-„SW”

data[data$RegionName == „South East” , „RegionName”]   <- „SE”

data[data$RegionName == „East Midlands” , „RegionName”]   <-„EM”

data[data$RegionName == „West Midlands” , „RegionName”]   <- „WM”

data[data$RegionName == „East England” , „RegionName”]   <- „EE”

data[data$RegionName == „Yorkshire and The Humber” , „RegionName”]   <-„Y”

Zauważ, że pierwsza linia w poprzednim bloku kodu przypisuje transformację znaku RegionName w typ znaku. Zanim to zrobimy, typem zmiennej jest współczynnik (który pochodzi z domyślnego sposobu odczytu danych za pomocą read.cvs) i uniemożliwia nam to przypisanie innej wartości niż te już zawarte w zmiennej. W takim przypadku otrzymamy błąd, Invalid factor level, NA  generated. Aby uniknąć tego problemu, trzeba wykonać transformację typu. Mamy teraz czyste dane gotowe do analizy. Stworzyliśmy nową interesującą zmienną dla nas (Proportion), na czym skupimy się w pozostałej części ,ponieważ w tym przykładzie jesteśmy zainteresowani ustaleniem relacji między innymi zmiennymi i tym, jak ludzie głosował w referendum.

Tu pokazujemy, jak przeprowadzić opisową analizę statystyczną, aby uzyskać ogólne pojęcie o danych, z którymi mamy do czynienia, co jest zwykle pierwszym krokiem w projektach analizy danych i jest podstawową umiejętnością dla analityków danych w ogóle. Dowiemy się, jak czyścić i przekształcać dane, podsumowywać dane w użyteczny sposób, znajdować konkretne obserwacje, tworzyć różnego rodzaju wykresy zapewniające intuicję dla danych, wykorzystywać korelacje do zrozumienia relacji między zmiennymi numerycznymi, używać głównych składowych do znajdowania optymalnych kombinacji zmiennych , i ułóż wszystko razem w kodzie, który jest wielokrotnego użytku, zrozumiały i łatwy do modyfikacji. Ponieważ jest to tekst programowaniu w R, a nie o robieniu statystyk w R, skupimy się na programowalej stronie rzeczy, a nie na statystycznej stronie. Miej to w pamięci podczas czytania. Niektóre z ważnych tematów omawianych w tym rozdziale są następujące:

* Czyszczenie, przekształcanie i operowanie na danych

* Programowe tworzenie różnego rodzaju wykresów

* Wykonywanie analizy jakościowej różnymi narzędziami w języku R

* Tworzenie nowych zmiennych za pomocą analizy głównych składników

* Tworzenie modułowego i elastycznego kodu, z którym łatwo się pracuje

Wymagane pakiety

Będziemy korzystać z następujących pakietów języka R.

ggplot2: wysokiej jakości wykresy

viridis: Paleta kolorów dla wykresów

corrplot: wykresy korelacji

ggbiplot: Wykresy głównych składników

progress : Pokaż postęp dla iteracji

Przykład głosów w sprawie Brexitu

W czerwcu 2016 r. W Wielkiej Brytanii odbyło się referendum, w którym zdecydowano, czy pozostać częścią Unii Europejskiej (UE). Udział wzięło 72% zarejestrowanych wyborców, z czego 51,2% zagłosowało za opuszczeniem UE. W lutym 2017 r. Martin Rosenbaum, specjalista ds. wolności informacji w BBC News, opublikował artykuł zatytułowany „Liczby głosowania lokalnego rzucają nowe światło na referendum w UE”. Otrzymał dane od 1070 okręgów wyborczych (najmniejszy podział administracyjny do celów wyborczych w Wielkiej Brytanii), z liczbą głosów na urlop i pozostanie w każdym z nich. Martin Rosenbaum obliczył pewne związki statystyczne między odsetkiem głosów zwolnionych na oddziale a niektórymi jego cechami społecznymi, ekonomicznymi i demograficznymi, korzystając z najnowszego spisu ludności w Wielkiej Brytanii, który przeprowadzono w 2011 r. Wykorzystał swoje dane dla klasy uniwersyteckiej , i to są dane, których użyjemy w tym przykładzie, po usunięciu niektórych zmiennych. W tabeli przedstawiono zmienne zawarte w danych

 

Kończąc tą sekcję wprowadzającą, chciałbym przedstawić trzy przykłady, które będziemy rozwijać w dalszej części. Pierwszym z nich jest przykład głosów w sprawie Brexitu, w którym wykorzystamy rzeczywiste dane dotyczące głosów w sprawie Brexitu, a dzięki statystykom opisowym i modelom liniowym spróbujemy zrozumieć dynamikę populacji, która stoi za wynikami. Jeśli nie jesteś zaznajomiony z Brexitem, to popularne określenie na przyszłe wyjście Wielkiej Brytanii z Unii Europejskiej po referendum, które odbyło się 23 czerwca 2016 r.

Drugi to przykład The Food Factory, w którym dowiesz się, jak symulować różnego rodzaju dane dla hipotetycznej firmy o nazwie The Food Factory, a także integrować rzeczywiste dane z innych źródeł (w tym przypadku opinie klientów), aby uzupełnić nasze symulacje . Dane zostaną wykorzystane do opracowania różnego rodzaju wizualizacji, analizy tekstu i prezentacji, które są aktualizowane automatycznie.

Trzecim i ostatnim z nich jest przykład systemu śledzenia kryptowalut, w którym opracujemy zorientowany obiektowo system, który będzie używany do pobierania danych cenowych w czasie rzeczywistym z rynków kryptowalut oraz ilości posiadanych przez nas aktywów kryptowalut. Następnie pokażemy, jak efektywnie obliczyć prostą średnią ruchomą przy użyciu technik optymalizacji wydajności, a na koniec pokażemy, jak tworzyć interaktywne aplikacje internetowe przy użyciu tylko R.

Na koniec przyjrzymy się pętlom while, które wykorzystują inny sposób zapętlania niż pętle for. W przypadku pętli for znamy liczbę elementów w obiekcie, których używamy do iteracji, więc z góry znamy liczbę iteracji, które zostaną wykonane. Jednak są chwile, w których nie znamy tej liczby przed rozpoczęciem iteracji, a zamiast tego będziemy iterować w oparciu o spełnienie pewnego warunku po każdej iteracji. Wtedy przydatne są pętle while Sposób działania pętli while polega na tym, że określamy warunek, tak jak w przypadku warunków if …else i jeśli warunek jest spełniony, przechodzimy do iteracji. Po zakończeniu iteracji ponownie sprawdzamy warunek i jeśli nadal jest prawdziwy, powtarzamy iterację i tak dalej. Zauważ, że w tym przypadku, jeśli chcemy zatrzymać się w pewnym momencie, musimy zmodyfikować elementy użyte w warunku tak, aby w pewnym momencie wyniósł FALSE. Możesz także użyć break i next wewnątrz pętli while. Poniższy przykład pokazuje, jak wydrukować wszystkie liczby całkowite od 1 do 10. Zauważ, że jeśli zaczynamy od 1 tak jak robimy, ale zamiast dodawać 1 po każdej iteracji, odejmujemy 1 lub nie zmieniamy didn’t nigdy nie przestanie iterować. Dlatego musisz być bardzo ostrożny podczas używania pętli while, ponieważ liczba iteracji może być nieskończona:

x <- 1

while (x <= 10) {

prit(x)

x<- x + 1

}

#> [1] 1

#> [1] 2

#> [1] 3

#> [1] 4

#> [1] 5

#> [1] 6

#> [1] 7

#> [1] 8

#> [1] 9

#> [1] 10

Jeśli chcesz wykonać nieskończoną pętlę, możesz użyć pętli while z wartością TRUE zamiast warunku. Jeśli nie dołączysz polecenia break, kod skutecznie zapewni nieskończoną pętlę i będzie się powtarzał, dopóki nie zostanie zatrzymany za pomocą polecenia klawiaturowego CTRL + C lub innego mechanizmu zatrzymywania w używanym IDE. Jednak w takich przypadkach czystsze jest użycie konstrukcji powtarzania, jak pokazano poniżej. Może się to wydawać sprzeczne z intuicją, ale są chwile, kiedy użycie nieskończonych pętli jest przydatne. W takich przypadkach masz zewnętrzny mechanizm używany do zatrzymania programu na podstawie warunku zewnętrznego względem R. następujący przykład spowoduje awarię sesji R:

# DO NOT ExECUTE THIS IT’s AN INFIITE LOOP

x <- 1

repeat {

print(x)

x <- x +1

}

#> [1] 1

#> [1] 2

#> [1] 3

#> [1] 4

#> [1] 5

#> [1] 5

…

Istnieją dwie ważne właściwości pętli for. Po pierwsze, wyniki nie są wypisywane wewnątrz pętli, chyba że jawnie wywołasz funkcję print(). Po drugie, zmienna indeksująca używana w pętli for będzie zmieniana po kolei po każdej iteracji. Ponadto, aby zatrzymać iterację, możesz użyć słowa kluczowego break, a aby przejść do następnej iteracji, możesz użyć następnego polecenia. W pierwszym przykładzie tworzymy wektor znaków o nazwie words i iterujemy przez każdy z jego elementów w kolejności, używając składni for (słowo w słowach). Spowoduje to pobranie pierwszego elementu z words, przypisanie go do word i przekazanie go przez wyrażenie zdefiniowane w bloku zdefiniowanym przez nawiasy klamrowe, które w tym przypadku wypisują słowo do konsoli, jako a także liczbę znaków w słowie. Po zakończeniu iteracji słowo zostanie zaktualizowane następnym słowem, a pętla będzie powtarzana w ten sposób, aż wszystkie słowa zostaną użyte:

words <- c(„Hello”, „there”, „dear”, „reader”)

for (word in words){

print(word)

print(nchar(word))

}

#> [1] “Hello”

#> [1] 5

#> [1] “there”

#> [1] 5

#> [1] “deare”

#> [1] 4

#> [1] “reader”

#> [1] 6

Ciekawe zachowanie można osiągnąć, używając zagnieżdżonych pętli for, które są  pętlami for wewnątrz innych pętli for. W tym przypadku obowiązuje ta sama logika, kiedy napotkamy pętlę for, wykonujemy ją aż do zakończenia. Rezultat takiego zachowania łatwiej jest zobaczyć, niż go wyjaśnić, więc spójrz na zachowanie następującego kodu:

for (i in 1:5) {

print(i)

for (j in 1:3) {

print(paste)(„    „ , j))

}

}

#> [1] 1

#> [1] “1”

#> [1] “2”

#> [1] “3”

#> [1] 2

#> [1] “1”

#> [1] “2”

#> [1] “3”

#> [1] 3

#> [1] “1”

#> [1] “2”

#> [1] “3”

#> [1] 4

#> [1] “1”

#> [1] “2”

#> [1] “3”

#> [1] 5

#> [1] “1”

#> [1] “2”

#> [1] “3”

Używanie takich zagnieżdżonych pętli for jest sposobem, w jaki ludzie wykonują operacje podobne do macierzy, gdy używają języków, które nie oferują operacji wektoryzowanych. Na szczęście możemy użyć składni przedstawionej w poprzednich sekcjach, aby wykonać te operacje bez konieczności samodzielnego używania zagnieżdżonych pętli for, co czasami może być trudne. Teraz zobaczymy, jak używać funkcji sapply() i lapply(), aby zastosować funkcję dla każdego elementu wektora. W tym przypadku wywołamy funkcję nchr() na każdym z elementów w wektorze słów, który utworzyliśmy wcześniej. Różnica między funkcjami sapply() i lapply() polega na tym, że pierwsza zwraca wektor, a druga zwraca listę. Na koniec zwróć uwagę, że jawne używanie którejkolwiek z tych funkcji nie jest konieczne, ponieważ, jak widzieliśmy wcześniej, funkcja nchar() jest już dla nas zwektoryzowana:

sapply(words, nchar)

#> Witam drogi czytelniku

#> 5 5 4 6

slapply(words, nchar)

#> [[1]]

#> [1] 5

#>

#> [[2]]

#> [1] 5

#>

#> [[3]]

#> [1] 4

#>

#> [[4]]

#> [1] 6

nchar(words)

#> [1] 5 5 4 6

Kiedy masz funkcję, która nie została wektoryzowana, jak nasza funkcja distance(). Nadal można go używać w sposób zwektoryzowany, korzystając z funkcji, o których właśnie wspomnieliśmy. W tym przypadku zastosujemy go do listy x, która zawiera trzy różne wektory numeryczne. Użyjemy funkcji lapply(), przekazując jej listę, po której nastąpi funkcja, którą chcemy zastosować do każdego z jej elementów (w tym przypadku distance(). Zwróć uwagę, że w przypadku, gdy funkcja, której używasz, otrzyma inne argumenty oprócz tego, który zostanie pobrany z x i który zostanie przekazany jako pierwszy argument do takiej funkcji, możesz przekazać je po nazwie funkcji, tak jak robimy to tutaj argumenty c(1,1,1) i l1_norm, które zostaną odebrane przez funkcję distance() jako argumenty y i norm, i pozostają ustalone dla wszystkich elementów listy x:

x <- list (c(1,2,3), c(4,5,6), c(7,8,9)

lapply(x ,distance ,c(1,1,1), l1_norm)

#> [[1]]

#> [1] 3

#>

#> [[2]]

#> [1] 12

#>

#> [[3]]

#> [1] 21

Jak wskazuje ich nazwa, if … else warunkowe sprawdzą warunek i jeśli zostanie oszacowany jako wartość TRUE, zostanie wybrana jedna ścieżka wykonania, ale jeśli warunek zostanie oceniony jako FALSE value, wybrana zostanie inna ścieżka wykonania i wykluczają się one wzajemnie. Aby pokazać, jak działają if … else warunki, zaprogramujemy tę samą funkcję distance(), której używaliśmy wcześniej, ale zamiast przekazywać jej trzeci argument w postaci funkcji , przekażemy jej ciąg znaków, który zostanie sprawdzony, aby zdecydować, której funkcji należy użyć. W ten sposób możesz porównać różne sposoby implementacji tej samej funkcjonalności. Jeśli przekażemy łańcuch 12 do argumentu norm, zostanie użyta funkcja 12_norm(), ale jeśli przepuszczony zostanie jakikolwiek inny ciąg, zostanie użyta 11_norm(). Zauważ, że używamy podwójnego operatora równości (==), aby sprawdzić równość. Nie myl tego z pojedynczym równa się, co oznacza przypisanie:

distance <- function(x,y = 0, norm „12”){

if (norm == „12”) {

return(12_norm(x,y))

} else [

return(11_norm(x,y))

}

}

a <- c(1,2,3)

b <- c(4,5,6)

distance(a,b)

#> 27

distance(a,b,”12”)

#> 27

distance(a,b,”12”)

#> 9

distance(a,b,”l1 will be also used in this case”)

#> 9

Jak widać w ostatnim wierszu poprzedniego przykładu, użycie warunków warunkowych w sposób nieregularny może wprowadzić potencjalne błędy, ponieważ w tym przypadku użyliśmy funkcji l1_norm(), nawet jeśli argument norm w ostatnie wywołanie funkcji nie miało żadnego sensu. Aby uniknąć takich sytuacji, możemy wprowadzić więcej warunków warunkowych, aby wyczerpać wszystkie prawidłowe możliwości i zgłosić błąd funkcją stop(), jeśli wykonywana jest gałąź else, co oznaczałoby, że nie podano żadnej ważnej opcji :

distance <- function(x,y = 0, norm = „12”){

if (norm == „12”) {

return(12_norm(x,y))

}else if (norm == „l1”){

return(l1_norm(x,y)

}else {

stop(„Inwvalid norm option”)

}

}

distance(a,b,”l1”_

#> [1] 9

distance(a,b, „this will produce an error”)

#> Błąd w distance (a, b, “spowoduje to błąd”):

#> Nieprawidłowa opcja norm

Czasami else część  if … else nie jest potrzebna. W takim przypadku możesz po prostu uniknąć umieszczania go, a R wykona gałąź if, jeśli warunek zostanie spełniony, i zignoruje go, jeśli nie jest. Istnieje wiele różnych sposobów generowania wartości logicznych, których można użyć w ramach kontroli if(). Na przykład, możesz określić opcjonalny argument z wartością domyślną NULL i sprawdzić, czy nie został on wysłany w wywołaniu funkcji, sprawdzając, czy odpowiednia zmienna nadal zawiera obiekt NULL w momencie sprawdzania, używając funkcji is.null(). Rzeczywisty warunek wyglądałby mniej więcej tak if(is.null(optional_argument)). Innym razem możesz otrzymać wektor logiczny i jeśli jedną z jego wartości jest TRUE, to chcesz wykonać fragment kodu, w takim przypadku możesz użyć czegoś takiego jak if(any(logical_vector)) jako warunek lub w przypadku, gdy wymagasz, aby wszystkie wartości w wektorze logicznym były TRUE do wykonania fragmentu kodu, możesz użyć czegoś takiego jak if(all(logical_vector)). Tę samą logikę można zastosować do funkcji samoopisowych nazwanych is.na() iis.nan().

Innym sposobem generowania tych wartości logicznych jest użycie operatorów porównania. Należą do nich mniej niż (<), mniejsze lub równe (<=), większe niż (>), większe lub równe (> =), dokładnie równe (co widzieliśmy, ==) i nie równe (! =). Wszystkie z nich mogą być używane do testowania liczb, a także znaków, w takim przypadku używany jest porządek alfanumeryczny. Ponadto wartości logiczne można łączyć między sobą, aby zapewnić bardziej złożone warunki. Na przykład! operator zaneguje logikę, co oznacza, że ​​jeśli !TRUE jest równe FALSE, a !FALSE jest równe TRUE. Innymi przykładami operatorów tego typu są operator OR, gdzie w przypadku, gdy którakolwiek z wartości logicznych to TRUE, wówczas całe wyrażenie daje w wyniku TRUE oraz operator AND, w którym wszystkie logiczne muszą mieć wartość TRUE ocenić na TRUE. Chociaż nie pokazujemy konkretnych przykładów informacji wymienionych w ostatnich dwóch akapitach, zobaczysz, że zostały one użyte w przykładach, które rozwiniemy w dalszej. Na koniec zwróć uwagę, że wektoryzowana postać warunku if…else jest dostępna w funkcji ifelse(). W poniższym kodzie używamy operatora modulo w warunku, który jest pierwszym argumentem funkcji, aby określić, które wartości są parzyste, w takim przypadku używamy gałęzi TRUE, która jest drugim argumentem, aby wskazać, że liczba całkowita jest parzysta, a które nie, w takim przypadku używamy gałęzi FALSE, która jest trzecim argumentem, aby wskazać, że liczba całkowita jest nieparzysta:

ifelse(c(1,2,3,4,5,6) %% 2 == 0, „parzyste”, „nieparzyste”

#> [1] “nieparzyste” “parzyste” “nieparzyste” “parzyste” “nieparzyste” “parzyste”

Ostatnim tematem, który powinniśmy omówić, jest wprowadzenie złożonej logiki za pomocą struktur sterujących. Kiedy piszę wprowadzenie złożonej logiki, nie mam na myśli sugestii, że jest to skomplikowane. Złożona logika odnosi się do kodu, który ma wiele możliwych ścieżek wykonania, ale w rzeczywistości jest dość prosty do zaimplementowania. Prawie każda operacja w R może być zapisana jako funkcja, a te funkcje można przekazać do innych funkcji, aby stworzyć bardzo złożone zachowanie. Jednak implementacja logiki w ten sposób nie zawsze jest wygodna, a użycie prostych struktur sterowania może być czasami lepszą opcją. Struktury kontrolne, którym przyjrzymy się, to if … else warunkowe, pętle for i pętle while. Istnieją również warunkowe przełączniki, które są bardzo podobne do warunkowych if … else warunkowych, ale nie będziemy ich przeglądać, ponieważ nie będziemy ich używać w naszych przykładach.