Wprowadzenie do optymalizacji
Do tej pory traktowaliśmy większość algorytmów jako częściowe czarne skrzynki, ponieważ skupiliśmy się na zrozumieniu danych wejściowych, których należy się spodziewać, i wyników, które otrzymasz. Zasadniczo potraktowaliśmy algorytmy uczenia maszynowego jako bibliotekę funkcji do wykonywania zadań prognozowania. W tej części przyjrzymy się niektórym technikom stosowanym do implementacji najbardziej podstawowych algorytmów uczenia maszynowego. Na początek przygotujemy funkcję dopasowania prostych modeli regresji liniowej za pomocą tylko jednego predyktora. Ten przykład pozwoli nam zmotywować ideę postrzegania aktu dopasowania modelu do danych jako problemu optymalizacji. Problemem optymalizacji jest ten, w którym mamy maszynę z kilkoma pokrętłami, które możemy obrócić, aby zmienić ustawienia maszyny i sposób pomiaru wydajności maszyny przy obecnych ustawieniach. Chcemy znaleźć najlepsze możliwe ustawienia, które będą maksymalizowały prosty pomiar wydajności maszyny. Ten punkt będzie nazywany optymalnym. Osiągnięcie go będzie nazywane optymalizacją. Kiedy już zrozumiemy, w jaki sposób działa optymalizacja, przystąpimy do naszego głównego zadania: zbudowania bardzo prostego systemu łamania kodu, który traktuje odszyfrowanie zaszyfrowanego tekstu jako problem optymalizacji. Ponieważ zamierzamy zbudować własną funkcję regresji liniowej, wróćmy do naszego standardowego przykładowego zestawu danych: wysokości i masy ludzi. Jak już zrobiliśmy, zakładamy, że możemy przewidzieć wagi, obliczając funkcję ich wysokości. W szczególności założymy, że działa funkcja liniowa, która wygląda następująco w R:
height.to.weight <- function(height, a, b)
{
return(a + b * height)
}
Wcześniej omawialiśmy szczegóły obliczania nachylenia przecięcia tej linii za pomocą funkcji lm. W tym przykładzie parametr a jest nachyleniem linii, a parametr b to punkt przecięcia, który mówi nam, ile powinna ważyć osoba o wysokości zero. Z tą funkcją w jaki sposób możemy zdecydować, które wartości a i b są najlepsze? W tym momencie pojawia się optymalizacja: chcemy najpierw zdefiniować miarę tego, jak dobrze nasza funkcja przewiduje wagi z wysokości, a następnie zmienić wartości a i b, aż przewidzimy tak dobrze, jak to możliwe. Jak to robimy? Cóż, już to wszystko dla nas robi. Ma prostą funkcję błędu, którą próbuje zoptymalizować, i znajduje najlepsze wartości dla a i b przy użyciu bardzo specyficznego algorytmu, który działa tylko dla zwykłej regresji liniowej. Po prostu uruchommy lm, aby zobaczyć jego preferowane wartości dla a i b :
heights.weights <- read.csv(‘data/01_heights_weights_genders.csv’)
coef(lm(Weight ~ Height, data = heights.weights))
#(Intercept) Height
#-350.737192 7.717288
Dlaczego są to rozsądne wybory dla a i b? Aby odpowiedzieć na to pytanie, musimy wiedzieć, jakiej funkcji błędu używa lm. Jak powiedzieliśmy pokrótce wcześniej, lm opiera się na pomiarze błędu zwanym „kwadratem błędu”, który działa w następujący sposób:
- Ustal wartości dla a i b.
- Biorąc pod uwagę wartość wysokości, zgadnij związaną z nią wagę.
- Weź prawdziwą wagę i odejmij przewidywaną wagę. Nazwij to błędem.
- Popraw błąd.
- Zsumuj kwadratowe błędy we wszystkich przykładach, aby uzyskać sumę kwadratów błędów.
Do interpretacji zwykle bierzemy średnią, a nie sumę, i oblicz pierwiastki kwadratowe. Ale do optymalizacji nic z tego nie jest naprawdę konieczne, więc możemy zaoszczędzić trochę czasu obliczeniowego, po prostu obliczając sumę kwadratów błędów. Dwa ostatnie kroki są ściśle powiązane; gdybyśmy nie sumowali błędów dla każdego punktu danych razem, kwadratowanie nie byłoby pomocne. Wyrównanie jest niezbędne właśnie dlatego, że sumowanie wszystkich błędów pierwotnych razem dałoby nam zero błędów całkowitych. Pokazanie, że jest to zawsze prawda, nie jest trudne, ale wymaga tego rodzaju algebry, której próbujemy uniknąć. Przejdźmy przez kod, który implementuje to podejście:
squared.error <- function(heights.weights, a, b)
{
predictions <- with(heights.weights, height.to.weight(Height, a, b))
errors <- with(heights.weights, Weight – predictions)
return(sum(errors ^ 2))
}
Przeprowadźmy ocenę squared.error przy niektórych określonych wartościach a i b, aby zorientować się, jak to działa
for (a in seq(-1, 1, by = 1))
{
for (b in seq(-1, 1, by = 1))
{
print(squared.error(heights.weights, a, b))
}
}
Wyniki :
a : b : Błąd kwadratu
-1 : -1 : 536271759
-1 : 0 : 274177183
-1 : 1 :100471706
0 : -1 : 531705601
0 : 0 : 270938376
0 : 1 : 98560250
1 : -1 : 527159442
1 : 0 : 267719569
1 : 1 : 96668794
Jak widać, niektóre wartości a i b dają znacznie niższe wartości dla squared.error niż inne. Oznacza to, że naprawdę chcemy znaleźć najlepsze wartości dla a i b teraz, gdy mamy znaczącą funkcję błędu, która mówi nam coś o naszej zdolności do przewidywania. To pierwsza część naszego problemu z optymalizacją: skonfiguruj dane, które możemy następnie zminimalizować lub zmaksymalizować. Ta metryka jest zwykle nazywana naszą funkcją celu. Problem optymalizacji staje się wówczas problemem znalezienia najlepszych wartości dla a i b, aby funkcja celu była tak mała lub tak duża, jak to możliwe. Jedno oczywiste podejście nazywa się wyszukiwaniem siatki: oblicz tabelę taką jak ta, którą właśnie pokazaliśmy dla wystarczająco dużego zakresu wartości ai b, a następnie wybierz wiersz o najniższej wartości squared.error. Takie podejście zawsze zapewnia najlepszą wartość w przeszukiwanej siatce, więc nie jest to nieracjonalne podejście. Ale są z tym poważne problemy:
- Jak blisko powinny się znajdować wartości używane do definiowania siatki? Czy a powinno mieć wartości 0, 1, 2, 3? A może powinny być wartości 0, 0,001, 0,002, 0,003? Innymi słowy, jaka jest właściwa rozdzielczość, przy której powinniśmy przeprowadzić nasze wyszukiwanie? Odpowiedź na to pytanie wymaga oceny obu siatek i sprawdzenia, które informacje są bardziej pouczające, co jest kosztowne obliczeniowo i skutecznie wprowadza kolejny drugi problem optymalizacji, w którym optymalizujesz rozmiar używanej siatki. Na tej drodze leży szaleństwo nieskończonej pętli.
- Jeśli chcesz ocenić tę siatkę w 10 punktach na parametr dla 2 parametrów, musisz zbudować tabelę zawierającą 100 wpisów. Ale jeśli chcesz to ocenić tę siatkę w 10 punktach na parametr dla 100 parametrów, musisz zbudować tabelę z 10 ^ 100 pozycji. Problem wzrostu wykładniczego jest tak powszechny w uczeniu maszynowym, że nazywa się go Klątwą Wymiarowości.
Ponieważ chcemy być w stanie zastosować regresję liniową z setkami, a nawet tysiącami danych wejściowych, wyszukiwanie siatki jest dobre jako algorytm optymalizacji. Więc co możemy zrobić? Na szczęście dla nas informatycy i matematycy zastanawiali się nad problemem optymalizacji przez długi czas i zbudował duży zestaw gotowych algorytmów optymalizacji, których można użyć. W R zwykle powinieneś wykonać pierwsze przejście przy problemie z optymalizacją za pomocą funkcji optim, która zapewnia czarną skrzynkę, która implementuje wiele najpopularniejszych algorytmów optymalizacji. Aby pokazać, jak działa optim, wykorzystamy go, aby pasował do naszego modelu regresji liniowej. Mamy nadzieję, że spowoduje to wygenerowanie wartości dla a i b podobnych do tych wytworzonych przez lm:
optim(c(0, 0),
function (x)
{
squared.error(heights.weights, x[1], x[2])
})
#$par
#[1] -350.786736 7.718158
#
#$value
#[1] 1492936
#
#$counts
#function gradient
# 111 NA
#
#$convergence
#[1] 0
#
#$message
#NULL
Jak pokazuje przykład, optim przyjmuje kilka różnych argumentów. Najpierw musisz podać wektor liczbowy punktów początkowych dla parametrów, które próbujesz zoptymalizować; w tym przypadku mówimy, że a i b powinny mieć domyślnie wektor c (0, 0). Następnie musisz przekazać funkcję do optymalizacji, która spodziewa się otrzymać wektor, który nazwaliśmy x, który zawiera wszystkie parametry, które chcesz zoptymalizować. Ponieważ zwykle wolimy pisać funkcje z wieloma nazwanymi parametrami, lubimy zawijać naszą funkcję błędu w anonimowej funkcji, która bierze tylko argument x, który następnie dzielimy na naszą podstawową funkcję błędu. W tym przykładzie możesz zobaczyć, jak się opakowaliśmy squared.error. Uruchomienie tego wywołania funkcji optim daje nam odpowiednio wartości a i b, jako wartości par. A te wartości są bardzo zbliżone do tych wytwarzanych przez lm, co sugeruje, że optim działa. W praktyce lm wykorzystuje algorytm, który jest znacznie bardziej specyficzny dla regresji liniowej niż nasze wezwanie do optymalizacji, co sprawia, że wyniki są bardziej precyzyjne niż te generowane przez optim. Jeśli masz zamiar poradzić sobie z własnymi problemami, optym jest o wiele lepszy do pracy, ponieważ można go używać z modelami innymi niż regresja liniowa. Inne wyniki, które otrzymujemy z optim są czasami mniej interesujące. Pierwszą, którą pokazaliśmy, jest wartość, która mówi nam o wartości kwadratu błędu oszacowanego przy parametrach, które optymalne twierdzą, że są najlepsze. Następnie wartość zliczeń mówi nam, ile razy optymalnie ocenił funkcję główną (tutaj nazywaną funkcją) i gradient (tutaj nazywany gradientem), który jest opcjonalnym argumentem, który można przekazać, jeśli znasz wystarczającą liczbę rachunku różniczkowego do obliczenia gradientu główna funkcja. Jeśli termin „gradient” nic dla ciebie nie znaczy, nie martw się. Nie lubimy ręcznie obliczać gradientów, dlatego zwykle pozwalamy optymalizować na magię bez określania wartości opcjonalnego argumentu gradientu. Jak dotąd wszystko ułożyło się całkiem dobrze, choć przebieg może się różnić.
Jak pokazuje przykład, optim przyjmuje kilka różnych argumentów. Najpierw musisz podać wektor liczbowy punktów początkowych dla parametrów, które próbujesz zoptymalizować; w tym przypadku mówimy, że aib powinny mieć domyślnie wektor c (0, 0). Następnie musisz przekazać funkcję do optymalizacji, która spodziewa się otrzymać wektor, który nazwaliśmy x, który zawiera wszystkie parametry, które chcesz zoptymalizować. Ponieważ zwykle wolimy pisać funkcje z wieloma nazwanymi parametrami, lubimy zawijać naszą funkcję błędu w anonimowej funkcji, która bierze tylko argument x, który następnie dzielimy na naszą podstawową funkcję błędu. W tym przykładzie możesz zobaczyć, jak się opakowaliśmy squared.error. Uruchomienie tego wywołania funkcji optim daje nam odpowiednio wartości a i b, jako wartości par. A te wartości są bardzo zbliżone do tych wytwarzanych przez lm, co sugeruje, że optim działa. W praktyce lm wykorzystuje algorytm, który jest znacznie bardziej specyficzny dla regresji liniowej niż nasze wezwanie do optymalizacji, co sprawia, że wyniki są bardziej precyzyjne niż te generowane przez optim. Jeśli masz zamiar poradzić sobie z własnymi problemami, optim jest o wiele lepszy do pracy, ponieważ można go używać z modelami innymi niż regresja liniowa. Inne wyniki, które otrzymujemy z optim są czasami mniej interesujące. Pierwszą, którą pokazaliśmy, jest wartość, która mówi nam o wartości kwadratu błędu oszacowanego przy parametrach, które optymalne twierdzą, że są najlepsze. Następnie wartość zliczeń mówi nam, ile razy optymalnie ocenił funkcję główną (tutaj nazywaną funkcją) i gradient (tutaj nazywany gradientem), który jest opcjonalnym argumentem, który można przekazać, jeśli znasz wystarczającą liczbę rachunku różniczkowego do obliczenia gradientu główna funkcja.
Jeśli termin „gradient” nic dla ciebie nie znaczy, nie martw się. Nie lubimy ręcznie obliczać gradientów, dlatego zwykle pozwalamy optymalizować na magię bez określania wartości opcjonalnego argumentu gradientu. Jak dotąd wszystko ułożyło się całkiem dobrze, choć przebieg może się różnić.
Następną wartością jest konwergencja, która mówi nam, czy optim znalazł zestaw parametrów, które według niego są najlepsze z możliwych. Jeśli wszystko poszło dobrze, zobaczysz 0. Sprawdź dokumentację, aby uzyskać optymalną interpretację różnych kodów błędów, które możesz uzyskać, gdy wynik nie jest równy 0. Na koniec wartość komunikatu mówi nam, czy stało się coś, co musimy wiedzieć o. Ogólnie rzecz biorąc, optim opiera się na wielu sprytnych pomysłach z rachunku różniczkowego, które pomagają nam przeprowadzić optymalizację. Ponieważ jest to dość skomplikowane matematycznie, w ogóle nie wdajemy się w wewnętrzne działania programu Optim. Ale ogólny duch tego, co robi optim, jest bardzo prosty do wyrażenia graficznego. Wyobraź sobie, że chciałeś znaleźć najlepszą wartość a po tym, jak zdecydowałeś, że b musi wynosić 0. Możesz obliczyć błąd do kwadratu, gdy zmieniasz tylko za pomocą następującego kodu:
a.error <- function(a)
{
return(squared.error(heights.weights, a, 0))
}
Aby dowiedzieć się, gdzie jest najlepsza wartość a, możesz wykreślić kwadratowy błąd jako funkcję użycia funkcji krzywej w R, która oceni funkcję lub wyrażenie na zestawie wielu wartości zmiennej x, a następnie wykreśl wyniki tej funkcji lub wartość wyrażenia. W poniższym przykładzie oceniliśmy błąd a. Na wielu wartościach x i z powodu dziwactwa w ocenie wyrażeń R. musieliśmy użyć sapply, aby wszystko działało.
curve(sapply(x, function (a) {a.error(a)}), from = -1000, to = 1000)
Patrząc na rysunek
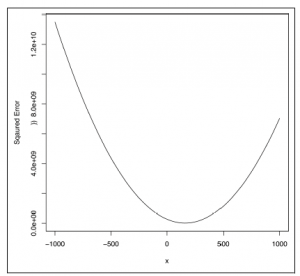
wydaje się, że istnieje jedna wartość dla tego, co najlepsze, a każda wartość, która oddala się od tej wartości dla a, jest gorsza. Kiedy tak się dzieje, mówimy, że istnieje globalne optimum. W takich przypadkach optim może użyć kształtu funkcji błędu kwadratu, aby ustalić kierunek, w którym należy podążać po oszacowaniu funkcji błędu na pojedynczej wartości a; Wykorzystanie tych lokalnych informacji, aby dowiedzieć się czegoś o globalnej strukturze twojego problemu, pozwala optymalnie bardzo szybko osiągnąć optymalne. Aby lepiej zrozumieć problem pełnej regresji, musimy również przyjrzeć się reakcji funkcji błędu po zmianie b:
b.error <- function(b)
{
return(squared.error(heights.weights, 0, b))
}
curve(sapply(x, function (b) {b.error(b)}), from = -1000, to = 1000)
Patrząc na rysunek 7-2, funkcja błędu wygląda tak, jakby miała również globalne optimum dla b.
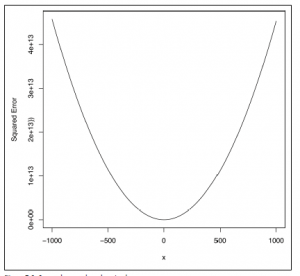
W połączeniu z dowodami, że istnieje globalne optimum dla a, sugeruje to, że optymalizator powinien mieć możliwość znalezienia jednej najlepszej wartości zarówno dla a, jak i b, która minimalizuje naszą funkcję błędu.
Mówiąc bardziej ogólnie, możemy powiedzieć, że optym działa, ponieważ może wyszukiwać doliny tych wykresów we wszystkich parametrach jednocześnie za pomocą rachunku różniczkowego. Działa szybciej niż wyszukiwanie siatki, ponieważ może wykorzystywać informacje o punkcie, który rozważa obecnie, aby wnioskować coś o punktach w pobliżu . To pozwala mu zdecydować, w którym kierunku powinien zmierzać, aby poprawić swoją wydajność. To zachowanie adaptacyjne czyni go znacznie bardziej wydajnym niż wyszukiwanie w siatce