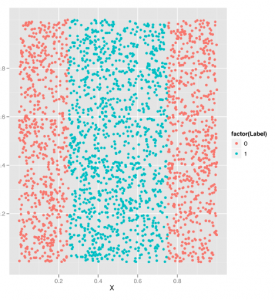
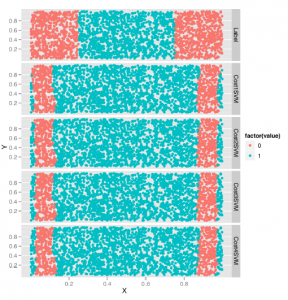
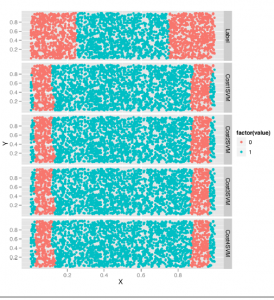
Ponieważ wiemy, jak korzystać z SVM, regresji logistycznej i kNN, porównajmy ich wydajność w zbiorze danych SpamAssassin, nad którym pracowaliśmy we wcześniejszych częściach. Eksperymentowanie z wieloma algorytmami jest dobrym nawykiem do rozwijania podczas pracy z danymi ze świata rzeczywistego ponieważ często nie będziesz w stanie z góry wiedzieć, który algorytm będzie działał najlepiej z Twoim zestawem danych. Jedną z głównych umiejętności, która odróżnia najbardziej doświadczonych ludzi w uczeniu maszynowym od tych, którzy dopiero zaczynają go używać, jest umiejętność poznania struktury problemu, gdy określony algorytm nie działa dobrze. Najlepszym sposobem na zbudowanie tej intuicji jest zastosowanie wszystkich standardowych algorytmów do każdego napotkanego problemu, dopóki nie zorientujesz się, kiedy się nie powiedzie. Pierwszym krokiem jest po prostu załadowanie naszych danych i odpowiednie ich wstępne przetworzenie. Ponieważ było to wcześniej zrobione szczegółowo, pomińmy kilka kroków i po prostu załadujemy macierz dokumentów z dysku za pomocą funkcji ładowania w R, która czyta w formacie binarnym, który może być używany do zapisywania obiektów R na dysku w celu przechowywania długoterminowego. Następnie podzielimy zestaw treningowy / zestaw testowy i odrzucimy nieprzetworzony zestaw danych za pomocą funkcji rm, która pozwala nam usunąć obiekt z pamięci:
load(‘data/dtm.RData’)
set.seed(1)
training.indices <- sort(sample(1:nrow(dtm), round(0.5 * nrow(dtm))))
test.indices <- which(! 1:nrow(dtm) %in% training.indices)
train.x <- dtm[training.indices, 3:ncol(dtm)]
train.y <- dtm[training.indices, 1]
test.x <- dtm[test.indices, 3:ncol(dtm)]
test.y <- dtm[test.indices, 1]
rm(dtm)
Teraz, gdy mamy zestaw danych w pamięci, możemy od razu przejść do przodu i dopasować regaryzowaną regresję logistyczną za pomocą glmnet:
library(‘glmnet’)
regularized.logit.fit <- glmnet(train.x, train.y, family = c(‘binomial’))
Oczywiście pozostawia to nam dużą elastyczność, dlatego chcielibyśmy porównać różne ustawienia hiperparametru lambda, aby zobaczyć, która daje nam najlepszą wydajność. Aby szybko przejść przez ten przykład, trochę oszukujemy i przetestujemy ustawienia hiperparametrów w zestawie testowym, zamiast powtarzać podziały danych treningowych. Jeśli rygorystycznie testujesz modele, nie powinieneś robić tego rodzaju uproszczenia, ale pozostawimy czyste tuningowanie lambda jako ćwiczenie, które możesz wykonać samodzielnie. Na razie wypróbujemy wszystkie wartości zaproponowane przez glmnet i zobaczymy, które wyniki są najlepsze w zestawie testowym:
lambdas <- regularized.logit.fit$lambda
performance <- data.frame()
for (lambda in lambdas)
{
predictions <- predict(regularized.logit.fit, test.x, s = lambda)
predictions <- as.numeric(predictions > 0)
mse <- mean(predictions != test.y)
performance <- rbind(performance, data.frame(Lambda = lambda, MSE = mse))
}
ggplot(performance, aes(x = Lambda, y = MSE)) +
geom_point() +
scale_x_log10()
Patrząc na Rysunek , widzimy całkiem wyraźny obszar wartości dla lambda, który daje najniższy możliwy poziom błędu.
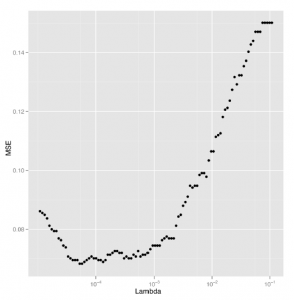
Aby znaleźć najlepszą wartość dla naszej ostatecznej analizy, możemy następnie zastosować proste indeksowanie i funkcję min:
best.lambda <- with(performance, max(Lambda[which(MSE == min(MSE))]))
W tym przypadku istnieją dwie różne wartości lambda, które dają identyczną wydajność, więc wyodrębniamy większą z nich za pomocą funkcji max. Wybieramy większą wartość, ponieważ jest to ta, dla której zastosowano większą regularyzację. Następnie możemy obliczyć MSE dla naszego modelu logistycznego, używając tej najlepszej wartości dla lambda:
mse <- with(subset(performance, Lambda == best.lambda), MSE)
mse
#[1] 0.06830769
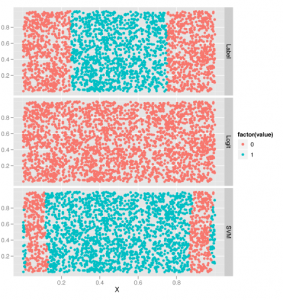
Widzimy, że stosowanie regularnej regresji logistycznej, która wymaga tylko niewielkiej ilości dostrajania hiperparametrów, błędnie klasyfikuje tylko 6% wszystkich wiadomości e-mail w naszym zestawie testowym. Chcielibyśmy jednak zobaczyć, jak inne metody radzą sobie z podobną ilością pracy, abyśmy mogli zdecydować, czy powinniśmy stosować regresję logistyczną, SVM czy kNN. Z tego powodu zacznijmy od dopasowania liniowego SVM jądra, aby zobaczyć, jak to się ma do regresji logistycznej:
library(‘e1071’)
linear.svm.fit <- svm(train.x, train.y, kernel = ‘linear’)
Montaż dużego jądra SVM jest nieco powolny przy tym dużym zestawie danych. Z tego powodu będziemy nieco niesprawiedliwi wobec SVM i po prostu użyjemy domyślnych ustawień hiperparametrów. Podobnie jak w przypadku wybierania idealnego hiperparametru do regresji logistycznej poprzez ocenę wydajności naszego zestawu testowego, to użycie domyślnych wartości hiperparametrów nie jest idealne, ale jest również regularnym zjawiskiem w literaturze dotyczącej uczenia maszynowego. Porównując modele, należy pamiętać, że jedną z rzeczy, które widzisz w wynikach, jest po prostu miara tego, jak ciężko pracowałeś, aby dopasować każdy model do danych. Jeśli poświęcasz więcej czasu na dostrajanie jednego modelu od drugiego, różnice w wydajności mogą częściowo wynikać z ich odmiennej struktury, ale z różnych poziomów wysiłku, który w nie zainwestowałeś. Wiedząc o tym, ślepo posuwamy się naprzód i oceniamy wydajność SVM liniowego jądra na podstawie naszych danych testowych:
predictions <- predict(linear.svm.fit, test.x)
predictions <- as.numeric(predictions > 0)
mse <- mean(predictions != test.y)
mse
#0.128
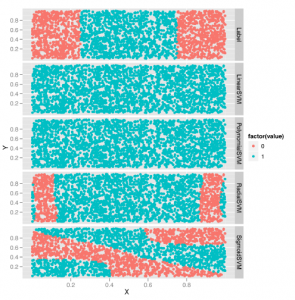
Widzimy, że otrzymujemy 12% poziom błędu, który jest dwukrotnie wyższy niż w przypadku modelu regresji logistycznej. Aby lepiej zrozumieć rzeczywiste granice SVM jądra liniowego, powinieneś eksperymentować z manipulacją hiperparametrem kosztów w celu znalezienia jego idealnej wartości przed oszacowaniem poziomu błędu dla SVM jądra liniowego. Ale na razie będziemy trzymać się wyników, które już mamy dla liniowego SVM jądra i przejść do radialnego SVM jądra, aby zobaczyć, jak bardzo jądro zmienia wyniki więc mamy do czynienia z tym praktycznym problemem, którego nie możemy wizualizować w ten sam sposób, w jaki moglibyśmy wizualizować problem zabawki na początku tego rozdziału:
radial.svm.fit <- svm(train.x, train.y, kernel = ‘radial’)
predictions <- predict(radial.svm.fit, test.x)
predictions <- as.numeric(predictions > 0)
mse <- mean(predictions != test.y)
mse
#[1] 0.1421538
Nieco zaskakujące jest to, że jądro promieniowe działa trochę gorzej na tym zestawie danych niż jądro liniowe, co jest przeciwieństwem tego, co widzieliśmy na przykładzie danych nieliniowych. A to przykład szerszej lekcji, którą przyswoisz sobie z większym doświadczeniem w pracy z danymi: idealny model twojego problemu zależy od struktury twoich danych. W tym przypadku gorsza wydajność radialnego jądra SVM sugeruje, że idealna granica decyzji dla tego problemu może być naprawdę liniowa. Jest to również wspierane przez fakt, że widzieliśmy już, że regresja logistyczna bije zarówno SVM jądra liniowego, jak i promieniowego. Tego rodzaju obserwacje są najciekawsze, jakie możemy przeprowadzić porównując algorytmy na ustalonym zbiorze danych, ponieważ dowiadujemy się czegoś o prawdziwej strukturze danych na podstawie niewłaściwego dopasowania naszych modeli. Zanim jednak przestaniemy dopasowywać modele i zdecydujemy się pozostać przy regresji logistycznej, spróbujmy metody, która najlepiej działa z danymi nieliniowymi: kNN. Tutaj dopasowujemy kNN przy użyciu 50 sąsiadów dla każdej prognozy:
library(‘class’)
knn.fit <- knn(train.x, test.x, train.y, k = 50)
predictions <- as.numeric(as.character(knn.fit))
mse <- mean(predictions != test.y)
mse
#[1] 0.1396923
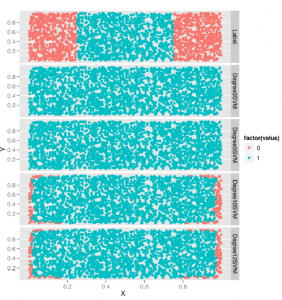
Jak widzimy, otrzymujemy 14% błąd z kNN, co jest kolejnym dowodem, że modele liniowe są lepsze do klasyfikowania spamu niż modele nieliniowe. A ponieważ kNN nie zajmuje tak dużo czasu, aby zmieścić się w tym zestawie danych, spróbujemy również kilka wartości dla k, aby zobaczyć, który działa najlepiej:
performance <- data.frame()
for (k in seq(5, 50, by = 5))
{
knn.fit <- knn(train.x, test.x, train.y, k = k)
predictions <- as.numeric(as.character(knn.fit))
mse <- mean(predictions != test.y)
performance <- rbind(performance, data.frame(K = k, MSE = mse))
}
best.k <- with(performance, K[which(MSE == min(MSE))])
best.mse <- with(subset(performance, K == best.k), MSE)
best.mse
#[1] 0.09169231
Dzięki tuningowi widzimy, że możemy uzyskać współczynnik błędu 9% z kNN. Jest to połowa drogi między wydajnością, jaką zaobserwowaliśmy dla maszyn SVM, a regresją logistyczną, co można potwierdzić, przeglądając tabelę 12-1, która zestawia wskaźniki błędów, które uzyskaliśmy z każdym z czterech algorytmów zastosowanych w tym zestawie danych spamu .
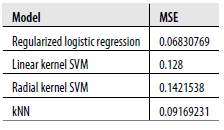
Ostatecznie wydaje się, że najlepszym rozwiązaniem tego problemu jest regresja logistyczna z dostrojonym hiperparametrem do regularyzacji. I to właściwie rozsądny wniosek, ponieważ wszystkie filtry antyspamowe o dużej mocy przeszły na regresję logistyczną i porzuciłem podejście Naive Bayes, które opisaliśmy wcześniej. Z przyczyn, które nie są dla nas całkowicie jasne, regresja logistyczna po prostu działa lepiej w przypadku tego rodzaju problemu. Jakie szersze lekcje powinieneś wyciągnąć z tego przykładu? Mamy nadzieję, że odejdziesz z myślą o kilku lekcjach: (1) zawsze powinieneś wypróbować wiele algorytmów na dowolnym praktycznym zbiorze danych, szczególnie dlatego, że tak łatwo jest eksperymentować z R; (2) rodzaje algorytmów, które działają najlepiej, są specyficzne dla problemu; oraz (3) na jakość wyników uzyskanych z modelu ma wpływ struktura danych, a także ilość pracy, jaką chcesz poświęcić na ustawianie hiperparametrów, więc nie unikaj kroku dostrajania hiperparametrów, jeśli chcę uzyskać dobre wyniki. Aby udoskonalić te lekcje w domu, zachęcamy do powrotu do czterech modeli, które pasowaliśmy w tym rozdziale i systematycznego ustawiania hiperparametrów za pomocą powtarzanych podziałów danych treningowych. Następnie zachęcamy do wypróbowania wielomianu i sigmoidu jądra, które zaniedbaliśmy podczas pracy z danymi spamu. Jeśli zrobisz obie te rzeczy, zyskasz duże doświadczenie w zakresie dopasowywania skomplikowanych modeli do rzeczywistych danych i nauczysz się doceniać, jak odmiennie modele pokazaliśmy ci w tym tekście może działać na stałym zestawie danych. W związku z tym doszliśmy do końca ostatniego rozdziału i książki jako całości. Mamy nadzieję, że odkryłeś piękno uczenia maszynowego i doceniłeś szerokie pomysły, które pojawiają się wielokrotnie, gdy próbujesz budować predykcyjne modele danych. Najlepszymi praktykami uczenia maszynowego są ci posiadający zarówno doświadczenie praktyczne, jak i teoretyczne, dlatego zachęcamy do wyjścia i rozwoju obu. Po drodze baw się dobrze podczas hakowania danych. Masz wiele zaawansowanych narzędzi, więc zastosuj je do interesujących Cię pytań!